AUTHORS:
Note
Unlike in PARI/GP, class group computations in Sage do not by default assume the Generalized Riemann Hypothesis. To do class groups computations not provably correctly you must often pass the flag proof=False to functions or call the function proof.number_field(False). It can easily take 1000’s of times longer to do computations with proof=True (the default).
This example follows one in the Magma reference manual:
sage: K.<y> = NumberField(x^4 - 420*x^2 + 40000)
sage: z = y^5/11; z
420/11*y^3 - 40000/11*y
sage: R.<y> = PolynomialRing(K)
sage: f = y^2 + y + 1
sage: L.<a> = K.extension(f); L
Number Field in a with defining polynomial y^2 + y + 1 over its base field
sage: KL.<b> = NumberField([x^4 - 420*x^2 + 40000, x^2 + x + 1]); KL
Number Field in b0 with defining polynomial x^4 - 420*x^2 + 40000 over its base field
We do some arithmetic in a tower of relative number fields:
sage: K.<cuberoot2> = NumberField(x^3 - 2)
sage: L.<cuberoot3> = K.extension(x^3 - 3)
sage: S.<sqrt2> = L.extension(x^2 - 2)
sage: S
Number Field in sqrt2 with defining polynomial x^2 - 2 over its base field
sage: sqrt2 * cuberoot3
cuberoot3*sqrt2
sage: (sqrt2 + cuberoot3)^5
(20*cuberoot3^2 + 15*cuberoot3 + 4)*sqrt2 + 3*cuberoot3^2 + 20*cuberoot3 + 60
sage: cuberoot2 + cuberoot3
cuberoot3 + cuberoot2
sage: cuberoot2 + cuberoot3 + sqrt2
sqrt2 + cuberoot3 + cuberoot2
sage: (cuberoot2 + cuberoot3 + sqrt2)^2
(2*cuberoot3 + 2*cuberoot2)*sqrt2 + cuberoot3^2 + 2*cuberoot2*cuberoot3 + cuberoot2^2 + 2
sage: cuberoot2 + sqrt2
sqrt2 + cuberoot2
sage: a = S(cuberoot2); a
cuberoot2
sage: a.parent()
Number Field in sqrt2 with defining polynomial x^2 - 2 over its base field
Warning
Doing arithmetic in towers of relative fields that depends on canonical coercions is currently VERY SLOW. It is much better to explicitly coerce all elements into a common field, then do arithmetic with them there (which is quite fast).
TESTS:
sage: y = polygen(QQ,'y'); K.<beta> = NumberField([y^3 - 3, y^2 - 2])
sage: K(y^10)
27*beta0
sage: beta^10
27*beta0
Return the n-th cyclotomic field, where n is a positive integer.
INPUT:
EXAMPLES: We create the 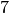 th cyclotomic field
th cyclotomic field
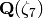 with the default generator name.
with the default generator name.
sage: k = CyclotomicField(7); k
Cyclotomic Field of order 7 and degree 6
sage: k.gen()
zeta7
The default embedding sends the generator to the complex primitive
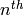 root of unity of least argument.
root of unity of least argument.
sage: CC(k.gen())
0.623489801858734 + 0.781831482468030*I
Cyclotomic fields are of a special type.
sage: type(k)
<class 'sage.rings.number_field.number_field.NumberField_cyclotomic_with_category'>
We can specify a different generator name as follows.
sage: k.<z7> = CyclotomicField(7); k
Cyclotomic Field of order 7 and degree 6
sage: k.gen()
z7
The  must be an integer.
must be an integer.
sage: CyclotomicField(3/2)
...
TypeError: no conversion of this rational to integer
The degree must be positive.
sage: CyclotomicField(0)
...
ValueError: n (=0) must be a positive integer
The special case 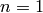 does not return the rational
numbers:
does not return the rational
numbers:
sage: CyclotomicField(1)
Cyclotomic Field of order 1 and degree 1
Due to their default embedding into 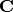 ,
cyclotomic number fields are all compatible.
,
cyclotomic number fields are all compatible.
sage: cf30 = CyclotomicField(30)
sage: cf5 = CyclotomicField(5)
sage: cf3 = CyclotomicField(3)
sage: cf30.gen() + cf5.gen() + cf3.gen()
zeta30^6 + zeta30^5 + zeta30 - 1
sage: cf6 = CyclotomicField(6) ; z6 = cf6.0
sage: cf3 = CyclotomicField(3) ; z3 = cf3.0
sage: cf3(z6)
zeta3 + 1
sage: cf6(z3)
zeta6 - 1
sage: cf9 = CyclotomicField(9) ; z9 = cf9.0
sage: cf18 = CyclotomicField(18) ; z18 = cf18.0
sage: cf18(z9)
zeta18^2
sage: cf9(z18)
-zeta9^5
sage: cf18(z3)
zeta18^3 - 1
sage: cf18(z6)
zeta18^3
sage: cf18(z6)**2
zeta18^3 - 1
sage: cf9(z3)
zeta9^3
Return the number field defined by the given irreducible
polynomial and with variable with the given name. If check is True
(the default), also verify that the defining polynomial is
irreducible and over  .
.
INPUT:
 or a number
field, or a list of polynomials.
or a number
field, or a list of polynomials.EXAMPLES:
sage: z = QQ['z'].0
sage: K = NumberField(z^2 - 2,'s'); K
Number Field in s with defining polynomial z^2 - 2
sage: s = K.0; s
s
sage: s*s
2
sage: s^2
2
Constructing a relative number field:
sage: K.<a> = NumberField(x^2 - 2)
sage: R.<t> = K[]
sage: L.<b> = K.extension(t^3+t+a); L
Number Field in b with defining polynomial t^3 + t + a over its base field
sage: L.absolute_field('c')
Number Field in c with defining polynomial x^6 + 2*x^4 + x^2 - 2
sage: a*b
a*b
sage: L(a)
a
sage: L.lift_to_base(b^3 + b)
-a
Constructing another number field:
sage: k.<i> = NumberField(x^2 + 1)
sage: R.<z> = k[]
sage: m.<j> = NumberField(z^3 + i*z + 3)
sage: m
Number Field in j with defining polynomial z^3 + i*z + 3 over its base field
Number fields are globally unique:
sage: K.<a>= NumberField(x^3-5)
sage: a^3
5
sage: L.<a>= NumberField(x^3-5)
sage: K is L
True
Having different defining polynomials makes the fields different:
sage: x = polygen(QQ, 'x'); y = polygen(QQ, 'y')
sage: k.<a> = NumberField(x^2 + 3)
sage: m.<a> = NumberField(y^2 + 3)
sage: k
Number Field in a with defining polynomial x^2 + 3
sage: m
Number Field in a with defining polynomial y^2 + 3
One can also define number fields with specified embeddings, may be used for arithmetic and deduce relations with other number fields which would not be valid for an abstract number field:
sage: K.<a> = NumberField(x^3-2, embedding=1.2)
sage: RR.coerce_map_from(K)
Composite map:
From: Number Field in a with defining polynomial x^3 - 2
To: Real Field with 53 bits of precision
Defn: Generic morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Real Lazy Field
Defn: a -> 1.259921049894873?
then
Conversion via _mpfr_ method map:
From: Real Lazy Field
To: Real Field with 53 bits of precision
sage: RR(a)
1.25992104989487
sage: 1.1 + a
2.35992104989487
sage: b = 1/(a+1); b
1/3*a^2 - 1/3*a + 1/3
sage: RR(b)
0.442493334024442
sage: L.<b> = NumberField(x^6-2, embedding=1.1)
sage: L(a)
b^2
sage: a + b
b^2 + b
Note that the image only needs to be specified to enough precision to distinguish roots, and is exactly computed to any needed precision:
sage: RealField(200)(a)
1.2599210498948731647672106072782283505702514647015079800820
One can embed into any other field:
sage: K.<a> = NumberField(x^3-2, embedding=CC.gen()-0.6)
sage: CC(a)
-0.629960524947436 + 1.09112363597172*I
sage: L = Qp(5)
sage: f = polygen(L)^3 - 2
sage: K.<a> = NumberField(x^3-2, embedding=f.roots()[0][0])
sage: a + L(1)
4 + 2*5^2 + 2*5^3 + 3*5^4 + 5^5 + 4*5^6 + 2*5^8 + 3*5^9 + 4*5^12 + 4*5^14 + 4*5^15 + 3*5^16 + 5^17 + 5^18 + 2*5^19 + O(5^20)
sage: L.<b> = NumberField(x^6-x^2+1/10, embedding=1)
sage: K.<a> = NumberField(x^3-x+1/10, embedding=b^2)
sage: a+b
b^2 + b
sage: CC(a) == CC(b)^2
True
sage: K.coerce_embedding()
Generic morphism:
From: Number Field in a with defining polynomial x^3 - x + 1/10
To: Number Field in b with defining polynomial x^6 - x^2 + 1/10
Defn: a -> b^2
The QuadraticField and CyclotomicField constructors create an embedding by default unless otherwise specified.
sage: K.<zeta> = CyclotomicField(15)
sage: CC(zeta)
0.913545457642601 + 0.406736643075800*I
sage: L.<sqrtn3> = QuadraticField(-3)
sage: K(sqrtn3)
2*zeta^5 + 1
sage: sqrtn3 + zeta
2*zeta^5 + zeta + 1
An example involving a variable name that defines a function in PARI:
sage: theta = polygen(QQ, 'theta')
sage: M.<z> = NumberField([theta^3 + 4, theta^2 + 3]); M
Number Field in z0 with defining polynomial theta^3 + 4 over its base field
TESTS:
sage: x = QQ['x'].gen()
sage: y = ZZ['y'].gen()
sage: K = NumberField(x^3 + x + 3, 'a'); K
Number Field in a with defining polynomial x^3 + x + 3
sage: K.defining_polynomial().parent()
Univariate Polynomial Ring in x over Rational Field
sage: L = NumberField(y^3 + y + 3, 'a'); L
Number Field in a with defining polynomial y^3 + y + 3
sage: L.defining_polynomial().parent()
Univariate Polynomial Ring in y over Rational Field
sage: sage.rings.number_field.number_field._nf_cache = {}
sage: K.<x> = CyclotomicField(5)[]
sage: W.<a> = NumberField(x^2 + 1); W
Number Field in a with defining polynomial x^2 + 1 over its base field
sage: sage.rings.number_field.number_field._nf_cache = {}
sage: W1 = NumberField(x^2+1,'a')
sage: K.<x> = CyclotomicField(5)[]
sage: W.<a> = NumberField(x^2 + 1); W
Number Field in a with defining polynomial x^2 + 1 over its base field
Return the tower of number fields defined by the polynomials or number fields in the list v.
This is the field 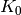 generated by a root of v[0] over its base field
generated by a root of v[0] over its base field
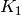 , which is in turn generated by a root of v[1] over its base field
, which is in turn generated by a root of v[1] over its base field
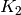 , etc, until
, etc, until 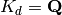 where
where  is the size of the list
is the size of the list  . If
all is False, then each v[i] must be irreducible over the previous
fields. Otherwise a list of all possible fields defined by all those
polynomials is output.
. If
all is False, then each v[i] must be irreducible over the previous
fields. Otherwise a list of all possible fields defined by all those
polynomials is output.
If names defines a variable name a, say, then the generators of the intermediate number fields are a0, a1, a2, ...
INPUT:
OUTPUT: a single number field or a list of number fields
EXAMPLES:
sage: k.<a,b,c> = NumberField([x^2 + 1, x^2 + 3, x^2 + 5]); k
Number Field in a with defining polynomial x^2 + 1 over its base field
sage: a^2
-1
sage: b^2
-3
sage: c^2
-5
sage: (a+b+c)^2
(2*b + 2*c)*a + 2*c*b - 9
The Galois group is a product of 3 groups of order 2:
sage: k.galois_group(type="pari")
Galois group PARI group [8, 1, 3, "E(8)=2[x]2[x]2"] of degree 8 of the Number Field in a with defining polynomial x^2 + 1 over its base field
Repeatedly calling base_field allows us to descend the internally constructed tower of fields:
sage: k.base_field()
Number Field in b with defining polynomial x^2 + 3 over its base field
sage: k.base_field().base_field()
Number Field in c with defining polynomial x^2 + 5
sage: k.base_field().base_field().base_field()
Rational Field
In the following example the second polynomial is reducible over the first, so we get an error:
sage: v = NumberField([x^3 - 2, x^3 - 2], names='a')
...
ValueError: defining polynomial (x^3 - 2) must be irreducible
We mix polynomial parent rings:
sage: k.<y> = QQ[]
sage: m = NumberField([y^3 - 3, x^2 + x + 1, y^3 + 2], 'beta')
sage: m
Number Field in beta0 with defining polynomial y^3 - 3 over its base field
sage: m.base_field ()
Number Field in beta1 with defining polynomial x^2 + x + 1 over its base field
A tower of quadratic fields:
sage: K.<a> = NumberField([x^2 + 3, x^2 + 2, x^2 + 1])
sage: K
Number Field in a0 with defining polynomial x^2 + 3 over its base field
sage: K.base_field()
Number Field in a1 with defining polynomial x^2 + 2 over its base field
sage: K.base_field().base_field()
Number Field in a2 with defining polynomial x^2 + 1
A bigger tower of quadratic fields.
sage: K.<a2,a3,a5,a7> = NumberField([x^2 + p for p in [2,3,5,7]]); K
Number Field in a2 with defining polynomial x^2 + 2 over its base field
sage: a2^2
-2
sage: a3^2
-3
sage: (a2+a3+a5+a7)^3
((6*a5 + 6*a7)*a3 + 6*a7*a5 - 47)*a2 + (6*a7*a5 - 45)*a3 - 41*a5 - 37*a7
Bases: sage.rings.number_field.number_field.NumberField_generic
Return an nxn matrix over RDF whose columns are the images of the
basis 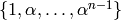 of self over
of self over
 (as vector spaces), where here
(as vector spaces), where here
 is the generator of self over
is the generator of self over
 , i.e. self.gen(0). If B is not None, return
the images of the vectors in B as the columns instead. If prec is
not None, use RealField(prec) instead of RDF.
, i.e. self.gen(0). If B is not None, return
the images of the vectors in B as the columns instead. If prec is
not None, use RealField(prec) instead of RDF.
This embedding is the so-called “Minkowski embedding” of a number
field in 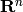 : given the
: given the  embeddings
embeddings
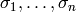 of self in
of self in
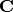 , write
, write 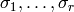 for the real embeddings, and
for the real embeddings, and
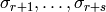 for choices of one of
each pair of complex conjugate embeddings (in our case, we simply
choose the one where the image of
for choices of one of
each pair of complex conjugate embeddings (in our case, we simply
choose the one where the image of  has positive
real part). Here
has positive
real part). Here 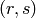 is the signature of self. Then the
Minkowski embedding is given by
is the signature of self. Then the
Minkowski embedding is given by
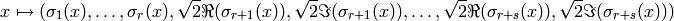
Equivalently, this is an embedding of self in 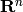 so
that the usual norm on
so
that the usual norm on 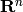 coincides with
coincides with
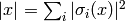 on self.
on self.
TODO: This could be much improved by implementing homomorphisms over VectorSpaces.
EXAMPLES:
sage: F.<alpha> = NumberField(x^3+2)
sage: F.Minkowski_embedding()
[ 1.00000000000000 -1.25992104989487 1.58740105196820]
[ 1.41421356237... 0.8908987181... -1.12246204830...]
[0.000000000000000 1.54308184421... 1.94416129723...]
sage: F.Minkowski_embedding([1, alpha+2, alpha^2-alpha])
[ 1.00000000000000 0.740078950105127 2.84732210186307]
[ 1.41421356237... 3.7193258428... -2.01336076644...]
[0.000000000000000 1.54308184421... 0.40107945302...]
sage: F.Minkowski_embedding() * (alpha + 2).vector().transpose()
[0.740078950105127]
[ 3.7193258428...]
[ 1.54308184421...]
A synonym for degree.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.absolute_degree()
2
A synonym for different.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.absolute_different()
Fractional ideal (2)
A synonym for discriminant.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.absolute_discriminant()
-4
An alias for gen(). This is provided for consistency with
relative fields, where the element returned by gen() only generates the
field over its base field (not necessarily over  ).
).
EXAMPLE:
sage: K.<a> = NumberField(x^2 - 17)
sage: K.absolute_generator()
a
A synonym for polynomial.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.absolute_polynomial()
x^2 + 1
A synonym for vector_space.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.absolute_vector_space()
(Vector space of dimension 2 over Rational Field,
Isomorphism map:
From: Vector space of dimension 2 over Rational Field
To: Number Field in i with defining polynomial x^2 + 1,
Isomorphism map:
From: Number Field in i with defining polynomial x^2 + 1
To: Vector space of dimension 2 over Rational Field)
Compute all Galois automorphisms of self.
This uses PARI’s nfgaloisconj and is much faster than root finding for many fields.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 10000)
sage: K.automorphisms()
[
Ring endomorphism of Number Field in a with defining polynomial x^2 + 10000
Defn: a |--> a,
Ring endomorphism of Number Field in a with defining polynomial x^2 + 10000
Defn: a |--> -a
]
Here’s a larger example, that would take some time if we found roots instead of using PARI’s specialized machinery:
sage: K = NumberField(x^6 - x^4 - 2*x^2 + 1, 'a')
sage: len(K.automorphisms())
2
 is the Galois closure of
is the Galois closure of  :
:
sage: L = NumberField(x^24 - 84*x^22 + 2814*x^20 - 15880*x^18 - 409563*x^16 - 8543892*x^14 + 25518202*x^12 + 32831026956*x^10 - 672691027218*x^8 - 4985379093428*x^6 + 320854419319140*x^4 + 817662865724712*x^2 + 513191437605441, 'a')
sage: len(L.automorphisms())
24
Returns the base field of self, which is always QQ
EXAMPLES:
sage: K = CyclotomicField(5)
sage: K.base_field()
Rational Field
Return number field isomorphic to self but with the given generator name.
INPUT:
Also, K.structure() returns from_K and to_K, where from_K is an isomorphism from K to self and to_K is an isomorphism from self to K.
EXAMPLES:
sage: K.<z> = NumberField(x^2 + 3); K
Number Field in z with defining polynomial x^2 + 3
sage: L.<ww> = K.change_names()
sage: L
Number Field in ww with defining polynomial x^2 + 3
sage: L.structure()[0]
Isomorphism given by variable name change map:
From: Number Field in ww with defining polynomial x^2 + 3
To: Number Field in z with defining polynomial x^2 + 3
sage: L.structure()[0](ww + 5/3)
z + 5/3
Compute all field embeddings of self into the field K (which need not even be a number field, e.g., it could be the complex numbers). This will return an identical result when given K as input again.
If possible, the most natural embedding of self into K is put first in the list.
INPUT:
EXAMPLES:
sage: K.<a> = NumberField(x^3 - 2)
sage: L.<a1> = K.galois_closure(); L
Number Field in a1 with defining polynomial x^6 + 40*x^3 + 1372
sage: K.embeddings(L)[0]
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Number Field in a1 with defining polynomial x^6 + 40*x^3 + 1372
Defn: a |--> 1/84*a1^4 + 13/42*a1
sage: K.embeddings(L) is K.embeddings(L)
True
We embed a quadratic field into a cyclotomic field:
sage: L.<a> = QuadraticField(-7)
sage: K = CyclotomicField(7)
sage: L.embeddings(K)
[
Ring morphism:
From: Number Field in a with defining polynomial x^2 + 7
To: Cyclotomic Field of order 7 and degree 6
Defn: a |--> 2*zeta7^4 + 2*zeta7^2 + 2*zeta7 + 1,
Ring morphism:
From: Number Field in a with defining polynomial x^2 + 7
To: Cyclotomic Field of order 7 and degree 6
Defn: a |--> -2*zeta7^4 - 2*zeta7^2 - 2*zeta7 - 1
]
We embed a cubic field in the complex numbers:
sage: K.<a> = NumberField(x^3 - 2)
sage: K.embeddings(CC)
[
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Complex Field with 53 bits of precision
Defn: a |--> -0.62996052494743... - 1.09112363597172*I,
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Complex Field with 53 bits of precision
Defn: a |--> -0.62996052494743... + 1.09112363597172*I,
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Complex Field with 53 bits of precision
Defn: a |--> 1.25992104989487
]
Return number field  that is the Galois closure of self,
i.e., is generated by all roots of the defining polynomial of
self, and possibly an embedding of self into
that is the Galois closure of self,
i.e., is generated by all roots of the defining polynomial of
self, and possibly an embedding of self into  .
.
INPUT:

EXAMPLES:
sage: K.<a> = NumberField(x^4 - 2)
sage: M = K.galois_closure('b'); M
Number Field in b with defining polynomial x^8 + 28*x^4 + 2500
sage: L.<a2> = K.galois_closure(); L
Number Field in a2 with defining polynomial x^8 + 28*x^4 + 2500
sage: K.galois_group(names=("a3")).order()
8
sage: phi = K.embeddings(L)[0]
sage: phi(K.0)
1/120*a2^5 + 19/60*a2
sage: phi(K.0).minpoly()
x^4 - 2
sage: L, phi = K.galois_closure('b', map=True)
sage: L
Number Field in b with defining polynomial x^8 + 28*x^4 + 2500
sage: phi
Ring morphism:
From: Number Field in a with defining polynomial x^4 - 2
To: Number Field in b with defining polynomial x^8 + 28*x^4 + 2500
Defn: a |--> 1/240*b^5 - 41/120*b
TESTS:
Let’s make sure we’re renaming correctly:
sage: L, phi = K.galois_closure('cc', map=True)
sage: L
Number Field in cc with defining polynomial x^8 + 28*x^4 + 2500
sage: phi
Ring morphism:
From: Number Field in a with defining polynomial x^4 - 2
To: Number Field in cc with defining polynomial x^8 + 28*x^4 + 2500
Defn: a |--> 1/240*cc^5 - 41/120*cc
Returns True since self is an absolute field.
EXAMPLES:
sage: K = CyclotomicField(5)
sage: K.is_absolute()
True
Return the maximal order, i.e., the ring of integers, associated to this number field.
INPUT:
EXAMPLES: In this example, the maximal order cannot be generated by a single element.
sage: k.<a> = NumberField(x^3 + x^2 - 2*x+8)
sage: o = k.maximal_order()
sage: o
Maximal Order in Number Field in a with defining polynomial x^3 + x^2 - 2*x + 8
We compute  -maximal orders for several
-maximal orders for several  . Note
that computing a
. Note
that computing a  -maximal order is much faster in
general than computing the maximal order:
-maximal order is much faster in
general than computing the maximal order:
sage: p = next_prime(10^22); q = next_prime(10^23)
sage: K.<a> = NumberField(x^3 - p*q)
sage: K.maximal_order([3]).basis()
[1/3*a^2 + 1/3*a + 1/3, a, a^2]
sage: K.maximal_order([2]).basis()
[1, a, a^2]
sage: K.maximal_order([p]).basis()
[1, a, a^2]
sage: K.maximal_order([q]).basis()
[1, a, a^2]
sage: K.maximal_order([p,3]).basis()
[1/3*a^2 + 1/3*a + 1/3, a, a^2]
An example with bigger discriminant:
sage: p = next_prime(10^97); q = next_prime(10^99)
sage: K.<a> = NumberField(x^3 - p*q)
sage: K.maximal_order(prime_range(10000)).basis()
[1, a, a^2]
Return a field isomorphic to self with a better defining polynomial if possible, along with field isomorphisms from the new field to self and from self to the new field.
EXAMPLES: We construct a compositum of 3 quadratic fields, then find an optimized representation and transform elements back and forth.
sage: K = NumberField([x^2 + p for p in [5, 3, 2]],'a').absolute_field('b'); K
Number Field in b with defining polynomial x^8 + 40*x^6 + 352*x^4 + 960*x^2 + 576
sage: L, from_L, to_L = K.optimized_representation()
sage: L # your answer may different, since algorithm is random
Number Field in a14 with defining polynomial x^8 + 4*x^6 + 7*x^4 + 36*x^2 + 81
sage: to_L(K.0) # random
4/189*a14^7 - 1/63*a14^6 + 1/27*a14^5 + 2/9*a14^4 - 5/27*a14^3 + 8/9*a14^2 + 3/7*a14 + 3/7
sage: from_L(L.0) # random
1/1152*a1^7 + 1/192*a1^6 + 23/576*a1^5 + 17/96*a1^4 + 37/72*a1^3 + 5/6*a1^2 + 55/24*a1 + 3/4
The transformation maps are mutually inverse isomorphisms.
sage: from_L(to_L(K.0))
b
sage: to_L(from_L(L.0)) # random
a14
Return optimized representations of many (but not necessarily all!) subfields of self of the given degree, or of all possible degrees if degree is 0.
EXAMPLES:
sage: K = NumberField([x^2 + p for p in [5, 3, 2]],'a').absolute_field('b'); K
Number Field in b with defining polynomial x^8 + 40*x^6 + 352*x^4 + 960*x^2 + 576
sage: L = K.optimized_subfields(name='b')
sage: L[0][0]
Number Field in b0 with defining polynomial x - 1
sage: L[1][0]
Number Field in b1 with defining polynomial x^2 - x + 1
sage: [z[0] for z in L] # random -- since algorithm is random
[Number Field in b0 with defining polynomial x - 1,
Number Field in b1 with defining polynomial x^2 - x + 1,
Number Field in b2 with defining polynomial x^4 - 5*x^2 + 25,
Number Field in b3 with defining polynomial x^4 - 2*x^2 + 4,
Number Field in b4 with defining polynomial x^8 + 4*x^6 + 7*x^4 + 36*x^2 + 81]
We examine one of the optimized subfields in more detail:
sage: M, from_M, to_M = L[2]
sage: M # random
Number Field in b2 with defining polynomial x^4 - 5*x^2 + 25
sage: from_M # may be slightly random
Ring morphism:
From: Number Field in b2 with defining polynomial x^4 - 5*x^2 + 25
To: Number Field in a1 with defining polynomial x^8 + 40*x^6 + 352*x^4 + 960*x^2 + 576
Defn: b2 |--> -5/1152*a1^7 + 1/96*a1^6 - 97/576*a1^5 + 17/48*a1^4 - 95/72*a1^3 + 17/12*a1^2 - 53/24*a1 - 1
The to_M map is None, since there is no map from K to M:
sage: to_M
We apply the from_M map to the generator of M, which gives a
rather large element of  :
:
sage: from_M(M.0) # random
-5/1152*a1^7 + 1/96*a1^6 - 97/576*a1^5 + 17/48*a1^4 - 95/72*a1^3 + 17/12*a1^2 - 53/24*a1 - 1
Nevertheless, that large-ish element lies in a degree 4 subfield:
sage: from_M(M.0).minpoly() # random
x^4 - 5*x^2 + 25
Return the order with given ring generators in the maximal order of this number field.
INPUT:
EXAMPLES:
sage: k.<i> = NumberField(x^2 + 1)
sage: k.order(2*i)
Order in Number Field in i with defining polynomial x^2 + 1
sage: k.order(10*i)
Order in Number Field in i with defining polynomial x^2 + 1
sage: k.order(3)
...
ValueError: the rank of the span of gens is wrong
sage: k.order(i/2)
...
ValueError: each generator must be integral
Alternatively, an order can be constructed by adjoining elements to
 :
:
sage: K.<a> = NumberField(x^3 - 2) sage: ZZ[a] Order in Number Field in a0 with defining polynomial x^3 - 2
TESTS:
We verify that trac #2480 is fixed:
sage: K.<a> = NumberField(x^4 + 4*x^2 + 2)
sage: B = K.integral_basis()
sage: K.order(*B)
Order in Number Field in a with defining polynomial x^4 + 4*x^2 + 2
sage: K.order(B)
Order in Number Field in a with defining polynomial x^4 + 4*x^2 + 2
sage: K.order(gens=B)
Order in Number Field in a with defining polynomial x^4 + 4*x^2 + 2
Return the collection of all infinite places of self.
By default, this returns the set of real places as homomorphisms into RIF first, followed by a choice of one of each pair of complex conjugate homomorphisms into CIF.
On the other hand, if prec is not None, we simply return places
into RealField(prec) and ComplexField(prec) (or RDF, CDF if
prec=53). One can also use prec=infinity, which returns embeddings
into the field 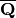 of algebraic numbers (or its subfield
of algebraic numbers (or its subfield
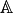 of algebraic reals); this permits exact computatation, but
can be extremely slow.
of algebraic reals); this permits exact computatation, but
can be extremely slow.
There is an optional flag all_complex, which defaults to False. If all_complex is True, then the real embeddings are returned as embeddings into CIF instead of RIF.
EXAMPLES:
sage: F.<alpha> = NumberField(x^3-100*x+1) ; F.places()
[Ring morphism:
From: Number Field in alpha with defining polynomial x^3 - 100*x + 1
To: Real Field with 106 bits of precision
Defn: alpha |--> -10.00499625499181184573367219280,
Ring morphism:
From: Number Field in alpha with defining polynomial x^3 - 100*x + 1
To: Real Field with 106 bits of precision
Defn: alpha |--> 0.01000001000003000012000055000273,
Ring morphism:
From: Number Field in alpha with defining polynomial x^3 - 100*x + 1
To: Real Field with 106 bits of precision
Defn: alpha |--> 9.994996244991781845613530439509]
sage: F.<alpha> = NumberField(x^3+7) ; F.places()
[Ring morphism:
From: Number Field in alpha with defining polynomial x^3 + 7
To: Real Field with 106 bits of precision
Defn: alpha |--> -1.912931182772389101199116839549,
Ring morphism:
From: Number Field in alpha with defining polynomial x^3 + 7
To: Complex Field with 53 bits of precision
Defn: alpha |--> 0.956465591386195 + 1.65664699997230*I]
sage: F.<alpha> = NumberField(x^3+7) ; F.places(all_complex=True)
[Ring morphism:
From: Number Field in alpha with defining polynomial x^3 + 7
To: Complex Field with 53 bits of precision
Defn: alpha |--> -1.91293118277239,
Ring morphism:
From: Number Field in alpha with defining polynomial x^3 + 7
To: Complex Field with 53 bits of precision
Defn: alpha |--> 0.956465591386195 + 1.65664699997230*I]
sage: F.places(prec=10)
[Ring morphism:
From: Number Field in alpha with defining polynomial x^3 + 7
To: Real Field with 10 bits of precision
Defn: alpha |--> -1.9,
Ring morphism:
From: Number Field in alpha with defining polynomial x^3 + 7
To: Complex Field with 10 bits of precision
Defn: alpha |--> 0.96 + 1.7*I]
Return all real places of self as homomorphisms into RIF.
EXAMPLES:
sage: F.<alpha> = NumberField(x^4-7) ; F.real_places()
[Ring morphism:
From: Number Field in alpha with defining polynomial x^4 - 7
To: Real Field with 106 bits of precision
Defn: alpha |--> -1.626576561697785743211232345494,
Ring morphism:
From: Number Field in alpha with defining polynomial x^4 - 7
To: Real Field with 106 bits of precision
Defn: alpha |--> 1.626576561697785743211232345494]
A synonym for degree.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.relative_degree()
2
A synonym for different.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.relative_different()
Fractional ideal (2)
A synonym for discriminant.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.relative_discriminant()
-4
A synonym for polynomial.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.relative_polynomial()
x^2 + 1
A synonym for vector_space.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.relative_vector_space()
(Vector space of dimension 2 over Rational Field,
Isomorphism map:
From: Vector space of dimension 2 over Rational Field
To: Number Field in i with defining polynomial x^2 + 1,
Isomorphism map:
From: Number Field in i with defining polynomial x^2 + 1
To: Vector space of dimension 2 over Rational Field)
Given an element in self or an embedding of a subfield into self,
return a relative number field  isomorphic to self that is relative
over the absolute field
isomorphic to self that is relative
over the absolute field 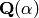 or the domain of
or the domain of 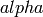 , along
with isomorphisms from
, along
with isomorphisms from  to self and from self to
to self and from self to  .
.
INPUT:
OUTPUT:
K – relative number field
Also, K.structure() returns from_K and to_K, where from_K is an isomorphism from K to self and to_K is an isomorphism from self to K.
EXAMPLES:
sage: K.<a> = NumberField(x^10 - 2)
sage: L.<c,d> = K.relativize(a^4 + a^2 + 2); L
Number Field in c with defining polynomial x^2 - 1/5*d^4 + 8/5*d^3 - 23/5*d^2 + 7*d - 18/5 over its base field
sage: c.absolute_minpoly()
x^10 - 2
sage: d.absolute_minpoly()
x^5 - 10*x^4 + 40*x^3 - 90*x^2 + 110*x - 58
sage: (a^4 + a^2 + 2).minpoly()
x^5 - 10*x^4 + 40*x^3 - 90*x^2 + 110*x - 58
sage: from_L, to_L = L.structure()
sage: to_L(a)
c
sage: to_L(a^4 + a^2 + 2)
d
sage: from_L(to_L(a^4 + a^2 + 2))
a^4 + a^2 + 2
The following demonstrates distinct embeddings of a subfield into a larger field:
sage: K.<a> = NumberField(x^4 + 2*x^2 + 2)
sage: K0 = K.subfields(2)[0][0]; K0
Number Field in a0 with defining polynomial x^2 - 2*x + 2
sage: rho, tau = K0.embeddings(K)
sage: L0 = K.relativize(rho(K0.gen()), 'b'); L0
Number Field in b0 with defining polynomial x^2 - b1 + 2 over its base field
sage: L1 = K.relativize(rho, 'b'); L1
Number Field in b0 with defining polynomial x^2 - a0 + 2 over its base field
sage: L2 = K.relativize(tau, 'b'); L2
Number Field in b0 with defining polynomial x^2 + a0 over its base field
sage: L0.base_field() is K0
False
sage: L1.base_field() is K0
True
sage: L2.base_field() is K0
True
Here we see that with the different embeddings, the relative norms are different:
sage: a0 = K0.gen()
sage: L1_into_K, K_into_L1 = L1.structure()
sage: L2_into_K, K_into_L2 = L2.structure()
sage: len(K.factor(41))
4
sage: w1 = -a^2 + a + 1; P = K.ideal([w1])
sage: Pp = L1.ideal(K_into_L1(w1)).ideal_below(); Pp == K0.ideal([4*a0 + 1])
True
sage: Pp == w1.norm(rho)
True
sage: w2 = a^2 + a - 1; Q = K.ideal([w2])
sage: Qq = L2.ideal(K_into_L2(w2)).ideal_below(); Qq == K0.ideal([-4*a0 + 9])
True
sage: Qq == w2.norm(tau)
True
sage: Pp == Qq
False
TESTS:
We can relativize over the whole field:
sage: K.<a> = NumberField(x^4 + 2*x^2 + 2)
sage: K.relativize(K.gen(), 'a')
Number Field in a0 with defining polynomial x - a1 over its base field
sage: K.relativize(2*K.gen(), 'a')
Number Field in a0 with defining polynomial x - 1/2*a1 over its base field
We can relativize over the prime field:
sage: L = K.relativize(K(1), 'a'); L
Number Field in a0 with defining polynomial x^4 + 2*x^2 + 2 over its base field
sage: L.base_field()
Number Field in a1 with defining polynomial x - 1
sage: L.base_field().base_field()
Rational Field
sage: L = K.relativize(K(2), 'a'); L
Number Field in a0 with defining polynomial x^4 + 2*x^2 + 2 over its base field
sage: L.base_field()
Number Field in a1 with defining polynomial x - 2
sage: L.base_field().base_field()
Rational Field
We can relativize over a relative field:
sage: K.<z> = CyclotomicField(16)
sage: L, L_into_K, _ = K.subfields(4)[0]; L
Number Field in z0 with defining polynomial x^4 + 16
sage: F, F_into_L, _ = L.subfields(2)[0]; F
Number Field in z00 with defining polynomial x^2 + 64
sage: L_over_F = L.relativize(F_into_L, 'c'); L_over_F
Number Field in c0 with defining polynomial x^2 - 1/2*z00 over its base field
sage: L_over_F_into_L, _ = L_over_F.structure()
sage: K_over_rel = K.relativize(L_into_K * L_over_F_into_L, 'a'); K_over_rel
Number Field in a0 with defining polynomial x^2 - 1/2*c0 over its base field
sage: K_over_rel.base_field() is L_over_F
True
sage: K_over_rel.structure()
(Relative number field morphism:
From: Number Field in a0 with defining polynomial x^2 - 1/2*c0 over its base field
To: Cyclotomic Field of order 16 and degree 8
Defn: a0 |--> z
c0 |--> 2*z^2
z00 |--> 8*z^4, Ring morphism:
From: Cyclotomic Field of order 16 and degree 8
To: Number Field in a0 with defining polynomial x^2 - 1/2*c0 over its base field
Defn: z |--> a0)
We can relativize over a really large field. This requires great care to not factor or do any operation that would trigger a pari nfinit() internally:
sage: K.<a> = CyclotomicField(3^3*2^3)
sage: R = K.relativize(a^(3^2), 't'); R
Number Field in t0 with defining polynomial x^9 - t1 over its base field
sage: R.structure()
(Relative number field morphism:
From: Number Field in t0 with defining polynomial x^9 - t1 over its base field
To: Cyclotomic Field of order 216 and degree 72
Defn: t0 |--> a
t1 |--> a^9,
Ring morphism:
From: Cyclotomic Field of order 216 and degree 72
To: Number Field in t0 with defining polynomial x^9 - t1 over its base field
Defn: a |--> t0)
Return all subfields of self of the given degree, or of all possible degrees if degree is 0. The subfields are returned as absolute fields together with an embedding into self. For the case of the field itself, the reverse isomorphism is also provided.
EXAMPLES:
sage: K.<a> = NumberField( [x^3 - 2, x^2 + x + 1] )
sage: K = K.absolute_field('b')
sage: S = K.subfields()
sage: len(S)
6
sage: [k[0].polynomial() for k in S]
[x - 3,
x^2 - 3*x + 9,
x^3 - 3*x^2 + 3*x + 1,
x^3 - 3*x^2 + 3*x + 1,
x^3 - 3*x^2 + 3*x - 17,
x^6 - 3*x^5 + 6*x^4 - 11*x^3 + 12*x^2 + 3*x + 1]
sage: R.<t> = QQ[]
sage: L = NumberField(t^3 - 3*t + 1, 'c')
sage: [k[1] for k in L.subfields()]
[Ring morphism:
From: Number Field in c0 with defining polynomial t
To: Number Field in c with defining polynomial t^3 - 3*t + 1
Defn: 0 |--> 0,
Ring morphism:
From: Number Field in c1 with defining polynomial t^3 - 3*t + 1
To: Number Field in c with defining polynomial t^3 - 3*t + 1
Defn: c1 |--> c]
sage: L.subfields(2)
[]
Return a vector space V and isomorphisms self –> V and V –> self.
OUTPUT:
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 2)
sage: V, from_V, to_V = k.vector_space()
sage: from_V(V([1,2,3]))
3*a^2 + 2*a + 1
sage: to_V(1 + 2*a + 3*a^2)
(1, 2, 3)
sage: V
Vector space of dimension 3 over Rational Field
sage: to_V
Isomorphism map:
From: Number Field in a with defining polynomial x^3 + 2
To: Vector space of dimension 3 over Rational Field
sage: from_V(to_V(2/3*a - 5/8))
2/3*a - 5/8
sage: to_V(from_V(V([0,-1/7,0])))
(0, -1/7, 0)
This is used in pickling generic number fields.
EXAMPLES:
sage: from sage.rings.number_field.number_field import NumberField_generic_v1
sage: R.<x> = QQ[]
sage: NumberField_generic_v1(x^2 + 1, 'i', 'i')
Number Field in i with defining polynomial x^2 + 1
Bases: sage.rings.number_field.number_field.NumberField_absolute
Create a cyclotomic extension of the rational field.
The command CyclotomicField(n) creates the n-th cyclotomic field, obtained by adjoining an n-th root of unity to the rational field.
EXAMPLES:
sage: CyclotomicField(3)
Cyclotomic Field of order 3 and degree 2
sage: CyclotomicField(18)
Cyclotomic Field of order 18 and degree 6
sage: z = CyclotomicField(6).gen(); z
zeta6
sage: z^3
-1
sage: (1+z)^3
6*zeta6 - 3
sage: K = CyclotomicField(197)
sage: loads(K.dumps()) == K
True
sage: loads((z^2).dumps()) == z^2
True
sage: cf12 = CyclotomicField( 12 )
sage: z12 = cf12.0
sage: cf6 = CyclotomicField( 6 )
sage: z6 = cf6.0
sage: FF = Frac( cf12['x'] )
sage: x = FF.0
sage: z6*x^3/(z6 + x)
zeta12^2*x^3/(x + zeta12^2)
sage: cf6 = CyclotomicField(6) ; z6 = cf6.gen(0)
sage: cf3 = CyclotomicField(3) ; z3 = cf3.gen(0)
sage: cf3(z6)
zeta3 + 1
sage: cf6(z3)
zeta6 - 1
sage: type(cf6(z3))
<type 'sage.rings.number_field.number_field_element_quadratic.NumberFieldElement_quadratic'>
sage: cf1 = CyclotomicField(1) ; z1 = cf1.0
sage: cf3(z1)
1
sage: type(cf3(z1))
<type 'sage.rings.number_field.number_field_element_quadratic.NumberFieldElement_quadratic'>
Return the embedding of this cyclotomic field into the approximate
complex field with precision prec obtained by sending the generator
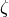 of self to exp(2*pi*i/n), where
of self to exp(2*pi*i/n), where  is
the multiplicative order of
is
the multiplicative order of 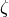 .
.
EXAMPLES:
sage: C = CyclotomicField(4)
sage: C.complex_embedding()
Ring morphism:
From: Cyclotomic Field of order 4 and degree 2
To: Complex Field with 53 bits of precision
Defn: zeta4 |--> 6.12323399573677e-17 + 1.00000000000000*I
Note in the example above that the way zeta is computed (using sin and cosine in MPFR) means that only the prec bits of the number after the decimal point are valid.
sage: K = CyclotomicField(3)
sage: phi = K.complex_embedding(10)
sage: phi(K.0)
-0.50 + 0.87*I
sage: phi(K.0^3)
1.0
sage: phi(K.0^3 - 1)
0
sage: phi(K.0^3 + 7)
8.0
Return all embeddings of this cyclotomic field into the approximate complex field with precision prec.
If you want 53-bit double precision, which is faster but less reliable, then do self.embeddings(CDF).
EXAMPLES:
sage: CyclotomicField(5).complex_embeddings()
[
Ring morphism:
From: Cyclotomic Field of order 5 and degree 4
To: Complex Field with 53 bits of precision
Defn: zeta5 |--> 0.309016994374947 + 0.951056516295154*I,
Ring morphism:
From: Cyclotomic Field of order 5 and degree 4
To: Complex Field with 53 bits of precision
Defn: zeta5 |--> -0.809016994374947 + 0.587785252292473*I,
Ring morphism:
From: Cyclotomic Field of order 5 and degree 4
To: Complex Field with 53 bits of precision
Defn: zeta5 |--> -0.809016994374947 - 0.587785252292473*I,
Ring morphism:
From: Cyclotomic Field of order 5 and degree 4
To: Complex Field with 53 bits of precision
Defn: zeta5 |--> 0.309016994374947 - 0.951056516295154*I
]
Returns the different ideal of the cyclotomic field self.
EXAMPLES:
sage: C20 = CyclotomicField(20)
sage: C20.different()
Fractional ideal (-4*zeta20^7 + 8*zeta20^5 - 12*zeta20^3 + 6*zeta20)
sage: C18 = CyclotomicField(18)
sage: D = C18.different().norm()
sage: D == C18.discriminant().abs()
True
Returns the discriminant of the ring of integers of the cyclotomic field self, or if v is specified, the determinant of the trace pairing on the elements of the list v.
Uses the formula for the discriminant of a prime power cyclotomic field and Hilbert Theorem 88 on the discriminant of composita.
INPUT:
OUTPUT: Integer if v is omitted, and Rational otherwise.
EXAMPLES:
sage: CyclotomicField(20).discriminant()
4000000
sage: CyclotomicField(18).discriminant()
-19683
Return a list of elements of this number field that are a basis for the full ring of integers.
This field is cyclomotic, so this is a trivial computation, since the power basis on the generator is an integral basis. Thus the v parameter is ignored.
EXAMPLES:
sage: CyclotomicField(5).integral_basis()
[1, zeta5, zeta5^2, zeta5^3]
Return True since all cyclotomic fields are automatically Galois.
EXAMPLES:
sage: CyclotomicField(29).is_galois()
True
Return True if the cyclotomic field self is isomorphic as a number field to other.
EXAMPLES:
sage: CyclotomicField(11).is_isomorphic(CyclotomicField(22))
True
sage: CyclotomicField(11).is_isomorphic(CyclotomicField(23))
False
sage: CyclotomicField(3).is_isomorphic(NumberField(x^2 + x +1, 'a'))
True
Return the next prime integer  that splits completely in
this cyclotomic field (and does not ramify).
that splits completely in
this cyclotomic field (and does not ramify).
EXAMPLES:
sage: K.<z> = CyclotomicField(3)
sage: K.next_split_prime(7)
13
Return number of roots of unity in this cyclotomic field.
EXAMPLES:
sage: K.<a> = CyclotomicField(21)
sage: K.number_of_roots_of_unity()
42
Return a generator of the roots of unity in this field.
EXAMPLES:
sage: K.<a> = CyclotomicField(3)
sage: z = K.primitive_root_of_unity(); z
-a
sage: z.multiplicative_order()
6
sage: K.<a> = CyclotomicField(10)
sage: z = K.primitive_root_of_unity(); z
a
sage: z.multiplicative_order()
10
Return all embeddings of this cyclotomic field into the approximate real field with precision prec.
Mostly, of course, there are no such embeddings.
EXAMPLES:
sage: CyclotomicField(4).real_embeddings()
[]
sage: CyclotomicField(2).real_embeddings()
[
Ring morphism:
From: Cyclotomic Field of order 2 and degree 1
To: Real Field with 53 bits of precision
Defn: -1 |--> -1.00000000000000
]
Return all the roots of unity in this cyclotomic field, primitive or not.
EXAMPLES:
sage: K.<a> = CyclotomicField(3)
sage: zs = K.roots_of_unity(); zs
[1, a, -a - 1, -1, -a, a + 1]
sage: [ z**K.number_of_roots_of_unity() for z in zs ]
[1, 1, 1, 1, 1, 1]
Return (r1, r2), where r1 and r2 are the number of real embeddings and pairs of complex embeddings of this cyclotomic field, respectively.
Trivial since, apart from QQ, cyclotomic fields are totally complex.
EXAMPLES:
sage: CyclotomicField(5).signature()
(0, 2)
sage: CyclotomicField(2).signature()
(1, 0)
Returns an element of multiplicative order  in this this
cyclotomic field, if there is one. Raises a ValueError if there is
not.
in this this
cyclotomic field, if there is one. Raises a ValueError if there is
not.
INPUT:
OUTPUT: root of unity or list
EXAMPLES:
sage: k = CyclotomicField(7)
sage: k.zeta()
zeta7
sage: k.zeta().multiplicative_order()
7
sage: k = CyclotomicField(49)
sage: k.zeta().multiplicative_order()
49
sage: k.zeta(7).multiplicative_order()
7
sage: k.zeta()
zeta49
sage: k.zeta(7)
zeta49^7
sage: K.<a> = CyclotomicField(7)
sage: K.zeta(14, all=True)
[-a^4, -a^5, a^5 + a^4 + a^3 + a^2 + a + 1, -a, -a^2, -a^3]
sage: K.<a> = CyclotomicField(10)
sage: K.zeta(20, all=True)
...
ValueError: n (=20) does not divide order of generator
sage: K.<a> = CyclotomicField(5)
sage: K.zeta(4)
...
ValueError: n (=4) does not divide order of generator
sage: v = K.zeta(5, all=True); v
[a, a^2, a^3, -a^3 - a^2 - a - 1]
sage: [b^5 for b in v]
[1, 1, 1, 1]
Return the order of the maximal root of unity contained in this cyclotomic field.
EXAMPLES:
sage: CyclotomicField(1).zeta_order()
2
sage: CyclotomicField(4).zeta_order()
4
sage: CyclotomicField(5).zeta_order()
10
sage: CyclotomicField(5)._n()
5
sage: CyclotomicField(389).zeta_order()
778
This is used in pickling cyclotomic fields.
EXAMPLES:
sage: from sage.rings.number_field.number_field import NumberField_cyclotomic_v1
sage: NumberField_cyclotomic_v1(5,'a')
Cyclotomic Field of order 5 and degree 4
sage: NumberField_cyclotomic_v1(5,'a').variable_name()
'a'
Bases: sage.rings.number_field.number_field_base.NumberField
EXAMPLES:
sage: K.<a> = NumberField(x^3 - 2); K
Number Field in a with defining polynomial x^3 - 2
sage: loads(K.dumps()) == K
True
Returns a list of representatives which generate the S-class group of this number field over its base field.
INPUT:
OUTPUT:
A list of fractional ideal representatives of the class group generators.
EXAMPLE:
A well known example:
sage: K.<a> = QuadraticField(-5)
sage: K.S_class_group([])
[Fractional ideal (2, a + 1)]
When we include the prime 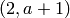 , the S-class group becomes
trivial:
, the S-class group becomes
trivial:
sage: K.S_class_group([K.ideal(2,a+1)])
[]
Returns a list of generators of the S-units.
INPUT:
- ``S`` - a set of primes of the base field
OUTPUT:
A list of generators of the unit group.
EXAMPLE:
sage: K.<a> = QuadraticField(-3)
sage: K.unit_group()
Unit group with structure C6 of Number Field in a with defining polynomial x^2 + 3
sage: K.S_units([])
[-1/2*a + 1/2]
sage: K.S_units([])[0].multiplicative_order()
6
An example in a relative extension (see trac #8722):
sage: L.<a,b> = NumberField([x^2 + 1, x^2 - 5])
sage: p = L.ideal((-1/2*b - 1/2)*a + 1/2*b - 1/2)
sage: W = L.S_units([p]); [x.norm() for x in W]
[9, 1, 1]
Return the degree of self over  .
.
EXAMPLES:
sage: NumberField(x^3 + x^2 + 997*x + 1, 'a').absolute_degree()
3
sage: NumberField(x + 1, 'a').absolute_degree()
1
sage: NumberField(x^997 + 17*x + 3, 'a', check=False).absolute_degree()
997
Returns self as an absolute extension over QQ.
OUTPUT:
Also, K.structure() returns from_K and to_K, where from_K is an isomorphism from K to self and to_K is an isomorphism from self to K.
EXAMPLES:
sage: K = CyclotomicField(5)
sage: K.absolute_field('a')
Number Field in a with defining polynomial x^4 + x^3 + x^2 + x + 1
Return the algebraic closure of self (which is QQbar).
EXAMPLES:
sage: K.<i> = QuadraticField(-1)
sage: K.algebraic_closure()
Algebraic Field
sage: K.<a> = NumberField(x^3-2)
sage: K.algebraic_closure()
Algebraic Field
sage: K = CyclotomicField(23)
sage: K.algebraic_closure()
Algebraic Field
Given the number field self, construct another isomorphic number
field  generated by the element alpha of self, along
with isomorphisms from
generated by the element alpha of self, along
with isomorphisms from  to self and from self to
to self and from self to
 .
.
EXAMPLES:
sage: L.<i> = NumberField(x^2 + 1); L
Number Field in i with defining polynomial x^2 + 1
sage: K, from_K, to_K = L.change_generator(i/2 + 3)
sage: K
Number Field in i0 with defining polynomial x^2 - 6*x + 37/4
sage: from_K
Ring morphism:
From: Number Field in i0 with defining polynomial x^2 - 6*x + 37/4
To: Number Field in i with defining polynomial x^2 + 1
Defn: i0 |--> 1/2*i + 3
sage: to_K
Ring morphism:
From: Number Field in i with defining polynomial x^2 + 1
To: Number Field in i0 with defining polynomial x^2 - 6*x + 37/4
Defn: i |--> 2*i0 - 6
We can also do
sage: K.<c>, from_K, to_K = L.change_generator(i/2 + 3); K
Number Field in c with defining polynomial x^2 - 6*x + 37/4
We compute the image of the generator 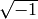 of
of  .
.
sage: to_K(i)
2*c - 6
Note that the image is indeed a square root of -1.
sage: to_K(i)^2
-1
sage: from_K(to_K(i))
i
sage: to_K(from_K(c))
c
Return the characteristic of this number field, which is of course 0.
EXAMPLES:
sage: k.<a> = NumberField(x^99 + 2); k
Number Field in a with defining polynomial x^99 + 2
sage: k.characteristic()
0
Return the class group of the ring of integers of this number field.
INPUT:
OUTPUT: The class group of this number field.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 23)
sage: G = K.class_group(); G
Class group of order 3 with structure C3 of Number Field in a with defining polynomial x^2 + 23
sage: G.0
Fractional ideal class (2, 1/2*a - 1/2)
sage: G.gens()
[Fractional ideal class (2, 1/2*a - 1/2)]
sage: G.number_field()
Number Field in a with defining polynomial x^2 + 23
sage: G is K.class_group()
True
sage: G is K.class_group(proof=False)
False
sage: G.gens()
[Fractional ideal class (2, 1/2*a - 1/2)]
There can be multiple generators:
sage: k.<a> = NumberField(x^2 + 20072)
sage: G = k.class_group(); G
Class group of order 76 with structure C38 x C2 of Number Field in a with defining polynomial x^2 + 20072
sage: G.0 # random
Fractional ideal class (41, a + 10)
sage: G.0^38
Trivial principal fractional ideal class
sage: G.1 # random
Fractional ideal class (2, -1/2*a)
sage: G.1^2
Trivial principal fractional ideal class
Class groups of Hecke polynomials tend to be very small:
sage: f = ModularForms(97, 2).T(2).charpoly()
sage: f.factor()
(x - 3) * (x^3 + 4*x^2 + 3*x - 1) * (x^4 - 3*x^3 - x^2 + 6*x - 1)
sage: [NumberField(g,'a').class_group().order() for g,_ in f.factor()]
[1, 1, 1]
Return the class number of this number field, as an integer.
INPUT:
EXAMPLES:
sage: NumberField(x^2 + 23, 'a').class_number()
3
sage: NumberField(x^2 + 163, 'a').class_number()
1
sage: NumberField(x^3 + x^2 + 997*x + 1, 'a').class_number(proof=False)
1539
Returns the completion of self at  to the specified
precision. Only implemented at archimedean places, and then only if
an embedding has been fixed.
to the specified
precision. Only implemented at archimedean places, and then only if
an embedding has been fixed.
EXAMPLES:
sage: K.<a> = QuadraticField(2)
sage: K.completion(infinity, 100)
Real Field with 100 bits of precision
sage: K.<zeta> = CyclotomicField(12)
sage: K.completion(infinity, 53, extras={'type': 'RDF'})
Complex Double Field
sage: zeta + 1.5 # implicit test
2.36602540378444 + 0.500000000000000*I
Return all homomorphisms of this number field into the approximate complex field with precision prec.
This always embeds into an MPFR based complex field. If you want embeddings into the 53-bit double precision, which is faster, use self.embeddings(CDF).
EXAMPLES:
sage: k.<a> = NumberField(x^5 + x + 17)
sage: v = k.complex_embeddings()
sage: ls = [phi(k.0^2) for phi in v] ; ls # random order
[2.97572074038...,
-2.40889943716 + 1.90254105304*I,
-2.40889943716 - 1.90254105304*I,
0.921039066973 + 3.07553311885*I,
0.921039066973 - 3.07553311885*I]
sage: K.<a> = NumberField(x^3 + 2)
sage: ls = K.complex_embeddings() ; ls # random order
[
Ring morphism:
From: Number Field in a with defining polynomial x^3 + 2
To: Complex Double Field
Defn: a |--> -1.25992104989...,
Ring morphism:
From: Number Field in a with defining polynomial x^3 + 2
To: Complex Double Field
Defn: a |--> 0.629960524947 - 1.09112363597*I,
Ring morphism:
From: Number Field in a with defining polynomial x^3 + 2
To: Complex Double Field
Defn: a |--> 0.629960524947 + 1.09112363597*I
]
List of all possible composite number fields formed from self and other, together with (optionally) embeddings into the compositum; see the documentation for both_maps below.
If preserve_embedding is True and if self and other both have embeddings into the same ambient field, or into fields which are contained in a common field, only the compositum respecting both embeddings is returned. If one (or both) of self or other does not have an embedding or preserve_embedding is False, all possible composite number fields are returned.
INPUT:
OUTPUT:
EXAMPLES:
sage: K.<a> = NumberField(x^4 - 2)
sage: K.composite_fields(K)
[Number Field in a with defining polynomial x^4 - 2,
Number Field in a0 with defining polynomial x^8 + 28*x^4 + 2500]
A particular compositum is selected, together with compatible maps into the compositum, if the fields are endowed with a real or complex embedding:
sage: K1 = NumberField(x^4 - 2, 'a', embedding=RR(2^(1/4)))
sage: K2 = NumberField(x^4 - 2, 'a', embedding=RR(-2^(1/4)))
sage: K1.composite_fields(K2)
[Number Field in a with defining polynomial x^4 - 2]
sage: [F, f, g, k], = K1.composite_fields(K2, both_maps=True); F
Number Field in a with defining polynomial x^4 - 2
sage: f(K1.0), g(K2.0)
(a, -a)
With preserve_embedding set to False, the embeddings are ignored:
sage: K1.composite_fields(K2, preserve_embedding=False)
[Number Field in a with defining polynomial x^4 - 2,
Number Field in a0 with defining polynomial x^8 + 28*x^4 + 2500]
Changing the embedding selects a different compositum:
sage: K3 = NumberField(x^4 - 2, 'a', embedding=CC(2^(1/4)*I))
sage: [F, f, g, k], = K1.composite_fields(K3, both_maps=True); F
Number Field in a0 with defining polynomial x^8 + 28*x^4 + 2500
sage: f(K1.0), g(K3.0)
(1/240*a0^5 - 41/120*a0, 1/120*a0^5 + 19/60*a0)
If no embeddings are specified, the maps into the composite are chosen arbitrarily:
sage: Q1.<a> = NumberField(x^4 + 10*x^2 + 1)
sage: Q2.<b> = NumberField(x^4 + 16*x^2 + 4)
sage: Q1.composite_fields(Q2, 'c')
[Number Field in c with defining polynomial x^8 + 64*x^6 + 904*x^4 + 3840*x^2 + 3600]
sage: F, Q1_into_F, Q2_into_F, k = Q1.composite_fields(Q2, 'c', both_maps=True)[0]
sage: Q1_into_F
Ring morphism:
From: Number Field in a with defining polynomial x^4 + 10*x^2 + 1
To: Number Field in c with defining polynomial x^8 + 64*x^6 + 904*x^4 + 3840*x^2 + 3600
Defn: a |--> 19/14400*c^7 + 137/1800*c^5 + 2599/3600*c^3 + 8/15*c
TESTS:
Let’s check that embeddings are being respected:
sage: x = ZZ['x'].0
sage: K0.<b> = CyclotomicField(7, 'a').subfields(3)[0][0].change_names()
sage: K1.<a1> = K0.extension(x^2 - 2*b^2, 'a1').absolute_field()
sage: K2.<a2> = K0.extension(x^2 - 3*b^2, 'a2').absolute_field()
We need embeddings, so we redefine:
sage: L1.<a1> = NumberField(K1.polynomial(), 'a1', embedding=CC.0)
sage: L2.<a2> = NumberField(K2.polynomial(), 'a2', embedding=CC.0)
sage: [CDF(a1), CDF(a2)]
[-0.629384245426, -0.77083512672]
and we get the same embeddings via the compositum:
sage: F, L1_into_F, L2_into_F, k = L1.composite_fields(L2, both_maps=True)[0]
sage: [CDF(L1_into_F(L1.gen())), CDF(L2_into_F(L2.gen()))]
[-0.629384245426, -0.77083512672]
Let’s check that if only one field has an embedding, the resulting fields do not have embeddings:
sage: L1.composite_fields(K2)[0].coerce_embedding() is None
True
sage: L2.composite_fields(K1)[0].coerce_embedding() is None
True
We check that other can be a relative number field:
sage: L.<a, b> = NumberField([x^3 - 5, x^2 + 3])
sage: CyclotomicField(3, 'w').composite_fields(L, both_maps=True)
[(Number Field in a with defining polynomial x^3 - 5 over its base field, Ring morphism:
From: Cyclotomic Field of order 3 and degree 2
To: Number Field in a with defining polynomial x^3 - 5 over its base field
Defn: w |--> -1/2*b - 1/2, Relative number field endomorphism of Number Field in a with defining polynomial x^3 - 5 over its base field
Defn: a |--> a
b |--> b, None)]
Return the defining polynomial of this number field.
This is exactly the same as self.polynomal().
EXAMPLES:
sage: k5.<z> = CyclotomicField(5)
sage: k5.defining_polynomial()
x^4 + x^3 + x^2 + x + 1
sage: y = polygen(QQ,'y')
sage: k.<a> = NumberField(y^9 - 3*y + 5); k
Number Field in a with defining polynomial y^9 - 3*y + 5
sage: k.defining_polynomial()
y^9 - 3*y + 5
Return the degree of this number field.
EXAMPLES:
sage: NumberField(x^3 + x^2 + 997*x + 1, 'a').degree()
3
sage: NumberField(x + 1, 'a').degree()
1
sage: NumberField(x^997 + 17*x + 3, 'a', check=False).degree()
997
Compute the different fractional ideal of this number field.
The codifferent is the fractional ideal of all  in
in  such that the the trace of
such that the the trace of 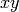 is an integer for
all
is an integer for
all 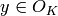 .
.
The different is the integral ideal which is the inverse of the codifferent.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: d = k.different()
sage: d # random sign in output
Fractional ideal (-a)
sage: d.norm()
23
sage: k.disc()
-23
The different is cached:
sage: d is k.different()
True
Another example:
sage: k.<b> = NumberField(x^2 - 123)
sage: d = k.different(); d
Fractional ideal (2*b)
sage: d.norm()
492
sage: k.disc()
492
Shortcut for self.discriminant.
EXAMPLES:
sage: k.<b> = NumberField(x^2 - 123)
sage: k.disc()
492
Returns the discriminant of the ring of integers of the number field, or if v is specified, the determinant of the trace pairing on the elements of the list v.
INPUT:
OUTPUT: Integer if v is omitted, and Rational otherwise.
EXAMPLES:
sage: K.<t> = NumberField(x^3 + x^2 - 2*x + 8)
sage: K.disc()
-503
sage: K.disc([1, t, t^2])
-2012
sage: K.disc([1/7, (1/5)*t, (1/3)*t^2])
-2012/11025
sage: (5*7*3)^2
11025
Return a list of solutions modulo units of positive norm to
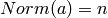 , where a can be any integer in this number
field.
, where a can be any integer in this number
field.
INPUT:
EXAMPLES:
sage: K.<a> = NumberField(x^2+1)
sage: K.elements_of_norm(3)
[]
sage: K.elements_of_norm(50)
[7*a - 1, -5*a + 5, a - 7] # 32-bit
[7*a - 1, -5*a + 5, -7*a - 1] # 64-bit
Return the relative extension of this field by a given polynomial.
EXAMPLES:
sage: K.<a> = NumberField(x^3 - 2)
sage: R.<t> = K[]
sage: L.<b> = K.extension(t^2 + a); L
Number Field in b with defining polynomial t^2 + a over its base field
We create another extension.
sage: k.<a> = NumberField(x^2 + 1); k
Number Field in a with defining polynomial x^2 + 1
sage: y = var('y')
sage: m.<b> = k.extension(y^2 + 2); m
Number Field in b with defining polynomial y^2 + 2 over its base field
Note that b is a root of 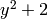 :
:
sage: b.minpoly()
x^2 + 2
sage: b.minpoly('z')
z^2 + 2
A relative extension of a relative extension.
sage: k.<a> = NumberField([x^2 + 1, x^3 + x + 1])
sage: R.<z> = k[]
sage: L.<b> = NumberField(z^3 + 3 + a); L
Number Field in b with defining polynomial z^3 + a0 + 3 over its base field
Ideal factorization of the principal ideal generated by  .
.
EXAMPLE: Here we show how to factor Gaussian integers (up to units).
First we form a number field defined by 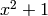 :
:
sage: K.<I> = NumberField(x^2 + 1); K
Number Field in I with defining polynomial x^2 + 1
Here are the factors:
sage: fi, fj = K.factor(13); fi,fj
((Fractional ideal (-3*I - 2), 1), (Fractional ideal (3*I - 2), 1))
Now we extract the reduced form of the generators:
sage: zi = fi[0].gens_reduced()[0]; zi
-3*I - 2
sage: zj = fj[0].gens_reduced()[0]; zj
3*I - 2
We recover the integer that was factored in ![\ZZ[i]](../../../_images/math/0804e0e7b83cafcf84a0606c92c26c327125e125.png) :
:
sage: zi*zj
13
We can see units are not considered:
sage: K.factor(2)
(Fractional ideal (I + 1))^2
sage: expand((I+1)^2)
2*I
One can also factor elements or ideals of the number field:
sage: K.<a> = NumberField(x^2 + 1)
sage: K.factor(1/3)
Fractional ideal (3)^-1
sage: K.factor(1+a)
Fractional ideal (a + 1)
sage: K.factor(1+a/5)
(Fractional ideal (-3*a - 2)) * (Fractional ideal (a + 1)) * (Fractional ideal (-a - 2))^-1 * (Fractional ideal (2*a + 1))^-1
The slightly odd syntax in the next example is to ensure the same result with both 32- and 64-bit systems.
sage: L.<b> = K.extension(x^2 - 7)
sage: list(L.factor(a + 1)) == [(L.ideal((a + b + 2)/2), 1), (L.ideal((a - b - 2)/2), 1)]
True
It doesn’t make sense to factor the ideal (0), so this raises an error:
sage: L.factor(0)
...
AttributeError: 'NumberFieldIdeal' object has no attribute 'factor'
AUTHORS:
Return the ideal in 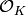 generated by gens.
This overrides the sage.rings.ring.Field method to
use the sage.rings.ring.Ring one instead, since
we’re not really concerned with ideals in a field but in its ring
of integers.
generated by gens.
This overrides the sage.rings.ring.Field method to
use the sage.rings.ring.Ring one instead, since
we’re not really concerned with ideals in a field but in its ring
of integers.
INPUT:
EXAMPLES:
sage: K.<a> = NumberField(x^3-2)
sage: K.fractional_ideal([1/a])
Fractional ideal (1/2*a^2)
One can also input a number field ideal itself, or, more usefully, for a tower of number fields an ideal in one of the fields lower down the tower.
sage: K.fractional_ideal(K.ideal(a))
Fractional ideal (a)
sage: L.<b> = K.extension(x^2 - 3, x^2 + 1)
sage: M.<c> = L.extension(x^2 + 1)
sage: L.ideal(K.ideal(2, a))
Fractional ideal (a)
sage: M.ideal(K.ideal(2, a)) == M.ideal(a*(b - c)/2)
True
The zero ideal is not a fractional ideal!
sage: K.fractional_ideal(0)
...
ValueError: gens must have a nonzero element (zero ideal is not a fractional ideal)
Return the Galois group of the Galois closure of this number field.
INPUT:
Note that computing Galois groups as abstract groups is often much
faster than computing them as explicit automorphism groups (but of
course you get less information out!) For more (important!)
documentation, so the documentation for Galois groups of polynomials
over  , e.g., by typing K.polynomial().galois_group?,
where
, e.g., by typing K.polynomial().galois_group?,
where  is a number field.
is a number field.
To obtain actual field homomorphisms from the number field to its splitting field, use type=None.
EXAMPLES:
With type None:
sage: k.<b> = NumberField(x^2 - 14) # a Galois extension
sage: G = k.galois_group(); G
Galois group of Number Field in b with defining polynomial x^2 - 14
sage: G.gen(0)
(1,2)
sage: G.gen(0)(b)
-b
sage: G.artin_symbol(k.primes_above(3)[0])
(1,2)
sage: k.<b> = NumberField(x^3 - x + 1) # not Galois
sage: G = k.galois_group(names='c'); G
Galois group of Galois closure in c of Number Field in b with defining polynomial x^3 - x + 1
sage: G.gen(0)
(1,2)(3,5)(4,6)
With type 'pari':
sage: NumberField(x^3-2, 'a').galois_group(type="pari")
Galois group PARI group [6, -1, 2, "S3"] of degree 3 of the Number Field in a with defining polynomial x^3 - 2
sage: NumberField(x-1, 'a').galois_group(type="gap") # optional - database_gap
Galois group Transitive group number 1 of degree 1 of the Number Field in a with defining polynomial x - 1
sage: NumberField(x^2+2, 'a').galois_group(type="gap") # optional - database_gap
Galois group Transitive group number 1 of degree 2 of the Number Field in a with defining polynomial x^2 + 2
sage: NumberField(x^3-2, 'a').galois_group(type="gap") # optional - database_gap
Galois group Transitive group number 2 of degree 3 of the Number Field in a with defining polynomial x^3 - 2
sage: x = polygen(QQ)
sage: NumberField(x^3 + 2*x + 1, 'a').galois_group(pari_group=False) # optional - database_gap
Galois group Transitive group number 2 of degree 3 of the Number Field in a with defining polynomial x^3 + 2*x + 1
sage: NumberField(x^3 + 2*x + 1, 'a').galois_group(algorithm='magma') # optional - magma, , database_gap
Galois group Transitive group number 2 of degree 3 of the Number Field in a with defining polynomial x^3 + 2*x + 1
EXPLICIT GALOIS GROUP: We compute the Galois group as an explicit group of automorphisms of the Galois closure of a field.
sage: K.<a> = NumberField(x^3 - 2)
sage: L.<b1> = K.galois_closure(); L
Number Field in b1 with defining polynomial x^6 + 40*x^3 + 1372
sage: G = End(L); G
Automorphism group of Number Field in b1 with defining polynomial x^6 + 40*x^3 + 1372
sage: G.list()
[
Ring endomorphism of Number Field in b1 with defining polynomial x^6 + 40*x^3 + 1372
Defn: b1 |--> b1,
...
Ring endomorphism of Number Field in b1 with defining polynomial x^6 + 40*x^3 + 1372
Defn: b1 |--> -2/63*b1^4 - 31/63*b1
]
sage: G[1](b1)
1/36*b1^4 + 1/18*b1
Return the generator for this number field.
INPUT:
EXAMPLES:
sage: k.<theta> = NumberField(x^14 + 2); k
Number Field in theta with defining polynomial x^14 + 2
sage: k.gen()
theta
sage: k.gen(1)
...
IndexError: Only one generator.
If an embedding has been specified, return the image of the generator under that embedding. Otherwise return None.
EXAMPLES:
sage: QuadraticField(-7, 'a').gen_embedding()
2.645751311064591?*I
sage: NumberField(x^2+7, 'a').gen_embedding() # None
K.ideal() returns a fractional ideal of the field, except for the zero ideal which is not a fractional ideal.
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: K.ideal(2)
Fractional ideal (2)
sage: K.ideal(2+i)
Fractional ideal (i + 2)
sage: K.ideal(0)
Ideal (0) of Number Field in i with defining polynomial x^2 + 1
All integral ideals of bounded norm.
INPUT:
OUTPUT: A dict of all integral ideals I such that Norm(I) <= bound, keyed by norm.
EXAMPLE:
sage: K.<a> = NumberField(x^2 + 23)
sage: d = K.ideals_of_bdd_norm(10)
sage: for n in d:
... print n
... for I in d[n]:
... print I
1
Fractional ideal (1)
2
Fractional ideal (2, 1/2*a - 1/2)
Fractional ideal (2, 1/2*a + 1/2)
3
Fractional ideal (3, -1/2*a + 1/2)
Fractional ideal (3, -1/2*a - 1/2)
4
Fractional ideal (4, 1/2*a + 3/2)
Fractional ideal (2)
Fractional ideal (4, 1/2*a + 5/2)
5
6
Fractional ideal (-1/2*a + 1/2)
Fractional ideal (6, 1/2*a + 5/2)
Fractional ideal (6, 1/2*a + 7/2)
Fractional ideal (1/2*a + 1/2)
7
8
Fractional ideal (-1/2*a - 3/2)
Fractional ideal (4, a - 1)
Fractional ideal (4, a + 1)
Fractional ideal (1/2*a - 3/2)
9
Fractional ideal (9, 1/2*a + 11/2)
Fractional ideal (3)
Fractional ideal (9, 1/2*a + 7/2)
10
Returns a list containing a ZZ-basis for the full ring of integers of this number field.
INPUT:
EXAMPLES:
sage: K.<a> = NumberField(x^5 + 10*x + 1)
sage: K.integral_basis()
[1, a, a^2, a^3, a^4]
Next we compute the ring of integers of a cubic field in which 2 is an “essential discriminant divisor”, so the ring of integers is not generated by a single element.
sage: K.<a> = NumberField(x^3 + x^2 - 2*x + 8)
sage: K.integral_basis()
[1, 1/2*a^2 + 1/2*a, a^2]
ALGORITHM: Uses the pari library.
Returns True if self is an absolute field.
This function will be implemented in the derived classes.
EXAMPLES:
sage: K = CyclotomicField(5)
sage: K.is_absolute()
True
Return True since a number field is a field.
EXAMPLES:
sage: NumberField(x^5 + x + 3, 'c').is_field()
True
Return True if this number field is a Galois extension of
 .
.
EXAMPLES:
sage: NumberField(x^2 + 1, 'i').is_galois()
True
sage: NumberField(x^3 + 2, 'a').is_galois()
False
Return True if self is isomorphic as a number field to other.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 1)
sage: m.<b> = NumberField(x^2 + 4)
sage: k.is_isomorphic(m)
True
sage: m.<b> = NumberField(x^2 + 5)
sage: k.is_isomorphic (m)
False
sage: k = NumberField(x^3 + 2, 'a')
sage: k.is_isomorphic(NumberField((x+1/3)^3 + 2, 'b'))
True
sage: k.is_isomorphic(NumberField(x^3 + 4, 'b'))
True
sage: k.is_isomorphic(NumberField(x^3 + 5, 'b'))
False
EXAMPLES:
sage: K.<a> = NumberField(x^10 - 2)
sage: K.is_absolute()
True
sage: K.is_relative()
False
Return True if self is totally imaginary, and False otherwise.
Totally imaginary means that no isomorphic embedding of self into the complex numbers has image contained in the real numbers.
EXAMPLES:
sage: NumberField(x^2+2, 'alpha').is_totally_imaginary()
True
sage: NumberField(x^2-2, 'alpha').is_totally_imaginary()
False
sage: NumberField(x^4-2, 'alpha').is_totally_imaginary()
False
Return True if self is totally real, and False otherwise.
Totally real means that every isomorphic embedding of self into the complex numbers has image contained in the real numbers.
EXAMPLES:
sage: NumberField(x^2+2, 'alpha').is_totally_real()
False
sage: NumberField(x^2-2, 'alpha').is_totally_real()
True
sage: NumberField(x^4-2, 'alpha').is_totally_real()
False
Return the latex representation of the variable name for this number field.
EXAMPLES:
sage: NumberField(x^2 + 3, 'a').latex_variable_name()
'a'
sage: NumberField(x^3 + 3, 'theta3').latex_variable_name()
'\theta_{3}'
sage: CyclotomicField(5).latex_variable_name()
'\zeta_{5}'
Return the narrow class group of this field.
INPUT:
EXAMPLES:
sage: NumberField(x^3+x+9, 'a').narrow_class_group()
Multiplicative Abelian Group isomorphic to C2
Return the number of generators of this number field (always 1).
OUTPUT: the python integer 1.
EXAMPLES:
sage: NumberField(x^2 + 17,'a').ngens()
1
sage: NumberField(x + 3,'a').ngens()
1
sage: k.<a> = NumberField(x + 3)
sage: k.ngens()
1
sage: k.0
-3
Return the number of roots of unity in this field.
Note
We do not create the full unit group since that can be expensive, but we do use it if it is already known.
EXAMPLES:
sage: F.<alpha> = NumberField(x**22+3)
sage: F.zeta_order()
6
sage: F.<alpha> = NumberField(x**2-7)
sage: F.zeta_order()
2
Return the order of this number field (always +infinity).
OUTPUT: always positive infinity
EXAMPLES:
sage: NumberField(x^2 + 19,'a').order()
+Infinity
PARI big number field corresponding to this field.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 1); k
Number Field in a with defining polynomial x^2 + 1
sage: len(k.pari_bnf())
10
sage: k.pari_bnf()[:4]
[[;], matrix(0,7), [;], ...]
sage: len(k.pari_nf())
9
Run the PARI bnfcertify function to ensure the correctness of answers.
If this function returns True (and doesn’t raise a ValueError), then certification succeeded, and results that use the PARI bnf structure with this field are supposed to be correct.
Warning
I wouldn’t trust this to mean that everything computed involving this number field is actually correct.
EXAMPLES:
sage: k.<a> = NumberField(x^7 + 7); k
Number Field in a with defining polynomial x^7 + 7
sage: k.pari_bnf_certify()
True
PARI number field corresponding to this field.
This is the number field constructed using nfinit. This is the same as the number field got by doing pari(self) or gp(self).
EXAMPLES:
sage: k.<a> = NumberField(x^4 - 3*x + 7); k
Number Field in a with defining polynomial x^4 - 3*x + 7
sage: k.pari_nf()[:4]
[x^4 - 3*x + 7, [0, 2], 85621, 1]
sage: pari(k)[:4]
[x^4 - 3*x + 7, [0, 2], 85621, 1]
sage: k.<a> = NumberField(x^4 - 3/2*x + 5/3); k
Number Field in a with defining polynomial x^4 - 3/2*x + 5/3
sage: k.pari_nf()
...
TypeError: Unable to coerce number field defined by non-integral polynomial to PARI.
sage: pari(k)
...
TypeError: Unable to coerce number field defined by non-integral polynomial to PARI.
sage: gp(k)
...
TypeError: Unable to coerce number field defined by non-integral polynomial to PARI.
PARI polynomial corresponding to polynomial that defines this field. By default, this is a polynomial in the variable “x”.
EXAMPLES:
sage: y = polygen(QQ)
sage: k.<a> = NumberField(y^2 - 3/2*y + 5/3)
sage: k.pari_polynomial()
x^2 - 3/2*x + 5/3
sage: k.pari_polynomial('a')
a^2 - 3/2*a + 5/3
Return the defining polynomial of this number field.
This is exactly the same as self.defining_polynomal().
EXAMPLES:
sage: NumberField(x^2 + (2/3)*x - 9/17,'a').polynomial()
x^2 + 2/3*x - 9/17
Return defining polynomial of this number field as a pair, an ntl polynomial and a denominator.
This is used mainly to implement some internal arithmetic.
EXAMPLES:
sage: NumberField(x^2 + (2/3)*x - 9/17,'a').polynomial_ntl()
([-27 34 51], 51)
Return the polynomial quotient ring isomorphic to this number field.
EXAMPLES:
sage: K = NumberField(x^3 + 2*x - 5, 'alpha')
sage: K.polynomial_quotient_ring()
Univariate Quotient Polynomial Ring in alpha over Rational Field with modulus x^3 + 2*x - 5
Return the polynomial ring that we view this number field as being a quotient of (by a principal ideal).
EXAMPLES: An example with an absolute field:
sage: k.<a> = NumberField(x^2 + 3)
sage: y = polygen(QQ, 'y')
sage: k.<a> = NumberField(y^2 + 3)
sage: k.polynomial_ring()
Univariate Polynomial Ring in y over Rational Field
An example with a relative field:
sage: y = polygen(QQ, 'y')
sage: M.<a> = NumberField([y^3 + 97, y^2 + 1]); M
Number Field in a0 with defining polynomial y^3 + 97 over its base field
sage: M.polynomial_ring()
Univariate Polynomial Ring in y over Number Field in a1 with defining polynomial y^2 + 1
Return a power basis for this number field over its base field.
If this number field is represented as ![k[t]/f(t)](../../../_images/math/ea5c5384b0cd9fd5f7d31eca4f469fe62d18b683.png) , then
the basis returned is
, then
the basis returned is  where
where
 is the degree of this number field over its base
field.
is the degree of this number field over its base
field.
EXAMPLES:
sage: K.<a> = NumberField(x^5 + 10*x + 1)
sage: K.power_basis()
[1, a, a^2, a^3, a^4]
sage: L.<b> = K.extension(x^2 - 2)
sage: L.power_basis()
[1, b]
sage: L.absolute_field('c').power_basis()
[1, c, c^2, c^3, c^4, c^5, c^6, c^7, c^8, c^9]
sage: M = CyclotomicField(15)
sage: M.power_basis()
[1, zeta15, zeta15^2, zeta15^3, zeta15^4, zeta15^5, zeta15^6, zeta15^7]
Return a prime ideal of self lying over x.
INPUT:
OUTPUT: A prime ideal of self lying over x. If degree is specified and no such ideal exists, raises a ValueError.
EXAMPLES:
sage: x = ZZ['x'].gen()
sage: F.<t> = NumberField(x^3 - 2)
sage: P2 = F.prime_above(2)
sage: P2 # random
Fractional ideal (-t)
sage: 2 in P2
True
sage: P2.is_prime()
True
sage: P2.norm()
2
sage: P3 = F.prime_above(3)
sage: P3 # random
Fractional ideal (t + 1)
sage: 3 in P3
True
sage: P3.is_prime()
True
sage: P3.norm()
3
The ideal (3) is totally ramified in F, so there is no degree 2 prime above 3:
sage: F.prime_above(3, degree=2)
...
ValueError: No prime of degree 2 above Fractional ideal (3)
sage: [ id.residue_class_degree() for id, _ in F.ideal(3).factor() ]
[1]
Asking for a specific degree works:
sage: P5_1 = F.prime_above(5, degree=1)
sage: P5_1 # random
Fractional ideal (-t^2 - 1)
sage: P5_1.residue_class_degree()
1
sage: P5_2 = F.prime_above(5, degree=2)
sage: P5_2 # random
Fractional ideal (t^2 - 2*t - 1)
sage: P5_2.residue_class_degree()
2
Relative number fields are ok:
sage: G = F.extension(x^2 - 11, 'b')
sage: G.prime_above(7)
Fractional ideal (b + 2)
It doesn’t make sense to factor the ideal (0):
sage: F.prime_above(0)
...
AttributeError: 'NumberFieldIdeal' object has no attribute 'prime_factors'
Return a list of the prime ideals of self which divide
the ideal generated by  .
.
OUTPUT: list of prime ideals (a new list is returned each time this function is called)
EXAMPLES:
sage: K.<w> = NumberField(x^2 + 23)
sage: K.prime_factors(w + 1)
[Fractional ideal (2, 1/2*w - 1/2),
Fractional ideal (2, 1/2*w + 1/2),
Fractional ideal (3, -1/2*w - 1/2)]
Return prime ideals of self lying over x.
INPUT:
OUTPUT: A list of prime ideals of self lying over x. If degree is specified and no such ideal exists, returns the empty list. The output is sorted by residue degree first, then by underlying prime (or equivalently, by norm).
EXAMPLES:
sage: x = ZZ['x'].gen()
sage: F.<t> = NumberField(x^3 - 2)
sage: P2s = F.primes_above(2)
sage: P2s # random
[Fractional ideal (-t)]
sage: all(2 in P2 for P2 in P2s)
True
sage: all(P2.is_prime() for P2 in P2s)
True
sage: [ P2.norm() for P2 in P2s ]
[2]
sage: P3s = F.primes_above(3)
sage: P3s # random
[Fractional ideal (t + 1)]
sage: all(3 in P3 for P3 in P3s)
True
sage: all(P3.is_prime() for P3 in P3s)
True
sage: [ P3.norm() for P3 in P3s ]
[3]
The ideal (3) is totally ramified in F, so there is no degree 2 prime above 3:
sage: F.primes_above(3, degree=2)
[]
sage: [ id.residue_class_degree() for id, _ in F.ideal(3).factor() ]
[1]
Asking for a specific degree works:
sage: P5_1s = F.primes_above(5, degree=1)
sage: P5_1s # random
[Fractional ideal (-t^2 - 1)]
sage: P5_1 = P5_1s[0]; P5_1.residue_class_degree()
1
sage: P5_2s = F.primes_above(5, degree=2)
sage: P5_2s # random
[Fractional ideal (t^2 - 2*t - 1)]
sage: P5_2 = P5_2s[0]; P5_2.residue_class_degree()
2
Works in relative extensions too:
sage: PQ.<X> = QQ[]
sage: F.<a, b> = NumberField([X^2 - 2, X^2 - 3])
sage: PF.<Y> = F[]
sage: K.<c> = F.extension(Y^2 - (1 + a)*(a + b)*a*b)
sage: I = F.ideal(a + 2*b)
sage: P, Q = K.primes_above(I)
sage: K.ideal(I) == P^4*Q
True
sage: K.primes_above(I, degree=1) == [P]
True
sage: K.primes_above(I, degree=4) == [Q]
True
It doesn’t make sense to factor the ideal (0), so this raises an error:
sage: F.prime_above(0)
...
AttributeError: 'NumberFieldIdeal' object has no attribute 'prime_factors'
Return an iterator yielding prime ideals of absolute degree one and small norm.
Warning
It is possible that there are no primes of  of
absolute degree one of small prime norm, and it possible
that this algorithm will not find any primes of small norm.
of
absolute degree one of small prime norm, and it possible
that this algorithm will not find any primes of small norm.
See module sage.rings.number_field.small_primes_of_degree_one for details.
INPUT:
EXAMPLES:
sage: K.<z> = CyclotomicField(10)
sage: it = K.primes_of_degree_one_iter()
sage: Ps = [ it.next() for i in range(3) ]
sage: Ps # random
[Fractional ideal (z^3 + z + 1), Fractional ideal (3*z^3 - z^2 + z - 1), Fractional ideal (2*z^3 - 3*z^2 + z - 2)]
sage: [ P.norm() for P in Ps ] # random
[11, 31, 41]
sage: [ P.residue_class_degree() for P in Ps ]
[1, 1, 1]
Return a list of n prime ideals of absolute degree one and small norm.
Warning
It is possible that there are no primes of  of
absolute degree one of small prime norm, and it possible
that this algorithm will not find any primes of small norm.
of
absolute degree one of small prime norm, and it possible
that this algorithm will not find any primes of small norm.
See module sage.rings.number_field.small_primes_of_degree_one for details.
INPUT:
EXAMPLES:
sage: K.<z> = CyclotomicField(10)
sage: Ps = K.primes_of_degree_one_list(3)
sage: Ps
[Fractional ideal (z^3 + z + 1), Fractional ideal (3*z^3 - z^2 + z - 1), Fractional ideal (2*z^3 - 3*z^2 + z - 2)]
sage: [ P.norm() for P in Ps ]
[11, 31, 41]
sage: [ P.residue_class_degree() for P in Ps ]
[1, 1, 1]
Return a primitive element for this field, i.e., an element that
generates it over  .
.
EXAMPLES:
sage: K.<a> = NumberField(x^3 + 2)
sage: K.primitive_element()
a
sage: K.<a,b,c> = NumberField([x^2-2,x^2-3,x^2-5])
sage: K.primitive_element()
a - b + c
sage: alpha = K.primitive_element(); alpha
a - b + c
sage: alpha.minpoly()
x^2 + (2*b - 2*c)*x - 2*c*b + 6
sage: alpha.absolute_minpoly()
x^8 - 40*x^6 + 352*x^4 - 960*x^2 + 576
Return a generator of the roots of unity in this field.
Note
We do not create the full unit group since that can be expensive, but we do use it if it is already known.
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: z = K.primitive_root_of_unity(); z
i
sage: z.multiplicative_order()
4
sage: K.<a> = NumberField(x^2+x+1)
sage: z = K.primitive_root_of_unity(); z
-a
sage: z.multiplicative_order()
6
Return a random element of this number field.
INPUT:
the resulting element
of the resulting element
the resulting element will have integral
coefficients. This option overrides any
value of  .
.
of the resulting element
OUTPUT:
EXAMPLES:
sage: K.<j> = NumberField(x^8+1)
sage: K.random_element()
1/2*j^7 - j^6 - 12*j^5 + 1/2*j^4 - 1/95*j^3 - 1/2*j^2 - 4
sage: K.<a,b,c> = NumberField([x^2-2,x^2-3,x^2-5])
sage: K.random_element()
((6136*c - 7489/3)*b + 5825/3*c - 71422/3)*a + (-4849/3*c + 58918/3)*b - 45718/3*c + 75409/12
sage: K.<a> = NumberField(x^5-2)
sage: K.random_element(integral_coefficients=True)
a^3 + a^2 - 3*a - 1
Return all homomorphisms of this number field into the approximate real field with precision prec.
If prec is 53 (the default), then the real double field is used; otherwise the arbitrary precision (but slow) real field is used. If you want embeddings into the 53-bit double precision, which is faster, use self.embeddings(RDF).
EXAMPLES:
sage: K.<a> = NumberField(x^3 + 2)
sage: K.real_embeddings()
[
Ring morphism:
From: Number Field in a with defining polynomial x^3 + 2
To: Real Field with 53 bits of precision
Defn: a |--> -1.25992104989487
]
sage: K.real_embeddings(16)
[
Ring morphism:
From: Number Field in a with defining polynomial x^3 + 2
To: Real Field with 16 bits of precision
Defn: a |--> -1.260
]
sage: K.real_embeddings(100)
[
Ring morphism:
From: Number Field in a with defining polynomial x^3 + 2
To: Real Field with 100 bits of precision
Defn: a |--> -1.2599210498948731647672106073
]
This function returns an LLL-reduced basis for the Minkowski-embedding of the maximal order of a number field.
INPUT:
OUTPUT:
An LLL-reduced basis for the Minkowski-embedding of the maximal order of a number field, given by a sequence of (integral) elements from the field.
Note
In the non-totally-real case, the LLL routine we call is currently Pari’s qflll(), which works with floating point approximations, and so the result is only as good as the precision promised by Pari. The matrix returned will always be integral; however, it may only be only “almost” LLL-reduced when the precision is not sufficiently high.
If the following run-time error occurs: “PariError: not a definite matrix in lllgram (42)” try increasing the prec parameter,
EXAMPLES:
sage: F.<t> = NumberField(x^6-7*x^4-x^3+11*x^2+x-1)
sage: F.maximal_order().basis()
[1/2*t^5 + 1/2*t^4 + 1/2*t^2 + 1/2, t, t^2, t^3, t^4, t^5]
sage: F.reduced_basis()
[-1, -1/2*t^5 + 1/2*t^4 + 3*t^3 - 3/2*t^2 - 4*t - 1/2, t, 1/2*t^5 + 1/2*t^4 - 4*t^3 - 5/2*t^2 + 7*t + 1/2, 1/2*t^5 - 1/2*t^4 - 2*t^3 + 3/2*t^2 - 1/2, 1/2*t^5 - 1/2*t^4 - 3*t^3 + 5/2*t^2 + 4*t - 5/2]
sage: CyclotomicField(12).reduced_basis()
[1, zeta12^2, zeta12, zeta12^3]
sage: F.<alpha> = NumberField(x^4+x^2+712312*x+131001238)
sage: F.integral_basis()
[1, alpha, 1/2*alpha^3 + 1/2*alpha^2, alpha^3]
sage: F.reduced_basis(prec=64)
[1, alpha, alpha^3 - 2*alpha^2 + 15*alpha, 16*alpha^3 - 31*alpha^2 + 469*alpha + 267109] # 32-bit
... # 64-bit
PariError: not a definite matrix in lllgram (42) # 64-bit
sage: F.reduced_basis(prec=96)
[1, alpha, alpha^3 - 2*alpha^2 + 15*alpha, 16*alpha^3 - 31*alpha^2 + 469*alpha + 267109]
This function returns the Gram matrix of an LLL-reduced basis for the Minkowski embedding of the maximal order of a number field.
INPUT:
OUTPUT: The Gram matrix ![[<x_i,x_j>]](../../../_images/math/61facfab51c22d84b851849e18eef65417d40d05.png) of an LLL reduced
basis for the maximal order of self, where the integral basis for
self is given by
of an LLL reduced
basis for the maximal order of self, where the integral basis for
self is given by 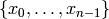 . Here < , > is the
usual inner product on
. Here < , > is the
usual inner product on 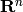 , and self is embedded in
, and self is embedded in
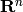 by the Minkowski embedding. See the docstring for
Minkowski_embedding() for more information.
by the Minkowski embedding. See the docstring for
Minkowski_embedding() for more information.
Note
In the non-totally-real case, the LLL routine we call is currently Pari’s qflll(), which works with floating point approximations, and so the result is only as good as the precision promised by Pari. In particular, in this case, the returned matrix will not be integral, and may not have enough precision to recover the correct gram matrix (which is known to be integral for theoretical reasons). Thus the need for the prec flag above.
If the following run-time error occurs: “PariError: not a definite matrix in lllgram (42)” try increasing the prec parameter,
EXAMPLES:
sage: F.<t> = NumberField(x^6-7*x^4-x^3+11*x^2+x-1)
sage: F.reduced_gram_matrix()
[ 6 3 0 2 0 1]
[ 3 9 0 1 0 -2]
[ 0 0 14 6 -2 3]
[ 2 1 6 16 -3 3]
[ 0 0 -2 -3 16 6]
[ 1 -2 3 3 6 19]
sage: Matrix(6, [(x*y).trace() for x in F.integral_basis() for y in F.integral_basis()])
[2550 133 259 664 1368 3421]
[ 133 14 3 54 30 233]
[ 259 3 54 30 233 217]
[ 664 54 30 233 217 1078]
[1368 30 233 217 1078 1371]
[3421 233 217 1078 1371 5224]
sage: var('x')
x
sage: F.<alpha> = NumberField(x^4+x^2+712312*x+131001238)
sage: F.reduced_gram_matrix(prec=128)
[ 4.0000000000000000000000000000000000000 0.00000000000000000000000000000000000000 -2.1369320000000000000000000000000000000e6 -3.3122478000000000000000000000000000000e7]
[ 0.00000000000000000000000000000000000000 46721.539331563218381658483353092335550 -2.2467769057394530109094755223395819322e7 -3.4807276041138450473611629088647496430e8]
[-2.1369320000000000000000000000000000000e6 -2.2467769057394530109094755223395819322e7 7.0704243186034907491782135494859351061e12 1.1256636615786237006027526953641297995e14]
[-3.3122478000000000000000000000000000000e7 -3.4807276041138450473611629088647496430e8 1.1256636615786237006027526953641297995e14 1.7923838231014970520503146603069479547e15]
Return the regulator of this number field.
Note that PARI computes the regulator to higher precision than the Sage default.
INPUT:
EXAMPLES:
sage: NumberField(x^2-2, 'a').regulator()
0.881373587019543
sage: NumberField(x^4+x^3+x^2+x+1, 'a').regulator()
0.962423650119207
Return the residue field of this number field at a given prime, ie
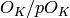 .
.
INPUT:
OUTPUT: The residue field at this prime.
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^4+3*x^2-17)
sage: P = K.ideal(61).factor()[0][0]
sage: K.residue_field(P)
Residue field in abar of Fractional ideal (-2*a^2 + 1)
sage: K.<i> = NumberField(x^2 + 1)
sage: K.residue_field(1+i)
Residue field of Fractional ideal (i + 1)
TESTS:
sage: L.<b> = NumberField(x^2 + 5)
sage: L.residue_field(P)
...
ValueError: Fractional ideal (-2*a^2 + 1) is not an ideal of Number Field in b with defining polynomial x^2 + 5
sage: L.residue_field(2)
...
ValueError: Fractional ideal (2) is not a prime ideal
sage: L.residue_field(L.prime_above(5)^2)
...
ValueError: Fractional ideal (5) is not a prime ideal
Return all the roots of unity in this field, primitive or not.
EXAMPLES:
sage: K.<b> = NumberField(x^2+1)
sage: zs = K.roots_of_unity(); zs
[b, -1, -b, 1]
sage: [ z**K.number_of_roots_of_unity() for z in zs ]
[1, 1, 1, 1]
Compute the Selmer group 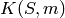 , which is defined to be the subgroup of
, which is defined to be the subgroup of
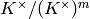 consisting of elements
consisting of elements  such that
such that
![K(\sqrt[m]{a})/K](../../../_images/math/2951092327cfa807343916fd380a6eb9c3285608.png) is unramified at all primes of
is unramified at all primes of  lying above a
place outside of
lying above a
place outside of  .
.
INPUT:
OUTPUT:
A list of generators of 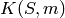 .
.
EXAMPLES:
sage: K.<a> = QuadraticField(-5)
sage: K.selmer_group((), 2)
[-1, 2]
sage: K.selmer_group([K.ideal(2, -a+1)], 2)
[2, -1]
sage: K.selmer_group([K.ideal(2, -a+1), K.ideal(3, a+1)], 2)
[2, a + 1, -1]
sage: K.selmer_group((K.ideal(2, -a+1),K.ideal(3, a+1)), 4)
[2, a + 1, -1]
sage: K.selmer_group([K.ideal(2, -a+1)], 3)
[2]
sage: K.selmer_group([K.ideal(2, -a+1), K.ideal(3, a+1)], 3)
[2, a + 1]
sage: K.selmer_group([K.ideal(2, -a+1), K.ideal(3, a+1), K.ideal(a)], 3)
[2, a + 1, -a]
sage: K.<a> = NumberField(polygen(QQ))
sage: K.selmer_group([],5)
[]
Return (r1, r2), where r1 and r2 are the number of real embeddings and pairs of complex embeddings of this field, respectively.
EXAMPLES:
sage: NumberField(x^2+1, 'a').signature()
(0, 1)
sage: NumberField(x^3-2, 'a').signature()
(1, 1)
Returns the embedding of this field into the complex numbers which has been specified.
Fields created with the QuadraticField or CyclotomicField constructors come with an implicit embedding. To get one of these fields without the embedding, use the generic NumberField constructor.
EXAMPLES:
sage: QuadraticField(-1, 'I').specified_complex_embedding()
Generic morphism:
From: Number Field in I with defining polynomial x^2 + 1
To: Complex Lazy Field
Defn: I -> 1*I
sage: QuadraticField(3, 'a').specified_complex_embedding()
Generic morphism:
From: Number Field in a with defining polynomial x^2 - 3
To: Real Lazy Field
Defn: a -> 1.732050807568878?
sage: CyclotomicField(13).specified_complex_embedding()
Generic morphism:
From: Cyclotomic Field of order 13 and degree 12
To: Complex Lazy Field
Defn: zeta13 -> 0.885456025653210? + 0.464723172043769?*I
Most fields don’t implicitly have embeddings unless explicitly specified:
sage: NumberField(x^2-2, 'a').specified_complex_embedding() is None
True
sage: NumberField(x^3-x+5, 'a').specified_complex_embedding() is None
True
sage: NumberField(x^3-x+5, 'a', embedding=2).specified_complex_embedding()
Generic morphism:
From: Number Field in a with defining polynomial x^3 - x + 5
To: Real Lazy Field
Defn: a -> -1.904160859134921?
sage: NumberField(x^3-x+5, 'a', embedding=CDF.0).specified_complex_embedding()
Generic morphism:
From: Number Field in a with defining polynomial x^3 - x + 5
To: Complex Lazy Field
Defn: a -> 0.952080429567461? + 1.311248044077123?*I
This function only returns complex embeddings:
sage: K.<a> = NumberField(x^2-2, embedding=Qp(7)(2).sqrt())
sage: K.specified_complex_embedding() is None
True
sage: K.gen_embedding()
3 + 7 + 2*7^2 + 6*7^3 + 7^4 + 2*7^5 + 7^6 + 2*7^7 + 4*7^8 + 6*7^9 + 6*7^10 + 2*7^11 + 7^12 + 7^13 + 2*7^15 + 7^16 + 7^17 + 4*7^18 + 6*7^19 + O(7^20)
sage: K.coerce_embedding()
Generic morphism:
From: Number Field in a with defining polynomial x^2 - 2
To: 7-adic Field with capped relative precision 20
Defn: a -> 3 + 7 + 2*7^2 + 6*7^3 + 7^4 + 2*7^5 + 7^6 + 2*7^7 + 4*7^8 + 6*7^9 + 6*7^10 + 2*7^11 + 7^12 + 7^13 + 2*7^15 + 7^16 + 7^17 + 4*7^18 + 6*7^19 + O(7^20)
Return fixed isomorphism or embedding structure on self.
This is used to record various isomorphisms or embeddings that arise naturally in other constructions.
EXAMPLES:
sage: K.<z> = NumberField(x^2 + 3)
sage: L.<a> = K.absolute_field(); L
Number Field in a with defining polynomial x^2 + 3
sage: L.structure()
(Isomorphism given by variable name change map:
From: Number Field in a with defining polynomial x^2 + 3
To: Number Field in z with defining polynomial x^2 + 3,
Isomorphism given by variable name change map:
From: Number Field in z with defining polynomial x^2 + 3
To: Number Field in a with defining polynomial x^2 + 3)
sage: K.<a> = QuadraticField(-3)
sage: R.<y> = K[]
sage: D.<x0> = K.extension(y)
sage: D_abs.<y0> = D.absolute_field()
sage: D_abs.structure()[0](y0)
-a
Return an absolute number field K isomorphic to QQ(alpha) and a map from K to self that sends the generator of K to alpha.
INPUT:
OUTPUT:
EXAMPLES:
sage: K.<a> = NumberField(x^4 - 3); K
Number Field in a with defining polynomial x^4 - 3
sage: H.<b>, from_H = K.subfield(a^2)
sage: H
Number Field in b with defining polynomial x^2 - 3
sage: from_H(b)
a^2
sage: from_H
Ring morphism:
From: Number Field in b with defining polynomial x^2 - 3
To: Number Field in a with defining polynomial x^4 - 3
Defn: b |--> a^2
sage: K.<z> = CyclotomicField(5)
sage: K.subfield(z-z^2-z^3+z^4)
(Number Field in z0 with defining polynomial x^2 - 5,
Ring morphism:
From: Number Field in z0 with defining polynomial x^2 - 5
To: Cyclotomic Field of order 5 and degree 4
Defn: z0 |--> -2*z^3 - 2*z^2 - 1)
You can also view a number field as having a different generator by just choosing the input to generate the whole field; for that it is better to use self.change_generator, which gives isomorphisms in both directions.
Return the matrix of the trace pairing on the elements of the list
 .
.
EXAMPLES:
sage: K.<zeta3> = NumberField(x^2 + 3)
sage: K.trace_pairing([1,zeta3])
[ 2 0]
[ 0 -6]
Returns an element of self with valuation 1 at the prime ideal P.
INPUT:
Note
When P is principal (e.g. always when self has class number one) the result may or may not be a generator of P!
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 5); K
Number Field in a with defining polynomial x^2 + 5
sage: P,Q = K.ideal(3).prime_factors()
sage: P
Fractional ideal (3, a + 1)
sage: pi=K.uniformizer(P); pi
a + 1
sage: K.ideal(pi).factor()
(Fractional ideal (2, a + 1)) * (Fractional ideal (3, a + 1))
sage: pi=K.uniformizer(P,'negative'); pi
1/2*a + 1/2
sage: K.ideal(pi).factor()
(Fractional ideal (2, a + 1))^-1 * (Fractional ideal (3, a + 1))
sage: K = CyclotomicField(9)
sage: Plist=K.ideal(17).prime_factors()
sage: pilist = [K.uniformizer(P) for P in Plist]
sage: [pi.is_integral() for pi in pilist]
[True, True, True]
sage: [pi.valuation(P) for pi,P in zip(pilist,Plist)]
[1, 1, 1]
sage: [ pilist[i] in Plist[i] for i in range(len(Plist)) ]
[True, True, True]
Return the unit group (including torsion) of this number field.
ALGORITHM: Uses PARI’s bnfunit command.
INPUT:
Note
The group is cached.
EXAMPLES:
sage: x = QQ['x'].0
sage: A = x^4 - 10*x^3 + 20*5*x^2 - 15*5^2*x + 11*5^3
sage: K = NumberField(A, 'a')
sage: U = K.unit_group(); U
Unit group with structure C10 x Z of Number Field in a with defining polynomial x^4 - 10*x^3 + 100*x^2 - 375*x + 1375
sage: U.gens()
[-1/275*a^3 + 7/55*a^2 - 6/11*a + 4, 8/275*a^3 - 12/55*a^2 + 15/11*a - 2]
sage: U.invariants()
[10, 0]
sage: [u.multiplicative_order() for u in U.gens()]
[10, +Infinity]
Sage might not be able to provably compute the unit group:
sage: K = NumberField(x^17 + 3, 'a')
sage: K.unit_group(proof=True) # default
...
PariError: not enough precomputed primes, need primelimit ~ (35)
In this case, one can ask for the conjectural unit group (correct if the Generalized Riemann Hypothesis is true):
sage: U = K.unit_group(proof=False); U; U.gens()
Unit group with structure C2 x Z x Z x Z x Z x Z x Z x Z x Z of Number Field in a with defining polynomial x^17 + 3
[-1,
a^9 + a - 1,
a^16 - a^15 + a^14 - a^12 + a^11 - a^10 - a^8 + a^7 - 2*a^6 + a^4 - 3*a^3 + 2*a^2 - 2*a + 1,
2*a^16 - a^14 - a^13 + 3*a^12 - 2*a^10 + a^9 + 3*a^8 - 3*a^6 + 3*a^5 + 3*a^4 - 2*a^3 - 2*a^2 + 3*a + 4,
2*a^16 - 3*a^15 + 3*a^14 - 3*a^13 + 3*a^12 - a^11 + a^9 - 3*a^8 + 4*a^7 - 5*a^6 + 6*a^5 - 4*a^4 + 3*a^3 - 2*a^2 - 2*a + 4,
a^15 - a^12 + a^10 - a^9 - 2*a^8 + 3*a^7 + a^6 - 3*a^5 + a^4 + 4*a^3 - 3*a^2 - 2*a + 2,
a^16 - a^15 - 3*a^14 - 4*a^13 - 4*a^12 - 3*a^11 - a^10 + 2*a^9 + 4*a^8 + 5*a^7 + 4*a^6 + 2*a^5 - 2*a^4 - 6*a^3 - 9*a^2 - 9*a - 7,
a^15 + a^14 + 2*a^11 + a^10 - a^9 + a^8 + 2*a^7 - a^5 + 2*a^3 - a^2 - 3*a + 1,
3*a^16 + 3*a^15 + 3*a^14 + 3*a^13 + 3*a^12 + 2*a^11 + 2*a^10 + 2*a^9 + a^8 - a^7 - 2*a^6 - 3*a^5 - 3*a^4 - 4*a^3 - 6*a^2 - 8*a - 8]
The provable and the conjectural results are cached separately (this fixes trac #2504):
sage: K.units(proof=True)
...
PariError: not enough precomputed primes, need primelimit ~ (35)
Return generators for the unit group modulo torsion.
INPUT:
Note
For more functionality see the unit_group() function.
ALGORITHM: Uses PARI’s bnfunit command.
EXAMPLES:
sage: x = QQ['x'].0
sage: A = x^4 - 10*x^3 + 20*5*x^2 - 15*5^2*x + 11*5^3
sage: K = NumberField(A, 'a')
sage: K.units()
[8/275*a^3 - 12/55*a^2 + 15/11*a - 2]
Sage might not be able to provably compute the unit group:
sage: K = NumberField(x^17 + 3, 'a')
sage: K.units(proof=True) # default
...
PariError: not enough precomputed primes, need primelimit ~ (35)
In this case, one can ask for the conjectural unit group (correct if the Generalized Riemann Hypothesis is true):
sage: K.units(proof=False)
[a^9 + a - 1,
a^16 - a^15 + a^14 - a^12 + a^11 - a^10 - a^8 + a^7 - 2*a^6 + a^4 - 3*a^3 + 2*a^2 - 2*a + 1,
2*a^16 - a^14 - a^13 + 3*a^12 - 2*a^10 + a^9 + 3*a^8 - 3*a^6 + 3*a^5 + 3*a^4 - 2*a^3 - 2*a^2 + 3*a + 4,
2*a^16 - 3*a^15 + 3*a^14 - 3*a^13 + 3*a^12 - a^11 + a^9 - 3*a^8 + 4*a^7 - 5*a^6 + 6*a^5 - 4*a^4 + 3*a^3 - 2*a^2 - 2*a + 4,
a^15 - a^12 + a^10 - a^9 - 2*a^8 + 3*a^7 + a^6 - 3*a^5 + a^4 + 4*a^3 - 3*a^2 - 2*a + 2,
a^16 - a^15 - 3*a^14 - 4*a^13 - 4*a^12 - 3*a^11 - a^10 + 2*a^9 + 4*a^8 + 5*a^7 + 4*a^6 + 2*a^5 - 2*a^4 - 6*a^3 - 9*a^2 - 9*a - 7,
a^15 + a^14 + 2*a^11 + a^10 - a^9 + a^8 + 2*a^7 - a^5 + 2*a^3 - a^2 - 3*a + 1,
3*a^16 + 3*a^15 + 3*a^14 + 3*a^13 + 3*a^12 + 2*a^11 + 2*a^10 + 2*a^9 + a^8 - a^7 - 2*a^6 - 3*a^5 - 3*a^4 - 4*a^3 - 6*a^2 - 8*a - 8]
The provable and the conjectural results are cached separately (this fixes trac #2504):
sage: K.units(proof=True)
...
PariError: not enough precomputed primes, need primelimit ~ (35)
Return one, or a list of all, primitive n-th root of unity in this field.
INPUT:
 -th root of unity in this field, or raise a ValueError
exception if there are none. If True, return a list of
all primitive
-th root of unity in this field, or raise a ValueError
exception if there are none. If True, return a list of
all primitive  -th roots of unity in this field
(possibly empty).
-th roots of unity in this field
(possibly empty).Note
To obtain the maximal order of a root of unity in this field, use self.number_of_roots_of_unity().
Note
We do not create the full unit group since that can be expensive, but we do use it if it is already known.
EXAMPLES:
sage: K.<z> = NumberField(x^2 + 3)
sage: K.zeta(1)
1
sage: K.zeta(2)
-1
sage: K.zeta(2, all=True)
[-1]
sage: K.zeta(3)
1/2*z - 1/2
sage: K.zeta(3, all=True)
[1/2*z - 1/2, -1/2*z - 1/2]
sage: K.zeta(4)
...
ValueError: There are no 4th roots of unity in self.
sage: r.<x> = QQ[]
sage: K.<b> = NumberField(x^2+1)
sage: K.zeta(4)
b
sage: K.zeta(4,all=True)
[b, -b]
sage: K.zeta(3)
...
ValueError: There are no 3rd roots of unity in self.
sage: K.zeta(3,all=True)
[]
Compute the first n coefficients of the Dedekind zeta function of this field as a Dirichlet series.
EXAMPLE:
sage: x = QQ['x'].0
sage: NumberField(x^2+1, 'a').zeta_coefficients(10)
[1, 1, 0, 1, 2, 0, 0, 1, 1, 2]
Return the Zeta function of this number field.
This actually returns an interface to Tim Dokchitser’s program for computing with the Dedekind zeta function zeta_F(s) of the number field F.
INPUT:
OUTPUT: The zeta function of this number field.
EXAMPLES:
sage: K.<a> = NumberField(ZZ['x'].0^2+ZZ['x'].0-1)
sage: Z = K.zeta_function()
sage: Z
Zeta function associated to Number Field in a with defining polynomial x^2 + x - 1
sage: Z(-1)
0.0333333333333333
sage: L.<a, b, c> = NumberField([x^2 - 5, x^2 + 3, x^2 + 1])
sage: Z = L.zeta_function()
sage: Z(5)
1.00199015670185
Return the number of roots of unity in this field.
Note
We do not create the full unit group since that can be expensive, but we do use it if it is already known.
EXAMPLES:
sage: F.<alpha> = NumberField(x**22+3)
sage: F.zeta_order()
6
sage: F.<alpha> = NumberField(x**2-7)
sage: F.zeta_order()
2
This is used in pickling generic number fields.
EXAMPLES:
sage: from sage.rings.number_field.number_field import NumberField_generic_v1
sage: R.<x> = QQ[]
sage: NumberField_generic_v1(x^2 + 1, 'i', 'i')
Number Field in i with defining polynomial x^2 + 1
Bases: sage.rings.number_field.number_field.NumberField_absolute
Create a quadratic extension of the rational field.
The command QuadraticField(a) creates the field 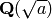 .
.
EXAMPLES:
sage: QuadraticField(3, 'a')
Number Field in a with defining polynomial x^2 - 3
sage: QuadraticField(-4, 'b')
Number Field in b with defining polynomial x^2 + 4
Return the size of the class group of self.
If proof = False (not the default!) and the discriminant of the field is negative, then the following warning from the PARI manual applies:
Warning
For 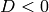 , this function may give incorrect results when
the class group has a low exponent (has many cyclic
factors), because implementing Shank’s method in full
generality slows it down immensely.
, this function may give incorrect results when
the class group has a low exponent (has many cyclic
factors), because implementing Shank’s method in full
generality slows it down immensely.
EXAMPLES:
sage: QuadraticField(-23,'a').class_number()
3
These are all the primes so that the class number of
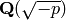 is
is  :
:
sage: [d for d in prime_range(2,300) if not is_square(d) and QuadraticField(-d,'a').class_number() == 1]
[2, 3, 7, 11, 19, 43, 67, 163]
It is an open problem to prove that there are infinity many
positive square-free  such that
such that
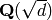 has class number
has class number  :
:
sage: len([d for d in range(2,200) if not is_square(d) and QuadraticField(d,'a').class_number() == 1])
121
TESTS:
sage: type(QuadraticField(-23,'a').class_number())
<type 'sage.rings.integer.Integer'>
sage: type(NumberField(x^3 + 23, 'a').class_number())
<type 'sage.rings.integer.Integer'>
sage: type(NumberField(x^3 + 23, 'a').extension(x^2 + 5, 'b').class_number())
<type 'sage.rings.integer.Integer'>
sage: type(CyclotomicField(10).class_number())
<type 'sage.rings.integer.Integer'>
Returns the discriminant of the ring of integers of the number field, or if v is specified, the determinant of the trace pairing on the elements of the list v.
INPUT:
OUTPUT: Integer if v is omitted, and Rational otherwise.
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: K.discriminant()
-4
sage: K.<a> = NumberField(x^2+5)
sage: K.discriminant()
-20
sage: K.<a> = NumberField(x^2-5)
sage: K.discriminant()
5
Returns the Hilbert class field of this quadratic field as a relative extension of this field.
Note
For the polynomial that defines this field as a relative extension, see the hilbert_class_field_defining_polynomial command, which is vastly faster than this command, since it doesn’t construct a relative extension.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 23)
sage: L = K.hilbert_class_field('b'); L
Number Field in b with defining polynomial x^3 + x^2 - 1 over its base field
sage: L.absolute_field('c')
Number Field in c with defining polynomial x^6 + 2*x^5 + 70*x^4 + 90*x^3 + 1631*x^2 + 1196*x + 12743
sage: K.hilbert_class_field_defining_polynomial()
x^3 + x^2 - 1
Returns a polynomial over  whose roots generate
Hilbert class field of this quadratic field as an extension of
this quadratic field.
whose roots generate
Hilbert class field of this quadratic field as an extension of
this quadratic field.
Note
Computed using PARI via Schertz’s method. This implementation is quite fast.
EXAMPLES:
sage: K.<b> = QuadraticField(-23)
sage: K.hilbert_class_field_defining_polynomial()
x^3 + x^2 - 1
Note that this polynomial is not the actual Hilbert class polynomial: see hilbert_class_polynomial.
sage: K.hilbert_class_polynomial()
x^3 + 3491750*x^2 - 5151296875*x + 12771880859375
sage: K.<a> = QuadraticField(-431)
sage: K.class_number()
21
sage: K.hilbert_class_field_defining_polynomial(name='z')
z^21 + z^20 - 13*z^19 - 50*z^18 + 592*z^17 - 2403*z^16 + 5969*z^15 - 10327*z^14 + 13253*z^13 - 12977*z^12 + 9066*z^11 - 2248*z^10 - 5523*z^9 + 11541*z^8 - 13570*z^7 + 11315*z^6 - 6750*z^5 + 2688*z^4 - 577*z^3 + 9*z^2 + 15*z + 1
Compute the Hilbert class polynomial of this quadratic field.
Right now, this is only implemented for imaginary quadratic fields.
EXAMPLES:
sage: K.<a> = QuadraticField(-3)
sage: K.hilbert_class_polynomial()
x
sage: K.<a> = QuadraticField(-31)
sage: K.hilbert_class_polynomial(name='z')
z^3 + 39491307*z^2 - 58682638134*z + 1566028350940383
Return True since all quadratic fields are automatically Galois.
EXAMPLES:
sage: QuadraticField(1234,'d').is_galois()
True
This is used in pickling quadratic fields.
EXAMPLES:
sage: from sage.rings.number_field.number_field import NumberField_quadratic_v1
sage: R.<x> = QQ[]
sage: NumberField_quadratic_v1(x^2 - 2, 'd')
Number Field in d with defining polynomial x^2 - 2
Return a quadratic field obtained by adjoining a square root of
 to the rational numbers, where
to the rational numbers, where  is not a
perfect square.
is not a
perfect square.
INPUT:
OUTPUT: A number field defined by a quadratic polynomial. Unless
otherwise specified, it has an embedding into  or
or
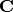 by sending the generator to the positive
or upper-half-plane root.
by sending the generator to the positive
or upper-half-plane root.
EXAMPLES:
sage: QuadraticField(3, 'a')
Number Field in a with defining polynomial x^2 - 3
sage: K.<theta> = QuadraticField(3); K
Number Field in theta with defining polynomial x^2 - 3
sage: RR(theta)
1.73205080756888
sage: QuadraticField(9, 'a')
...
ValueError: D must not be a perfect square.
sage: QuadraticField(9, 'a', check=False)
Number Field in a with defining polynomial x^2 - 9
Quadratic number fields derive from general number fields.
sage: from sage.rings.number_field.number_field import is_NumberField
sage: type(K)
<class 'sage.rings.number_field.number_field.NumberField_quadratic_with_category'>
sage: is_NumberField(K)
True
Quadratic number fields are cached:
sage: QuadraticField(-11, 'a') is QuadraticField(-11, 'a')
True
By default, quadratic fields come with a nice latex representation:
sage: K.<a> = QuadraticField(-7)
sage: latex(a)
\sqrt{-7}
sage: latex(1/(1+a))
-\frac{1}{8} \sqrt{-7} + \frac{1}{8}
sage: K.latex_variable_name()
'\\sqrt{-7}'
We can provide our own name as well:
sage: K.<a> = QuadraticField(next_prime(10^10), latex_name=r'\sqrt{D}')
sage: 1+a
a + 1
sage: latex(1+a)
\sqrt{D} + 1
sage: latex(QuadraticField(-1, 'a', latex_name=None).gen())
a
TESTS:
sage: QuadraticField(-11, 'a') is QuadraticField(-11, 'a', latex_name='Z')
False
sage: QuadraticField(-11, 'a') is QuadraticField(-11, 'a', latex_name=None)
False
Return the unique copy of the gp (PARI) interpreter used for number field computations.
EXAMPLES:
sage: from sage.rings.number_field.number_field import gp
sage: gp()
GP/PARI interpreter
Return True if x is an absolute number field.
EXAMPLES:
sage: from sage.rings.number_field.number_field import is_AbsoluteNumberField
sage: is_AbsoluteNumberField(NumberField(x^2+1,'a'))
True
sage: is_AbsoluteNumberField(NumberField([x^3 + 17, x^2+1],'a'))
False
The rationals are a number field, but they’re not of the absolute number field class.
sage: is_AbsoluteNumberField(QQ)
False
Return True if x is a cyclotomic field, i.e., of the special cyclotomic field class. This function does not return True for a number field that just happens to be isomorphic to a cyclotomic field.
EXAMPLES:
sage: from sage.rings.number_field.number_field import is_CyclotomicField
sage: is_CyclotomicField(NumberField(x^2 + 1,'zeta4'))
False
sage: is_CyclotomicField(CyclotomicField(4))
True
sage: is_CyclotomicField(CyclotomicField(1))
True
sage: is_CyclotomicField(QQ)
False
sage: is_CyclotomicField(7)
False
Returns whether codomain is a valid codomain for a number field homset. This is used by NumberField._Hom_ to determine whether the created homsets should be a sage.rings.number_field.morphism.NumberFieldHomset.
EXAMPLES:
This currently accepts any parent (CC, RR, ...) in Fields:
sage: from sage.rings.number_field.number_field import is_NumberFieldHomsetCodomain
sage: is_NumberFieldHomsetCodomain(QQ)
True
sage: is_NumberFieldHomsetCodomain(NumberField(x^2 + 1, 'x'))
True
sage: is_NumberFieldHomsetCodomain(ZZ)
False
sage: is_NumberFieldHomsetCodomain(3)
False
sage: is_NumberFieldHomsetCodomain(MatrixSpace(QQ, 2))
False
sage: is_NumberFieldHomsetCodomain(InfinityRing)
False
Question: should, for example, QQ-algebras be accepted as well?
Caveat: Gap objects are not (yet) in Fields, and therefore not accepted as number field homset codomains:
sage: is_NumberFieldHomsetCodomain(gap.Rationals)
False
Return True if x is of the quadratic number field type.
EXAMPLES:
sage: from sage.rings.number_field.number_field import is_QuadraticField
sage: is_QuadraticField(QuadraticField(5,'a'))
True
sage: is_QuadraticField(NumberField(x^2 - 5, 'b'))
True
sage: is_QuadraticField(NumberField(x^3 - 5, 'b'))
False
A quadratic field specially refers to a number field, not a finite field:
sage: is_QuadraticField(GF(9,'a'))
False
Return True if the integer  is a fundamental
discriminant, i.e., if
is a fundamental
discriminant, i.e., if 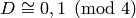 , and
, and
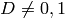 and either (1)
and either (1)  is square free or
(2) we have
is square free or
(2) we have 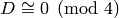 with
with
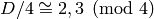 and
and  square free. These
are exactly the discriminants of quadratic fields.
square free. These
are exactly the discriminants of quadratic fields.
EXAMPLES:
sage: [D for D in range(-15,15) if is_fundamental_discriminant(D)]
[-15, -11, -8, -7, -4, -3, 5, 8, 12, 13]
sage: [D for D in range(-15,15) if not is_square(D) and QuadraticField(D,'a').disc() == D]
[-15, -11, -8, -7, -4, -3, 5, 8, 12, 13]
Used for easily determining the correct proof flag to use.
Returns t if t is not None, otherwise returns the system-wide proof-flag for number fields (default: True).
EXAMPLES:
sage: from sage.rings.number_field.number_field import proof_flag
sage: proof_flag(True)
True
sage: proof_flag(False)
False
sage: proof_flag(None)
True
sage: proof_flag("banana")
'banana'
Helper function for embeddings() functions for number fields.
INPUT: a list of embeddings of a number field
OUTPUT: None. The list is altered in-place, so that, if possible, the first embedding has been switched with one of the others, so that if there is an embedding which preserves the generator names then it appears first.
EXAMPLES:
sage: K.<a> = CyclotomicField(7)
sage: embs = K.embeddings(K)
sage: [e(a) for e in embs] # random - there is no natural sort order
[a, a^2, a^3, a^4, a^5, -a^5 - a^4 - a^3 - a^2 - a - 1]
sage: id = [ e for e in embs if e(a) == a ][0]; id
Ring endomorphism of Cyclotomic Field of order 7 and degree 6
Defn: a |--> a
sage: permuted_embs = list(embs); permuted_embs.remove(id); permuted_embs.append(id)
sage: [e(a) for e in permuted_embs] # random - but natural map is not first
[a^2, a^3, a^4, a^5, -a^5 - a^4 - a^3 - a^2 - a - 1, a]
sage: permuted_embs[0] != a
True
sage: from sage.rings.number_field.number_field import put_natural_embedding_first
sage: put_natural_embedding_first(permuted_embs)
sage: [e(a) for e in permuted_embs] # random - but natural map is first
[a, a^3, a^4, a^5, -a^5 - a^4 - a^3 - a^2 - a - 1, a^2]
sage: permuted_embs[0] == id
True
Given an embedding from a number field to either  or
or
 , returns an equivalent embedding with higher precision.
, returns an equivalent embedding with higher precision.
INPUT:
e - an embedding of a number field into either RR or CC (with some precision)
current precision is doubled; if Infinity, the equivalent embedding into either QQbar or AA is returned.
EXAMPLES:
sage: from sage.rings.number_field.number_field import refine_embedding
sage: K = CyclotomicField(3)
sage: e10 = K.complex_embedding(10)
sage: e10.codomain().precision()
10
sage: e25 = refine_embedding(e10, prec=25)
sage: e25.codomain().precision()
25
An example where we extend a real embedding into AA:
sage: K.<a> = NumberField(x^3-2)
sage: K.signature()
(1, 1)
sage: e = K.embeddings(RR)[0]; e
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Real Field with 53 bits of precision
Defn: a |--> 1.25992104989487
sage: e = refine_embedding(e,Infinity); e
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Algebraic Real Field
Defn: a |--> 1.259921049894873?
Now we can obtain arbitrary precision values with no trouble:
sage: RealField(150)(e(a))
1.2599210498948731647672106072782283505702515
sage: _^3
2.0000000000000000000000000000000000000000000
sage: RealField(200)(e(a^2-3*a+7))
4.8076379022835799804500738174376232086807389337953290695624
Complex embeddings can be extended into QQbar:
sage: e = K.embeddings(CC)[0]; e
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Complex Field with 53 bits of precision
Defn: a |--> -0.62996052494743... - 1.09112363597172*I
sage: e = refine_embedding(e,Infinity); e
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Algebraic Field
Defn: a |--> -0.6299605249474365? - 1.091123635971722?*I
sage: ComplexField(200)(e(a))
-0.62996052494743658238360530363911417528512573235075399004099 - 1.0911236359717214035600726141898088813258733387403009407036*I
sage: e(a)^3
2
Embeddings into lazy fields work:
sage: L = CyclotomicField(7)
sage: x = L.specified_complex_embedding(); x
Generic morphism:
From: Cyclotomic Field of order 7 and degree 6
To: Complex Lazy Field
Defn: zeta7 -> 0.623489801858734? + 0.781831482468030?*I
sage: refine_embedding(x, 300)
Ring morphism:
From: Cyclotomic Field of order 7 and degree 6
To: Complex Field with 300 bits of precision
Defn: zeta7 |--> 0.623489801858733530525004884004239810632274730896402105365549439096853652456487284575942507 + 0.781831482468029808708444526674057750232334518708687528980634958045091731633936441700868007*I
sage: refine_embedding(x, infinity)
Ring morphism:
From: Cyclotomic Field of order 7 and degree 6
To: Algebraic Field
Defn: zeta7 |--> 0.6234898018587335? + 0.7818314824680299?*I