Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Miscellaneous »
Returns a solution to a Chinese Remainder Theorem problem.
INPUT:
OUTPUT:
If m, n are not None, returns a solution  to the
simultaneous congruences
to the
simultaneous congruences 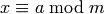 and
and 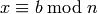 , if one exists. By the Chinese Remainder Theorem, a solution to the
simultaneous congruences exists if and only if
, if one exists. By the Chinese Remainder Theorem, a solution to the
simultaneous congruences exists if and only if
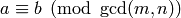 . The solution
. The solution  is only well-defined modulo
is only well-defined modulo
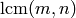 .
.
If a and b are lists, returns a simultaneous solution to
the congruences 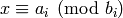 , if one exists.
, if one exists.
See also
EXAMPLES:
Using crt by giving it pairs of residues and moduli:
sage: crt(2, 1, 3, 5)
11
sage: crt(13, 20, 100, 301)
28013
sage: crt([2, 1], [3, 5])
11
sage: crt([13, 20], [100, 301])
28013
You can also use upper case:
sage: c = CRT(2,3, 3, 5); c
8
sage: c % 3 == 2
True
sage: c % 5 == 3
True
Note that this also works for polynomial rings:
sage: K.<a> = NumberField(x^3 - 7)
sage: R.<y> = K[]
sage: f = y^2 + 3
sage: g = y^3 - 5
sage: CRT(1,3,f,g)
-3/26*y^4 + 5/26*y^3 + 15/26*y + 53/26
sage: CRT(1,a,f,g)
(-3/52*a + 3/52)*y^4 + (5/52*a - 5/52)*y^3 + (15/52*a - 15/52)*y + 27/52*a + 25/52
You can also do this for any number of moduli:
sage: K.<a> = NumberField(x^3 - 7)
sage: R.<x> = K[]
sage: CRT([], [])
0
sage: CRT([a], [x])
a
sage: f = x^2 + 3
sage: g = x^3 - 5
sage: h = x^5 + x^2 - 9
sage: k = CRT([1, a, 3], [f, g, h]); k
(127/26988*a - 5807/386828)*x^9 + (45/8996*a - 33677/1160484)*x^8 + (2/173*a - 6/173)*x^7 + (133/6747*a - 5373/96707)*x^6 + (-6/2249*a + 18584/290121)*x^5 + (-277/8996*a + 38847/386828)*x^4 + (-135/4498*a + 42673/193414)*x^3 + (-1005/8996*a + 470245/1160484)*x^2 + (-1215/8996*a + 141165/386828)*x + 621/8996*a + 836445/386828
sage: k.mod(f)
1
sage: k.mod(g)
a
sage: k.mod(h)
3
If the moduli are not coprime, a solution may not exist:
sage: crt(4,8,8,12)
20
sage: crt(4,6,8,12)
...
ValueError: No solution to crt problem since gcd(8,12) does not divide 4-6
sage: x = polygen(QQ)
sage: crt(2,3,x-1,x+1)
-1/2*x + 5/2
sage: crt(2,x,x^2-1,x^2+1)
-1/2*x^3 + x^2 + 1/2*x + 1
sage: crt(2,x,x^2-1,x^3-1)
...
ValueError: No solution to crt problem since gcd(x^2 - 1,x^3 - 1) does not divide 2-x
Returns a CRT basis for the given moduli.
INPUT:
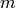 which admit an
which admit anextended Euclidean algorithm
OUTPUT:
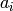 of the same length as
of the same length as 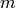 such that
such that
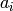 is congruent to 1 modulo
is congruent to 1 modulo 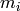 and to 0 modulo
and to 0 modulo 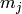 for
for
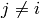 .
.Note
The pairwise coprimality of the input is not checked.
EXAMPLES:
sage: a1 = ZZ(mod(42,5))
sage: a2 = ZZ(mod(42,13))
sage: c1,c2 = CRT_basis([5,13])
sage: mod(a1*c1+a2*c2,5*13)
42
A polynomial example:
sage: x=polygen(QQ)
sage: mods = [x,x^2+1,2*x-3]
sage: b = CRT_basis(mods)
sage: b
[-2/3*x^3 + x^2 - 2/3*x + 1, 6/13*x^3 - x^2 + 6/13*x, 8/39*x^3 + 8/39*x]
sage: [[bi % mj for mj in mods] for bi in b]
[[1, 0, 0], [0, 1, 0], [0, 0, 1]]
Given a list v of elements and a list of corresponding moduli, find a single element that reduces to each element of v modulo the corresponding moduli.
See also
EXAMPLES:
sage: CRT_list([2,3,2], [3,5,7])
23
sage: x = polygen(QQ)
sage: c = CRT_list([3], [x]); c
3
sage: c.parent()
Univariate Polynomial Ring in x over Rational Field
The arguments must be lists:
sage: CRT_list([1,2,3],"not a list")
...
ValueError: Arguments to CRT_list should be lists
sage: CRT_list("not a list",[2,3])
...
ValueError: Arguments to CRT_list should be lists
The list of moduli must have the same length as the list of elements:
sage: CRT_list([1,2,3],[2,3,5])
23
sage: CRT_list([1,2,3],[2,3])
...
ValueError: Arguments to CRT_list should be lists of the same length
sage: CRT_list([1,2,3],[2,3,5,7])
...
ValueError: Arguments to CRT_list should be lists of the same length
Vector form of the Chinese Remainder Theorem: given a list of integer
vectors 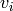 and a list of coprime moduli
and a list of coprime moduli 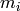 , find a vector
, find a vector 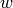 such
that
such
that 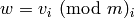 for all
for all  . This is more efficient than applying
CRT() to each entry.
. This is more efficient than applying
CRT() to each entry.
INPUT:
OUTPUT:
EXAMPLES:
sage: CRT_vectors([[3,5,7],[3,5,11]], [2,3])
[3, 5, 5]
sage: CRT_vectors([vector(ZZ, [2,3,1]), Sequence([1,7,8],ZZ)], [8,9])
[10, 43, 17]
Return the value of the Euler phi function on the integer n. We defined this to be the number of positive integers <= n that are relatively prime to n. Thus if n<=0 then euler_phi(n) is defined and equals 0.
INPUT:
EXAMPLES:
sage: euler_phi(1)
1
sage: euler_phi(2)
1
sage: euler_phi(3)
2
sage: euler_phi(12)
4
sage: euler_phi(37)
36
Notice that euler_phi is defined to be 0 on negative numbers and 0.
sage: euler_phi(-1)
0
sage: euler_phi(0)
0
sage: type(euler_phi(0))
<type 'sage.rings.integer.Integer'>
We verify directly that the phi function is correct for 21.
sage: euler_phi(21)
12
sage: [i for i in range(21) if gcd(21,i) == 1]
[1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20]
The length of the list of integers ‘i’ in range(n) such that the gcd(i,n) == 1 equals euler_phi(n).
sage: len([i for i in range(21) if gcd(21,i) == 1]) == euler_phi(21)
True
The phi function also has a special plotting method.
sage: P = plot(euler_phi, -3, 71)
AUTHORS:
Plot the Euler phi function.
INPUT:
EXAMPLES:
sage: p = Euler_Phi().plot()
sage: p.ymax()
46.0
The greatest common divisor of a and b, or if a is a list and b is omitted the greatest common divisor of all elements of a.
INPUT:
Additional keyword arguments are passed to the respectively called methods.
EXAMPLES:
sage: GCD(97,100)
1
sage: GCD(97*10^15, 19^20*97^2)
97
sage: GCD(2/3, 4/3)
1
sage: GCD([2,4,6,8])
2
sage: GCD(srange(0,10000,10)) # fast !!
10
Note that to take the gcd of  elements for
elements for 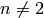 you must
put the elements into a list by enclosing them in [..]. Before
#4988 the following wrongly returned 3 since the third parameter
was just ignored:
you must
put the elements into a list by enclosing them in [..]. Before
#4988 the following wrongly returned 3 since the third parameter
was just ignored:
sage: gcd(3,6,2)
...
TypeError: gcd() takes at most 2 arguments (3 given)
sage: gcd([3,6,2])
1
Similarly, giving just one element (which is not a list) gives an error:
sage: gcd(3)
...
TypeError: 'sage.rings.integer.Integer' object is not iterable
By convention, the gcd of the empty list is (the integer) 0:
sage: gcd([])
0
sage: type(gcd([]))
<type 'sage.rings.integer.Integer'>
The least common multiple of a and b, or if a is a list and b is omitted the least common multiple of all elements of a.
Note that LCM is an alias for lcm.
INPUT:
EXAMPLES:
sage: lcm(97,100)
9700
sage: LCM(97,100)
9700
sage: LCM(0,2)
0
sage: LCM(-3,-5)
15
sage: LCM([1,2,3,4,5])
60
sage: v = LCM(range(1,10000)) # *very* fast!
sage: len(str(v))
4349
Returns the value of the Moebius function of abs(n), where n is an integer.
DEFINITION:  is 0 if
is 0 if  is not square
free, and otherwise equals
is not square
free, and otherwise equals 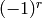 , where
, where  has
has
 distinct prime factors.
distinct prime factors.
For simplicity, if  we define
we define 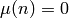 .
.
IMPLEMENTATION: Factors or - for integers - uses the PARI C library.
INPUT:
OUTPUT: 0, 1, or -1
EXAMPLES:
sage: moebius(-5)
-1
sage: moebius(9)
0
sage: moebius(12)
0
sage: moebius(-35)
1
sage: moebius(-1)
1
sage: moebius(7)
-1
sage: moebius(0) # potentially nonstandard!
0
The moebius function even makes sense for non-integer inputs.
sage: x = GF(7)['x'].0
sage: moebius(x+2)
-1
Plot the Moebius function.
INPUT:
EXAMPLES:
sage: p = Moebius().plot()
sage: p.ymax()
1.0
Return the Moebius function evaluated at the given range of values, i.e., the image of the list range(start, stop, step) under the Mobius function.
This is much faster than directly computing all these values with a list comprehension.
EXAMPLES:
sage: v = moebius.range(-10,10); v
[1, 0, 0, -1, 1, -1, 0, -1, -1, 1, 0, 1, -1, -1, 0, -1, 1, -1, 0, 0]
sage: v == [moebius(n) for n in range(-10,10)]
True
sage: v = moebius.range(-1000, 2000, 4)
sage: v == [moebius(n) for n in range(-1000,2000, 4)]
True
Return the sum of the k-th powers of the divisors of n.
INPUT:
OUTPUT: integer
EXAMPLES:
sage: sigma(5)
6
sage: sigma(5,2)
26
The sigma function also has a special plotting method.
sage: P = plot(sigma, 1, 100)
This method also works with k-th powers.
sage: P = plot(sigma, 1, 100, k=2)
AUTHORS:
TESTS:
sage: sigma(100,4)
106811523
sage: sigma(factorial(100),3).mod(144169)
3672
sage: sigma(factorial(150),12).mod(691)
176
sage: RR(sigma(factorial(133),20))
2.80414775675747e4523
sage: sigma(factorial(100),0)
39001250856960000
sage: sigma(factorial(41),1)
229199532273029988767733858700732906511758707916800
Plot the sigma (sum of k-th powers of divisors) function.
INPUT:
EXAMPLES:
sage: p = Sigma().plot()
sage: p.ymax()
124.0
Return a triple (g,s,t) such that 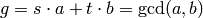 .
.
Note
One exception is if  and
and 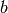 are not in a PID, e.g., they are
both polynomials over the integers, then this function can’t in
general return (g,s,t) as above, since they need not exist.
Instead, over the integers, we first multiply
are not in a PID, e.g., they are
both polynomials over the integers, then this function can’t in
general return (g,s,t) as above, since they need not exist.
Instead, over the integers, we first multiply 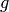 by a divisor of
the resultant of
by a divisor of
the resultant of 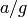 and
and  , up to sign.
, up to sign.
INPUT:
OUTPUT:

Note
There is no guarantee that the returned cofactors (s and t) are minimal. In the integer case, see sage.rings.integer.Integer._xgcd() for minimal cofactors.
EXAMPLES:
sage: xgcd(56, 44)
(4, 4, -5)
sage: 4*56 + (-5)*44
4
sage: g, a, b = xgcd(5/1, 7/1); g, a, b
(1, 3, -2)
sage: a*(5/1) + b*(7/1) == g
True
sage: x = polygen(QQ)
sage: xgcd(x^3 - 1, x^2 - 1)
(x - 1, 1, -x)
sage: K.<g> = NumberField(x^2-3)
sage: R.<a,b> = K[]
sage: S.<y> = R.fraction_field()[]
sage: xgcd(y^2, a*y+b)
(1, a^2/b^2, ((-a)/b^2)*y + 1/b)
sage: xgcd((b+g)*y^2, (a+g)*y+b)
(1, (a^2 + (2*g)*a + 3)/(b^3 + (g)*b^2), ((-a + (-g))/b^2)*y + 1/b)
We compute an xgcd over the integers, where the linear combination is not the gcd but the resultant:
sage: R.<x> = ZZ[]
sage: gcd(2*x*(x-1), x^2)
x
sage: xgcd(2*x*(x-1), x^2)
(2*x, -1, 2)
sage: (2*(x-1)).resultant(x)
2
Returns a polynomial of degree at most 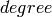 which is
approximately satisfied by the number
which is
approximately satisfied by the number  . Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if
. Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if  is a good approximation to an algebraic
number of degree less than
is a good approximation to an algebraic
number of degree less than 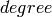 .
.
You can specify the number of known bits or digits with known_bits=k or
known_digits=k; Pari is then told to compute the result using 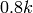 of these bits/digits. (The Pari documentation recommends using a factor
between .6 and .9, but internally defaults to .8.) Or, you can specify the
precision to use directly with use_bits=k or use_digits=k. If none
of these are specified, then the precision is taken from the input value.
of these bits/digits. (The Pari documentation recommends using a factor
between .6 and .9, but internally defaults to .8.) Or, you can specify the
precision to use directly with use_bits=k or use_digits=k. If none
of these are specified, then the precision is taken from the input value.
A height bound may specified to indicate the maximum coefficient size of the returned polynomial; if a sufficiently small polyomial is not found then None wil be returned. If proof=True then the result is returned only if it can be proved correct (i.e. the only possible minimal polynomial satisfying the height bound, or no such polynomial exists). Otherwise a ValueError is raised indicating that higher precision is required.
ALGORITHM: Uses LLL for real/complex inputs, PARI C-library algdep command otherwise.
Note that algebraic_dependency is a synonym for algdep.
INPUT:
z - real, complex, or  -adic number
-adic number
degree - an integer
coefficient size for the returned polynomial
proof - a boolean (default False), requres height_bound to be set
EXAMPLES:
sage: algdep(1.888888888888888, 1)
9*x - 17
sage: algdep(0.12121212121212,1)
33*x - 4
sage: algdep(sqrt(2),2)
x^2 - 2
This example involves a complex number.
sage: z = (1/2)*(1 + RDF(sqrt(3)) *CC.0); z
0.500000000000000 + 0.866025403784439*I
sage: p = algdep(z, 6); p
x^3 + 1
sage: p.factor()
(x + 1) * (x^2 - x + 1)
sage: z^2 - z + 1
0
This example involves a  -adic number.
-adic number.
sage: K = Qp(3, print_mode = 'series')
sage: a = K(7/19); a
1 + 2*3 + 3^2 + 3^3 + 2*3^4 + 2*3^5 + 3^8 + 2*3^9 + 3^11 + 3^12 + 2*3^15 + 2*3^16 + 3^17 + 2*3^19 + O(3^20)
sage: algdep(a, 1)
19*x - 7
These examples show the importance of proper precision control. We compute a 200-bit approximation to sqrt(2) which is wrong in the 33’rd bit.
sage: z = sqrt(RealField(200)(2)) + (1/2)^33
sage: p = algdep(z, 4); p
227004321085*x^4 - 216947902586*x^3 - 99411220986*x^2 + 82234881648*x - 211871195088
sage: factor(p)
227004321085*x^4 - 216947902586*x^3 - 99411220986*x^2 + 82234881648*x - 211871195088
sage: algdep(z, 4, known_bits=32)
x^2 - 2
sage: algdep(z, 4, known_digits=10)
x^2 - 2
sage: algdep(z, 4, use_bits=25)
x^2 - 2
sage: algdep(z, 4, use_digits=8)
x^2 - 2
Using the height_bound and proof parameters, we can see that
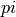 is not the root of an integer polynomial of degree at most 5
and coefficients bounded above by 10.
is not the root of an integer polynomial of degree at most 5
and coefficients bounded above by 10.
sage: algdep(pi.n(), 5, height_bound=10, proof=True) is None
True
For stronger results, we need more precicion.
sage: algdep(pi.n(), 5, height_bound=100, proof=True) is None
...
ValueError: insufficient precision for non-existence proof
sage: algdep(pi.n(200), 5, height_bound=100, proof=True) is None
True
sage: algdep(pi.n(), 10, height_bound=10, proof=True) is None
...
ValueError: insufficient precision for non-existence proof
sage: algdep(pi.n(200), 10, height_bound=10, proof=True) is None
True
We can also use proof=True to get positive results.
sage: a = sqrt(2) + sqrt(3) + sqrt(5)
sage: algdep(a.n(), 8, height_bound=1000, proof=True)
...
ValueError: insufficient precision for uniqueness proof
sage: f = algdep(a.n(1000), 8, height_bound=1000, proof=True); f
x^8 - 40*x^6 + 352*x^4 - 960*x^2 + 576
sage: f(a).expand()
0
Returns a polynomial of degree at most 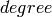 which is
approximately satisfied by the number
which is
approximately satisfied by the number  . Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if
. Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if  is a good approximation to an algebraic
number of degree less than
is a good approximation to an algebraic
number of degree less than 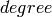 .
.
You can specify the number of known bits or digits with known_bits=k or
known_digits=k; Pari is then told to compute the result using 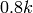 of these bits/digits. (The Pari documentation recommends using a factor
between .6 and .9, but internally defaults to .8.) Or, you can specify the
precision to use directly with use_bits=k or use_digits=k. If none
of these are specified, then the precision is taken from the input value.
of these bits/digits. (The Pari documentation recommends using a factor
between .6 and .9, but internally defaults to .8.) Or, you can specify the
precision to use directly with use_bits=k or use_digits=k. If none
of these are specified, then the precision is taken from the input value.
A height bound may specified to indicate the maximum coefficient size of the returned polynomial; if a sufficiently small polyomial is not found then None wil be returned. If proof=True then the result is returned only if it can be proved correct (i.e. the only possible minimal polynomial satisfying the height bound, or no such polynomial exists). Otherwise a ValueError is raised indicating that higher precision is required.
ALGORITHM: Uses LLL for real/complex inputs, PARI C-library algdep command otherwise.
Note that algebraic_dependency is a synonym for algdep.
INPUT:
z - real, complex, or  -adic number
-adic number
degree - an integer
coefficient size for the returned polynomial
proof - a boolean (default False), requres height_bound to be set
EXAMPLES:
sage: algdep(1.888888888888888, 1)
9*x - 17
sage: algdep(0.12121212121212,1)
33*x - 4
sage: algdep(sqrt(2),2)
x^2 - 2
This example involves a complex number.
sage: z = (1/2)*(1 + RDF(sqrt(3)) *CC.0); z
0.500000000000000 + 0.866025403784439*I
sage: p = algdep(z, 6); p
x^3 + 1
sage: p.factor()
(x + 1) * (x^2 - x + 1)
sage: z^2 - z + 1
0
This example involves a  -adic number.
-adic number.
sage: K = Qp(3, print_mode = 'series')
sage: a = K(7/19); a
1 + 2*3 + 3^2 + 3^3 + 2*3^4 + 2*3^5 + 3^8 + 2*3^9 + 3^11 + 3^12 + 2*3^15 + 2*3^16 + 3^17 + 2*3^19 + O(3^20)
sage: algdep(a, 1)
19*x - 7
These examples show the importance of proper precision control. We compute a 200-bit approximation to sqrt(2) which is wrong in the 33’rd bit.
sage: z = sqrt(RealField(200)(2)) + (1/2)^33
sage: p = algdep(z, 4); p
227004321085*x^4 - 216947902586*x^3 - 99411220986*x^2 + 82234881648*x - 211871195088
sage: factor(p)
227004321085*x^4 - 216947902586*x^3 - 99411220986*x^2 + 82234881648*x - 211871195088
sage: algdep(z, 4, known_bits=32)
x^2 - 2
sage: algdep(z, 4, known_digits=10)
x^2 - 2
sage: algdep(z, 4, use_bits=25)
x^2 - 2
sage: algdep(z, 4, use_digits=8)
x^2 - 2
Using the height_bound and proof parameters, we can see that
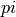 is not the root of an integer polynomial of degree at most 5
and coefficients bounded above by 10.
is not the root of an integer polynomial of degree at most 5
and coefficients bounded above by 10.
sage: algdep(pi.n(), 5, height_bound=10, proof=True) is None
True
For stronger results, we need more precicion.
sage: algdep(pi.n(), 5, height_bound=100, proof=True) is None
...
ValueError: insufficient precision for non-existence proof
sage: algdep(pi.n(200), 5, height_bound=100, proof=True) is None
True
sage: algdep(pi.n(), 10, height_bound=10, proof=True) is None
...
ValueError: insufficient precision for non-existence proof
sage: algdep(pi.n(200), 10, height_bound=10, proof=True) is None
True
We can also use proof=True to get positive results.
sage: a = sqrt(2) + sqrt(3) + sqrt(5)
sage: algdep(a.n(), 8, height_bound=1000, proof=True)
...
ValueError: insufficient precision for uniqueness proof
sage: f = algdep(a.n(1000), 8, height_bound=1000, proof=True); f
x^8 - 40*x^6 + 352*x^4 - 960*x^2 + 576
sage: f(a).expand()
0
Return the n-th Bernoulli number, as a rational number.
INPUT:
EXAMPLES:
sage: bernoulli(12)
-691/2730
sage: bernoulli(50)
495057205241079648212477525/66
We demonstrate each of the alternative algorithms:
sage: bernoulli(12, algorithm='gap')
-691/2730
sage: bernoulli(12, algorithm='gp')
-691/2730
sage: bernoulli(12, algorithm='magma') # optional - magma
-691/2730
sage: bernoulli(12, algorithm='pari')
-691/2730
sage: bernoulli(12, algorithm='bernmm')
-691/2730
sage: bernoulli(12, algorithm='bernmm', num_threads=4)
-691/2730
TESTS:
sage: algs = ['gap','gp','pari','bernmm']
sage: test_list = [ZZ.random_element(2, 2255) for _ in range(500)]
sage: vals = [[bernoulli(i,algorithm = j) for j in algs] for i in test_list] #long time (19s)
sage: union([len(union(x))==1 for x in vals]) #long time (depends on previous line)
[True]
sage: algs = ['gp','pari','bernmm']
sage: test_list = [ZZ.random_element(2256, 5000) for _ in range(500)]
sage: vals = [[bernoulli(i,algorithm = j) for j in algs] for i in test_list] #long time (21s)
sage: union([len(union(x))==1 for x in vals]) #long time (depends on previous line)
[True]
AUTHOR:
Return the binomial coefficient
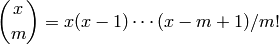
which is defined for 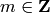 and any
and any
 . We extend this definition to include cases when
. We extend this definition to include cases when
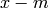 is an integer but
is an integer but 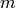 is not by
is not by
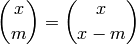
If 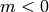 , return
, return 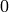 .
.
INPUT:
OUTPUT: number or symbolic expression (if input is symbolic)
EXAMPLES:
sage: binomial(5,2)
10
sage: binomial(2,0)
1
sage: binomial(1/2, 0)
1
sage: binomial(3,-1)
0
sage: binomial(20,10)
184756
sage: binomial(-2, 5)
-6
sage: binomial(RealField()('2.5'), 2)
1.87500000000000
sage: n=var('n'); binomial(n,2)
1/2*(n - 1)*n
sage: n=var('n'); binomial(n,n)
1
sage: n=var('n'); binomial(n,n-1)
n
sage: binomial(2^100, 2^100)
1
sage: k, i = var('k,i')
sage: binomial(k,i)
binomial(k, i)
TESTS:
We test that certain binomials are very fast (this should be instant) – see trac 3309:
sage: a = binomial(RR(1140000.78), 42000000)
We test conversion of arguments to Integers – see trac 6870:
sage: binomial(1/2,1/1)
1/2
sage: binomial(10^20+1/1,10^20)
100000000000000000001
sage: binomial(SR(10**7),10**7)
1
sage: binomial(3/2,SR(1/1))
3/2
Some floating point cases – see trac 7562:
sage: binomial(1.,3)
0.000000000000000
sage: binomial(-2.,3)
-4.00000000000000
Return a dictionary containing pairs
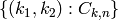 where
where 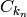 are
binomial coefficients and
are
binomial coefficients and  .
.
INPUT:
OUTPUT: dict
EXAMPLES:
sage: sorted(binomial_coefficients(3).items())
[((0, 3), 1), ((1, 2), 3), ((2, 1), 3), ((3, 0), 1)]
Notice the coefficients above are the same as below:
sage: R.<x,y> = QQ[]
sage: (x+y)^3
x^3 + 3*x^2*y + 3*x*y^2 + y^3
AUTHORS:
Function returns the continuant of the sequence  (list
or tuple).
(list
or tuple).
Definition: see Graham, Knuth and Patashnik, Concrete Mathematics, section 6.7: Continuants. The continuant is defined by
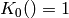
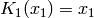
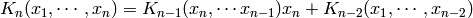
If n = None or n > len(v) the default n = len(v) is used.
INPUT:
OUTPUT: element of ring (integer, polynomial, etcetera).
EXAMPLES:
sage: continuant([1,2,3])
10
sage: p = continuant([2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10])
sage: q = continuant([1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10])
sage: p/q
517656/190435
sage: convergent([2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10],14)
517656/190435
sage: x = PolynomialRing(RationalField(),'x',5).gens()
sage: continuant(x)
x0*x1*x2*x3*x4 + x0*x1*x2 + x0*x1*x4 + x0*x3*x4 + x2*x3*x4 + x0 + x2 + x4
sage: continuant(x, 3)
x0*x1*x2 + x0 + x2
sage: continuant(x,2)
x0*x1 + 1
We verify the identity
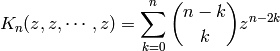
for  using polynomial arithmetic:
using polynomial arithmetic:
sage: z = QQ['z'].0
sage: continuant((z,z,z,z,z,z,z,z,z,z,z,z,z,z,z),6)
z^6 + 5*z^4 + 6*z^2 + 1
sage: continuant(9)
...
TypeError: object of type 'sage.rings.integer.Integer' has no len()
AUTHORS:
Returns the continued fraction of x as a list.
Note
This may be slow for real number input, since it’s implemented in pure Python. For rational number input the PARI C library is used.
EXAMPLES:
sage: continued_fraction_list(45/17)
[2, 1, 1, 1, 5]
sage: continued_fraction_list(e, bits=20)
[2, 1, 2, 1, 1, 4, 1, 1, 6]
sage: continued_fraction_list(e, bits=30)
[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1]
sage: continued_fraction_list(sqrt(2))
[1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1]
sage: continued_fraction_list(sqrt(4/19))
[0, 2, 5, 1, 1, 2, 1, 16, 1, 2, 1, 1, 5, 4, 5, 1, 1, 2, 1, 15, 2]
sage: continued_fraction_list(RR(pi), partial_convergents=True)
([3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 3],
[(3, 1),
(22, 7),
(333, 106),
(355, 113),
(103993, 33102),
(104348, 33215),
(208341, 66317),
(312689, 99532),
(833719, 265381),
(1146408, 364913),
(4272943, 1360120),
(5419351, 1725033),
(80143857, 25510582),
(245850922, 78256779)])
sage: continued_fraction_list(e)
[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 11]
sage: continued_fraction_list(RR(e))
[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 11]
sage: continued_fraction_list(RealField(200)(e))
[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, 1, 16, 1, 1, 18, 1, 1, 20, 1, 1, 22, 1, 1, 24, 1, 1, 26, 1, 1, 28, 1, 1, 30, 1, 1, 32, 1, 1, 34, 1, 1, 36, 1, 1, 38, 1, 1]
Return the n-th continued fraction convergent of the continued
fraction defined by the sequence of integers v. We assume
 .
.
INPUT:
OUTPUT: a rational number
If the continued fraction integers are
![v = [a_0, a_1, a_2, \ldots, a_k]](../../_images/math/e474b371a742dc54e8160b2ab23d521fff227412.png)
then convergent(v,2) is the rational number
and convergent(v,k) is the rational number
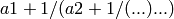
represented by the continued fraction.
EXAMPLES:
sage: convergent([2, 1, 2, 1, 1, 4, 1, 1], 7)
193/71
Return all the partial convergents of a continued fraction defined by the sequence of integers v.
If v is not a list, compute the continued fraction of v and return its convergents (this is potentially much faster than calling continued_fraction first, since continued fractions are implemented using PARI and there is overhead moving the answer back from PARI).
INPUT:
OUTPUT:
EXAMPLES:
sage: convergents([2, 1, 2, 1, 1, 4, 1, 1])
[2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71]
Returns a solution to a Chinese Remainder Theorem problem.
INPUT:
OUTPUT:
If m, n are not None, returns a solution  to the
simultaneous congruences
to the
simultaneous congruences 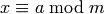 and
and 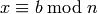 , if one exists. By the Chinese Remainder Theorem, a solution to the
simultaneous congruences exists if and only if
, if one exists. By the Chinese Remainder Theorem, a solution to the
simultaneous congruences exists if and only if
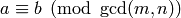 . The solution
. The solution  is only well-defined modulo
is only well-defined modulo
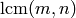 .
.
If a and b are lists, returns a simultaneous solution to
the congruences 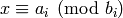 , if one exists.
, if one exists.
See also
EXAMPLES:
Using crt by giving it pairs of residues and moduli:
sage: crt(2, 1, 3, 5)
11
sage: crt(13, 20, 100, 301)
28013
sage: crt([2, 1], [3, 5])
11
sage: crt([13, 20], [100, 301])
28013
You can also use upper case:
sage: c = CRT(2,3, 3, 5); c
8
sage: c % 3 == 2
True
sage: c % 5 == 3
True
Note that this also works for polynomial rings:
sage: K.<a> = NumberField(x^3 - 7)
sage: R.<y> = K[]
sage: f = y^2 + 3
sage: g = y^3 - 5
sage: CRT(1,3,f,g)
-3/26*y^4 + 5/26*y^3 + 15/26*y + 53/26
sage: CRT(1,a,f,g)
(-3/52*a + 3/52)*y^4 + (5/52*a - 5/52)*y^3 + (15/52*a - 15/52)*y + 27/52*a + 25/52
You can also do this for any number of moduli:
sage: K.<a> = NumberField(x^3 - 7)
sage: R.<x> = K[]
sage: CRT([], [])
0
sage: CRT([a], [x])
a
sage: f = x^2 + 3
sage: g = x^3 - 5
sage: h = x^5 + x^2 - 9
sage: k = CRT([1, a, 3], [f, g, h]); k
(127/26988*a - 5807/386828)*x^9 + (45/8996*a - 33677/1160484)*x^8 + (2/173*a - 6/173)*x^7 + (133/6747*a - 5373/96707)*x^6 + (-6/2249*a + 18584/290121)*x^5 + (-277/8996*a + 38847/386828)*x^4 + (-135/4498*a + 42673/193414)*x^3 + (-1005/8996*a + 470245/1160484)*x^2 + (-1215/8996*a + 141165/386828)*x + 621/8996*a + 836445/386828
sage: k.mod(f)
1
sage: k.mod(g)
a
sage: k.mod(h)
3
If the moduli are not coprime, a solution may not exist:
sage: crt(4,8,8,12)
20
sage: crt(4,6,8,12)
...
ValueError: No solution to crt problem since gcd(8,12) does not divide 4-6
sage: x = polygen(QQ)
sage: crt(2,3,x-1,x+1)
-1/2*x + 5/2
sage: crt(2,x,x^2-1,x^2+1)
-1/2*x^3 + x^2 + 1/2*x + 1
sage: crt(2,x,x^2-1,x^3-1)
...
ValueError: No solution to crt problem since gcd(x^2 - 1,x^3 - 1) does not divide 2-x
Returns the  successive differences of the elements in
successive differences of the elements in
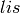 .
.
EXAMPLES:
sage: differences(prime_range(50))
[1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4]
sage: differences([i^2 for i in range(1,11)])
[3, 5, 7, 9, 11, 13, 15, 17, 19]
sage: differences([i^3 + 3*i for i in range(1,21)])
[10, 22, 40, 64, 94, 130, 172, 220, 274, 334, 400, 472, 550, 634, 724, 820, 922, 1030, 1144]
sage: differences([i^3 - i^2 for i in range(1,21)], 2)
[10, 16, 22, 28, 34, 40, 46, 52, 58, 64, 70, 76, 82, 88, 94, 100, 106, 112]
sage: differences([p - i^2 for i, p in enumerate(prime_range(50))], 3)
[-1, 2, -4, 4, -4, 4, 0, -6, 8, -6, 0, 4]
AUTHORS:
Returns a list of all positive integer divisors of the nonzero integer n.
INPUT:
EXAMPLES:
sage: divisors(-3)
[1, 3]
sage: divisors(6)
[1, 2, 3, 6]
sage: divisors(28)
[1, 2, 4, 7, 14, 28]
sage: divisors(2^5)
[1, 2, 4, 8, 16, 32]
sage: divisors(100)
[1, 2, 4, 5, 10, 20, 25, 50, 100]
sage: divisors(1)
[1]
sage: divisors(0)
...
ValueError: n must be nonzero
sage: divisors(2^3 * 3^2 * 17)
[1, 2, 3, 4, 6, 8, 9, 12, 17, 18, 24, 34, 36, 51, 68, 72, 102, 136, 153, 204, 306, 408, 612, 1224]
This function works whenever one has unique factorization:
sage: K.<a> = QuadraticField(7)
sage: divisors(K.ideal(7))
[Fractional ideal (1), Fractional ideal (-a), Fractional ideal (7)]
sage: divisors(K.ideal(3))
[Fractional ideal (1), Fractional ideal (3), Fractional ideal (a - 2), Fractional ideal (-a - 2)]
sage: divisors(K.ideal(35))
[Fractional ideal (1), Fractional ideal (35), Fractional ideal (-5*a), Fractional ideal (5), Fractional ideal (-a), Fractional ideal (7)]
TESTS:
sage: divisors(int(300))
[1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300]
Return a list of the primes 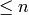 .
.
This is extremely slow and is for educational purposes only.
INPUT:
OUTPUT:
EXAMPLES:
sage: len(eratosthenes(100))
25
sage: eratosthenes(3)
[2, 3]
Returns the factorization of n. The result depends on the type of n.
If n is an integer, factor returns the factorization of the integer n as an object of type Factorization.
If n is not an integer, n.factor(proof=proof, **kwds) gets called. See n.factor?? for more documentation in this case.
Warning
This means that applying factor to an integer result of a symbolic computation will not factor the integer, because it is considered as an element of a larger symbolic ring.
EXAMPLE:
sage: f(n)=n^2
sage: is_prime(f(3))
False
sage: factor(f(3))
9
INPUT:
OUTPUT: factorization of n
The qsieve and ecm commands give access to highly optimized implementations of algorithms for doing certain integer factorization problems. These implementations are not used by the generic factor command, which currently just calls PARI (note that PARI also implements sieve and ecm algorithms, but they aren’t as optimized). Thus you might consider using them instead for certain numbers.
The factorization returned is an element of the class Factorization; see Factorization?? for more details, and examples below for usage. A Factorization contains both the unit factor (+1 or -1) and a sorted list of (prime, exponent) pairs.
The factorization displays in pretty-print format but it is easy to obtain access to the (prime,exponent) pairs and the unit, to recover the number from its factorization, and even to multiply two factorizations. See examples below.
EXAMPLES:
sage: factor(500)
2^2 * 5^3
sage: factor(-20)
-1 * 2^2 * 5
sage: f=factor(-20)
sage: list(f)
[(2, 2), (5, 1)]
sage: f.unit()
-1
sage: f.value()
-20
sage: factor(-500, algorithm='kash') # optional - kash
-1 * 2^2 * 5^3
sage: factor(-500, algorithm='magma') # optional - magma
-1 * 2^2 * 5^3
sage: factor(0)
...
ArithmeticError: Prime factorization of 0 not defined.
sage: factor(1)
1
sage: factor(-1)
-1
sage: factor(2^(2^7)+1)
59649589127497217 * 5704689200685129054721
Sage calls PARI’s factor, which has proof False by default. Sage has a global proof flag, set to True by default (see sage.structure.proof.proof, or proof.[tab]). To override the default, call this function with proof=False.
sage: factor(3^89-1, proof=False)
2 * 179 * 1611479891519807 * 5042939439565996049162197
sage: factor(2^197 + 1) # takes a long time (e.g., 3 seconds!)
3 * 197002597249 * 1348959352853811313 * 251951573867253012259144010843
To access the data in a factorization:
sage: f = factor(420); f
2^2 * 3 * 5 * 7
sage: [x for x in f]
[(2, 2), (3, 1), (5, 1), (7, 1)]
sage: [p for p,e in f]
[2, 3, 5, 7]
sage: [e for p,e in f]
[2, 1, 1, 1]
sage: [p^e for p,e in f]
[4, 3, 5, 7]
Compute the factorial of  , which is the product
, which is the product
 .
.
INPUT:
OUTPUT: an integer
EXAMPLES:
sage: from sage.rings.arith import factorial
sage: factorial(0)
1
sage: factorial(4)
24
sage: factorial(10)
3628800
sage: factorial(1) == factorial(0)
True
sage: factorial(6) == 6*5*4*3*2
True
sage: factorial(1) == factorial(0)
True
sage: factorial(71) == 71* factorial(70)
True
sage: factorial(-32)
...
ValueError: factorial -- must be nonnegative
PERFORMANCE: This discussion is valid as of April 2006. All timings below are on a Pentium Core Duo 2Ghz MacBook Pro running Linux with a 2.6.16.1 kernel.
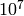 using the GMP algorithm, and the factorial of
using the GMP algorithm, and the factorial of
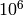 takes less than 4 seconds.
takes less than 4 seconds.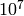 factorial in 100
seconds on the core duo 2Ghz.
factorial in 100
seconds on the core duo 2Ghz. 2.12-10 of
2.12-10 of
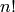 is best done using *[1..n]. It takes
113 seconds to compute the factorial of
is best done using *[1..n]. It takes
113 seconds to compute the factorial of 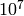 and 6
seconds to compute the factorial of
and 6
seconds to compute the factorial of 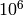 . Mathematica
V5.2 compute the factorial of
. Mathematica
V5.2 compute the factorial of 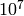 in 136 seconds and the
factorial of
in 136 seconds and the
factorial of 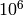 in 7 seconds. (Mathematica is notably
very efficient at memory usage when doing factorial
calculations.)
in 7 seconds. (Mathematica is notably
very efficient at memory usage when doing factorial
calculations.)Returns the falling factorial 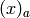 .
.
The notation in the literature is a mess: often 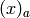 ,
but there are many other notations: GKP: Concrete Mathematics uses
,
but there are many other notations: GKP: Concrete Mathematics uses
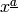 .
.
Definition: for integer 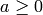 we have
we have
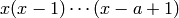 . In all other cases we use the
GAMMA-function:
. In all other cases we use the
GAMMA-function: 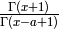 .
.
INPUT:
OR
OUTPUT: the falling factorial
EXAMPLES:
sage: falling_factorial(10, 3)
720
sage: falling_factorial(10, RR('3.0'))
720.000000000000
sage: falling_factorial(10, RR('3.3'))
1310.11633396601
sage: falling_factorial(10, 10)
3628800
sage: factorial(10)
3628800
sage: a = falling_factorial(1+I, I); a
gamma(I + 2)
sage: CC(a)
0.652965496420167 + 0.343065839816545*I
sage: falling_factorial(1+I, 4)
4*I + 2
sage: falling_factorial(I, 4)
-10
sage: M = MatrixSpace(ZZ, 4, 4)
sage: A = M([1,0,1,0,1,0,1,0,1,0,10,10,1,0,1,1])
sage: falling_factorial(A, 2) # A(A - I)
[ 1 0 10 10]
[ 1 0 10 10]
[ 20 0 101 100]
[ 2 0 11 10]
sage: x = ZZ['x'].0
sage: falling_factorial(x, 4)
x^4 - 6*x^3 + 11*x^2 - 6*x
AUTHORS:
Return the Farey sequence associated to the floating point number v.
INPUT:
OUTPUT: Results are (numerator, denominator); (1, 0) is “infinity”.
EXAMPLES:
sage: farey(2.0, 100)
(2, 1)
sage: farey(2.0, 1000)
(2, 1)
sage: farey(2.1, 1000)
(21, 10)
sage: farey(2.1, 100000)
(21, 10)
sage: farey(pi, 100000)
(312689, 99532)
AUTHORS:
Computes the decomposition into the sum of four squares, using an algorithm described by Peter Schorn at: http://www.schorn.ch/howto.html.
INPUT:
OUTPUT:
EXAMPLES:
sage: four_squares(3)
[0, 1, 1, 1]
sage: four_squares(130)
[0, 0, 3, 11]
sage: four_squares(1101011011004)
[2, 1049178, 2370, 15196]
sage: sum([i-sum([q^2 for q in four_squares(i)]) for i in range(2,10000)]) # long time
0
Return the discriminant of the quadratic extension
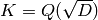 , i.e. an integer d congruent to either 0 or
1, mod 4, and such that, at most, the only square dividing it is
4.
, i.e. an integer d congruent to either 0 or
1, mod 4, and such that, at most, the only square dividing it is
4.
INPUT:
OUTPUT:
EXAMPLES:
sage: fundamental_discriminant(102)
408
sage: fundamental_discriminant(720)
5
sage: fundamental_discriminant(2)
8
Return the gaussian binomial

EXAMPLES:
sage: gaussian_binomial(5,1)
q^4 + q^3 + q^2 + q + 1
sage: gaussian_binomial(5,1).subs(q=2)
31
sage: gaussian_binomial(5,1,2)
31
AUTHORS:
The greatest common divisor of a and b, or if a is a list and b is omitted the greatest common divisor of all elements of a.
INPUT:
Additional keyword arguments are passed to the respectively called methods.
EXAMPLES:
sage: GCD(97,100)
1
sage: GCD(97*10^15, 19^20*97^2)
97
sage: GCD(2/3, 4/3)
1
sage: GCD([2,4,6,8])
2
sage: GCD(srange(0,10000,10)) # fast !!
10
Note that to take the gcd of  elements for
elements for 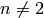 you must
put the elements into a list by enclosing them in [..]. Before
#4988 the following wrongly returned 3 since the third parameter
was just ignored:
you must
put the elements into a list by enclosing them in [..]. Before
#4988 the following wrongly returned 3 since the third parameter
was just ignored:
sage: gcd(3,6,2)
...
TypeError: gcd() takes at most 2 arguments (3 given)
sage: gcd([3,6,2])
1
Similarly, giving just one element (which is not a list) gives an error:
sage: gcd(3)
...
TypeError: 'sage.rings.integer.Integer' object is not iterable
By convention, the gcd of the empty list is (the integer) 0:
sage: gcd([])
0
sage: type(gcd([]))
<type 'sage.rings.integer.Integer'>
Return the fastest gcd function for integers of size no larger than order.
EXAMPLES:
sage: sage.rings.arith.get_gcd(4000)
<built-in method gcd_int of sage.rings.fast_arith.arith_int object at ...>
sage: sage.rings.arith.get_gcd(400000)
<built-in method gcd_longlong of sage.rings.fast_arith.arith_llong object at ...>
sage: sage.rings.arith.get_gcd(4000000000)
<function gcd at ...>
Return the fastest inverse_mod function for integers of size no larger than order.
EXAMPLES:
sage: sage.rings.arith.get_inverse_mod(6000)
<built-in method inverse_mod_int of sage.rings.fast_arith.arith_int object at ...>
sage: sage.rings.arith.get_inverse_mod(600000)
<built-in method inverse_mod_longlong of sage.rings.fast_arith.arith_llong object at ...>
sage: sage.rings.arith.get_inverse_mod(6000000000)
<function inverse_mod at ...>
This is the product of all (finite) primes where the Hilbert symbol is -1.
What is the same, this is the (reduced) discriminant of the quaternion
algebra 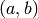 over
over  .
.
INPUT:
OUTPUT:
EXAMPLES:
sage: hilbert_conductor(-1, -1)
2
sage: hilbert_conductor(-1, -11)
11
sage: hilbert_conductor(-2, -5)
5
sage: hilbert_conductor(-3, -17)
17
AUTHOR:
Finds a pair of integers 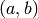 such that hilbert_conductor(a,b) == d.
The quaternion algebra
such that hilbert_conductor(a,b) == d.
The quaternion algebra 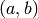 over
over  will then have (reduced)
discriminant
will then have (reduced)
discriminant 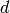 .
.
INPUT:
OUTPUT: pair of integers
EXAMPLES:
sage: hilbert_conductor_inverse(2)
(-1, -1)
sage: hilbert_conductor_inverse(3)
(-1, -3)
sage: hilbert_conductor_inverse(6)
(-1, 3)
sage: hilbert_conductor_inverse(30)
(-3, -10)
sage: hilbert_conductor_inverse(4)
...
ValueError: d needs to be squarefree
sage: hilbert_conductor_inverse(-1)
...
ValueError: d needs to be positive
AUTHOR:
TESTS:
sage: for i in xrange(100):
... d = ZZ.random_element(2**32).squarefree_part()
... if hilbert_conductor(*hilbert_conductor_inverse(d)) != d:
... print "hilbert_conductor_inverse failed for d =", d
Returns 1 if 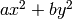
 -adically represents
a nonzero square, otherwise returns
-adically represents
a nonzero square, otherwise returns  . If either a or b
is 0, returns 0.
. If either a or b
is 0, returns 0.
INPUT:
OUTPUT: integer (0, -1, or 1)
EXAMPLES:
sage: hilbert_symbol (-1, -1, -1, algorithm='all')
-1
sage: hilbert_symbol (2,3, 5, algorithm='all')
1
sage: hilbert_symbol (4, 3, 5, algorithm='all')
1
sage: hilbert_symbol (0, 3, 5, algorithm='all')
0
sage: hilbert_symbol (-1, -1, 2, algorithm='all')
-1
sage: hilbert_symbol (1, -1, 2, algorithm='all')
1
sage: hilbert_symbol (3, -1, 2, algorithm='all')
-1
sage: hilbert_symbol(QQ(-1)/QQ(4), -1, 2) == -1
True
sage: hilbert_symbol(QQ(-1)/QQ(4), -1, 3) == 1
True
AUTHORS:
Return the ceiling of x.
EXAMPLES:
sage: integer_ceil(5.4)
6
Return the largest integer 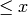 .
.
INPUT:
OUTPUT: an Integer
EXAMPLES:
sage: integer_floor(5.4)
5
sage: integer_floor(float(5.4))
5
sage: integer_floor(-5/2)
-3
sage: integer_floor(RDF(-5/2))
-3
The inverse of the ring element a modulo m.
If no special inverse_mod is defined for the elements, it tries to coerce them into integers and perform the inversion there
sage: inverse_mod(7,1)
0
sage: inverse_mod(5,14)
3
sage: inverse_mod(3,-5)
2
This function returns True if and only if  is a power of
2
is a power of
2
INPUT:
OUTPUT:
EXAMPLES:
sage: is_power_of_two(1024)
True
sage: is_power_of_two(1)
True
sage: is_power_of_two(24)
False
sage: is_power_of_two(0)
False
sage: is_power_of_two(-4)
False
AUTHORS:
Returns True if  is prime, and False otherwise.
is prime, and False otherwise.
AUTHORS:
INPUT:
OUTPUT:
EXAMPLES:
sage: is_prime(389)
True
sage: is_prime(2000)
False
sage: is_prime(2)
True
sage: is_prime(-1)
False
sage: factor(-6)
-1 * 2 * 3
sage: is_prime(1)
False
sage: is_prime(-2)
False
ALGORITHM:
Calculation is delegated to the n.is_prime() method, or in special cases (e.g., Python int``s) to ``Integer(n).is_prime(). If an n.is_prime() method is not available, it otherwise raises a TypeError.
Returns True if  is a prime power, and False otherwise.
The result is proven correct -
this is NOT a pseudo-primality test!.
is a prime power, and False otherwise.
The result is proven correct -
this is NOT a pseudo-primality test!.
INPUT:
EXAMPLES::
sage: is_prime_power(389)
True
sage: is_prime_power(2000)
False
sage: is_prime_power(2)
True
sage: is_prime_power(1024)
True
sage: is_prime_power(-1)
False
sage: is_prime_power(1)
True
sage: is_prime_power(997^100)
True
Returns True if  is a pseudo-prime, and False otherwise.
The result is NOT proven correct -
this is a pseudo-primality test!.
is a pseudo-prime, and False otherwise.
The result is NOT proven correct -
this is a pseudo-primality test!.
INPUT:
 is not a square mod x).
is not a square mod x).OUTPUT:
Note
We do not consider negatives of prime numbers as prime.
EXAMPLES::
sage: is_pseudoprime(389)
True
sage: is_pseudoprime(2000)
False
sage: is_pseudoprime(2)
True
sage: is_pseudoprime(-1)
False
sage: factor(-6)
-1 * 2 * 3
sage: is_pseudoprime(1)
False
sage: is_pseudoprime(-2)
False
IMPLEMENTATION: Calls the PARI ispseudoprime function.
Returns whether or not n is square, and if n is a square also returns the square root. If n is not square, also returns None.
INPUT:
OUTPUT:
EXAMPLES:
sage: is_square(2)
False
sage: is_square(4)
True
sage: is_square(2.2)
True
sage: is_square(-2.2)
False
sage: is_square(CDF(-2.2))
True
sage: is_square((x-1)^2)
True
sage: is_square(4, True)
(True, 2)
Returns True if and only if n is not divisible by the square of an integer > 1.
EXAMPLES:
sage: is_squarefree(100)
False
sage: is_squarefree(101)
True
Synonym for kronecker_symbol().
The Kronecker symbol 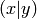 .
.
INPUT:
OUTPUT:
EXAMPLES:
sage: kronecker(3,5)
-1
sage: kronecker(3,15)
0
sage: kronecker(2,15)
1
sage: kronecker(-2,15)
-1
sage: kronecker(2/3,5)
1
The Kronecker symbol 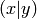 .
.
INPUT:
EXAMPLES:
sage: kronecker_symbol(13,21)
-1
sage: kronecker_symbol(101,4)
1
IMPLEMENTATION: Using GMP.
The least common multiple of a and b, or if a is a list and b is omitted the least common multiple of all elements of a.
Note that LCM is an alias for lcm.
INPUT:
EXAMPLES:
sage: lcm(97,100)
9700
sage: LCM(97,100)
9700
sage: LCM(0,2)
0
sage: LCM(-3,-5)
15
sage: LCM([1,2,3,4,5])
60
sage: v = LCM(range(1,10000)) # *very* fast!
sage: len(str(v))
4349
The Legendre symbol 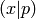 , for
, for  prime.
prime.
Note
The kronecker_symbol() command extends the Legendre
symbol to composite moduli and 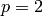 .
.
INPUT:
EXAMPLES:
sage: legendre_symbol(2,3)
-1
sage: legendre_symbol(1,3)
1
sage: legendre_symbol(1,2)
...
ValueError: p must be odd
sage: legendre_symbol(2,15)
...
ValueError: p must be a prime
sage: kronecker_symbol(2,15)
1
sage: legendre_symbol(2/3,7)
-1
Maximal Quotient Rational Reconstruction.
For research purposes only - this is pure Python, so slow.
INPUT:
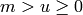 ,
, 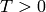 .
.OUTPUT:
Either integers 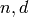 such that
such that 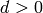 ,
, 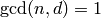 ,
,  , and
, and
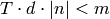 , or None.
, or None.
Reference: Monagan, Maximal Quotient Rational Reconstruction: An Almost Optimal Algorithm for Rational Reconstruction (page 11)
This algorithm is probabilistic.
EXAMPLES:
sage: mqrr_rational_reconstruction(21,3100,13)
(21, 1)
Return the multinomial coefficient
INPUT:
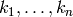
![[k_1,\dots,k_n]](../../_images/math/ff370dab2b483cffc9ee678597b36fe0e9a68bb8.png)
OUTPUT:
Returns the integer:
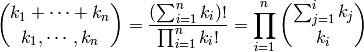
EXAMPLES:
sage: multinomial(0, 0, 2, 1, 0, 0)
3
sage: multinomial([0, 0, 2, 1, 0, 0])
3
sage: multinomial(3, 2)
10
sage: multinomial(2^30, 2, 1)
618970023101454657175683075
sage: multinomial([2^30, 2, 1])
618970023101454657175683075
AUTHORS:
Return a dictionary containing pairs
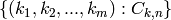 where
where
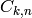 are multinomial coefficients such that
are multinomial coefficients such that
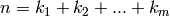 .
.
INPUT:
OUTPUT: dict
EXAMPLES:
sage: sorted(multinomial_coefficients(2,5).items())
[((0, 5), 1), ((1, 4), 5), ((2, 3), 10), ((3, 2), 10), ((4, 1), 5), ((5, 0), 1)]
Notice that these are the coefficients of 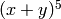 :
:
sage: R.<x,y> = QQ[]
sage: (x+y)^5
x^5 + 5*x^4*y + 10*x^3*y^2 + 10*x^2*y^3 + 5*x*y^4 + y^5
sage: sorted(multinomial_coefficients(3,2).items())
[((0, 0, 2), 1), ((0, 1, 1), 2), ((0, 2, 0), 1), ((1, 0, 1), 2), ((1, 1, 0), 2), ((2, 0, 0), 1)]
ALGORITHM: The algorithm we implement for computing the multinomial coefficients is based on the following result:
Consider a polynomial and its  -th exponent:
-th exponent:
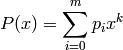
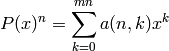
We compute the coefficients 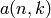 using the J.C.P.
Miller Pure Recurrence [see D.E.Knuth, Seminumerical Algorithms,
The art of Computer Programming v.2, Addison Wesley, Reading,
1981].
using the J.C.P.
Miller Pure Recurrence [see D.E.Knuth, Seminumerical Algorithms,
The art of Computer Programming v.2, Addison Wesley, Reading,
1981].
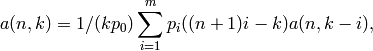
where 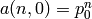 .
.
AUTHORS:
The next prime greater than the integer n. If n is prime, then this function does not return n, but the next prime after n. If the optional argument proof is False, this function only returns a pseudo-prime, as defined by the PARI nextprime function. If it is None, uses the global default (see sage.structure.proof.proof)
INPUT:
EXAMPLES:
sage: next_prime(-100)
2
sage: next_prime(1)
2
sage: next_prime(2)
3
sage: next_prime(3)
5
sage: next_prime(4)
5
Notice that the next_prime(5) is not 5 but 7.
sage: next_prime(5)
7
sage: next_prime(2004)
2011
The next prime power greater than the integer n. If n is a prime power, then this function does not return n, but the next prime power after n.
EXAMPLES:
sage: next_prime_power(-10)
1
sage: is_prime_power(1)
True
sage: next_prime_power(0)
1
sage: next_prime_power(1)
2
sage: next_prime_power(2)
3
sage: next_prime_power(10)
11
sage: next_prime_power(7)
8
sage: next_prime_power(99)
101
Returns the next probable prime after self, as determined by PARI.
INPUT:
EXAMPLES:
sage: next_probable_prime(-100)
2
sage: next_probable_prime(19)
23
sage: next_probable_prime(int(999999999))
1000000007
sage: next_probable_prime(2^768)
1552518092300708935148979488462502555256886017116696611139052038026050952686376886330878408828646477950487730697131073206171580044114814391444287275041181139204454976020849905550265285631598444825262999193716468750892846853816058039
EXAMPLES:
sage: nth_prime(3)
5
sage: nth_prime(10)
29
sage: nth_prime(0)
...
ValueError: nth prime meaningless for non-positive n (=0)
Return the number of divisors of the integer n.
INPUT:
OUTPUT:
EXAMPLES:
sage: number_of_divisors(100)
9
sage: number_of_divisors(-720)
30
The odd part of the integer  . This is
. This is 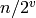 ,
where
,
where  .
.
EXAMPLES:
sage: odd_part(5)
5
sage: odd_part(4)
1
sage: odd_part(factorial(31))
122529844256906551386796875
The n-th power of a modulo the integer m.
EXAMPLES:
sage: power_mod(0,0,5)
...
ArithmeticError: 0^0 is undefined.
sage: power_mod(2,390,391)
285
sage: power_mod(2,-1,7)
4
sage: power_mod(11,1,7)
4
sage: R.<x> = ZZ[]
sage: power_mod(3*x, 10, 7)
4*x^10
sage: power_mod(11,1,0)
...
ZeroDivisionError: modulus must be nonzero.
The largest prime < n. The result is provably correct. If n <= 1, this function raises a ValueError.
EXAMPLES:
sage: previous_prime(10)
7
sage: previous_prime(7)
5
sage: previous_prime(8)
7
sage: previous_prime(7)
5
sage: previous_prime(5)
3
sage: previous_prime(3)
2
sage: previous_prime(2)
...
ValueError: no previous prime
sage: previous_prime(1)
...
ValueError: no previous prime
sage: previous_prime(-20)
...
ValueError: no previous prime
The largest prime power 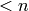 . The result is provably
correct. If
. The result is provably
correct. If 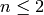 , this function returns
, this function returns 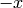 ,
where
,
where  is prime power and
is prime power and 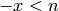 and no larger
negative of a prime power has this property.
and no larger
negative of a prime power has this property.
EXAMPLES:
sage: previous_prime_power(2)
1
sage: previous_prime_power(10)
9
sage: previous_prime_power(7)
5
sage: previous_prime_power(127)
125
sage: previous_prime_power(0)
...
ValueError: no previous prime power
sage: previous_prime_power(1)
...
ValueError: no previous prime power
sage: n = previous_prime_power(2^16 - 1)
sage: while is_prime(n):
... n = previous_prime_power(n)
sage: factor(n)
251^2
The prime divisors of the integer n, sorted in increasing order. If n is negative, we do not include -1 among the prime divisors, since -1 is not a prime number.
EXAMPLES:
sage: prime_divisors(1)
[]
sage: prime_divisors(100)
[2, 5]
sage: prime_divisors(-100)
[2, 5]
sage: prime_divisors(2004)
[2, 3, 167]
The prime divisors of the integer n, sorted in increasing order. If n is negative, we do not include -1 among the prime divisors, since -1 is not a prime number.
EXAMPLES:
sage: prime_divisors(1)
[]
sage: prime_divisors(100)
[2, 5]
sage: prime_divisors(-100)
[2, 5]
sage: prime_divisors(2004)
[2, 3, 167]
List of all positive primes powers between start and stop-1, inclusive. If the second argument is omitted, returns the primes up to the first argument.
EXAMPLES:
sage: prime_powers(20)
[1, 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19]
sage: len(prime_powers(1000))
194
sage: len(prime_range(1000))
168
sage: a = [z for z in range(95,1234) if is_prime_power(z)]
sage: b = prime_powers(95,1234)
sage: len(b)
194
sage: len(a)
194
sage: a[:10]
[97, 101, 103, 107, 109, 113, 121, 125, 127, 128]
sage: b[:10]
[97, 101, 103, 107, 109, 113, 121, 125, 127, 128]
sage: a == b
True
TESTS:
sage: v = prime_powers(10)
sage: type(v[0]) # trac #922
<type 'sage.rings.integer.Integer'>
Returns the prime-to-m part of n, i.e., the largest divisor of n that is coprime to m.
INPUT:
OUTPUT: Integer
EXAMPLES:
sage: z = 43434
sage: z.prime_to_m_part(20)
21717
Returns an iterator over all primes between start and stop-1, inclusive. This is much slower than prime_range, but potentially uses less memory.
This command is like the xrange command, except it only iterates over primes. In some cases it is better to use primes than prime_range, because primes does not build a list of all primes in the range in memory all at once. However it is potentially much slower since it simply calls the next_prime function repeatedly, and next_prime is slow, partly because it proves correctness.
EXAMPLES:
sage: for p in primes(5,10):
... print p
...
5
7
sage: list(primes(11))
[2, 3, 5, 7]
sage: list(primes(10000000000, 10000000100))
[10000000019, 10000000033, 10000000061, 10000000069, 10000000097]
Return the first  primes.
primes.
INPUT:
 - a nonnegative integer
- a nonnegative integerOUTPUT:
 prime numbers.
prime numbers.EXAMPLES:
sage: primes_first_n(10)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
sage: len(primes_first_n(1000))
1000
sage: primes_first_n(0)
[]
Return a generator for the multiplicative group of integers modulo
 , if one exists.
, if one exists.
EXAMPLES:
sage: primitive_root(23)
5
sage: print [primitive_root(p) for p in primes(100)]
[1, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 6, 3, 5, 2, 2, 2, 2, 7, 5, 3, 2, 3, 5]
Return a sorted list of all squares modulo the integer  in the range
in the range 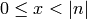 .
.
EXAMPLES:
sage: quadratic_residues(11)
[0, 1, 3, 4, 5, 9]
sage: quadratic_residues(1)
[0]
sage: quadratic_residues(2)
[0, 1]
sage: quadratic_residues(8)
[0, 1, 4]
sage: quadratic_residues(-10)
[0, 1, 4, 5, 6, 9]
sage: v = quadratic_residues(1000); len(v);
159
Returns a random prime p between 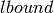 and n (i.e.
and n (i.e. 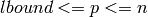 ).
The returned prime is chosen uniformly at random from the set of prime
numbers less than or equal to n.
).
The returned prime is chosen uniformly at random from the set of prime
numbers less than or equal to n.
INPUT:
EXAMPLES:
sage: random_prime(100000)
88237
sage: random_prime(2)
2
TESTS:
sage: type(random_prime(2))
<type 'sage.rings.integer.Integer'>
sage: type(random_prime(100))
<type 'sage.rings.integer.Integer'>
AUTHORS:
This function tries to compute  , where
, where  is a rational number in
lowest terms such that the reduction of
is a rational number in
lowest terms such that the reduction of  modulo
modulo 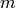 is equal to
is equal to  and
the absolute values of
and
the absolute values of  and
and 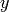 are both
are both 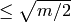 . If such
. If such  exists, that pair is unique and this function returns it. If no
such pair exists, this function raises ZeroDivisionError.
exists, that pair is unique and this function returns it. If no
such pair exists, this function raises ZeroDivisionError.
An efficient algorithm for computing rational reconstruction is very similar to the extended Euclidean algorithm. For more details, see Knuth, Vol 2, 3rd ed, pages 656-657.
INPUT:
OUTPUT:
Numerator and denominator  ,
, 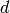 of the unique rational number
of the unique rational number
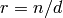 , if it exists, with
, if it exists, with  and
and 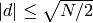 . Return
. Return
 if no such number exists.
if no such number exists.
The algorithm for rational reconstruction is described (with a complete nontrivial proof) on pages 656-657 of Knuth, Vol 2, 3rd ed. as the solution to exercise 51 on page 379. See in particular the conclusion paragraph right in the middle of page 657, which describes the algorithm thus:
This discussion proves that the problem can be solved efficiently by applying Algorithm 4.5.2X withand
, but with the following replacement for step X2: If
, the algorithm terminates. The pair
is then the unique solution, provided that
and
are coprime and
; otherwise there is no solution. (Alg 4.5.2X is the extended Euclidean algorithm.)
Knuth remarks that this algorithm is due to Wang, Kornerup, and Gregory from around 1983.
EXAMPLES:
sage: m = 100000
sage: (119*inverse_mod(53,m))%m
11323
sage: rational_reconstruction(11323,m)
119/53
sage: rational_reconstruction(400,1000)
...
ValueError: Rational reconstruction of 400 (mod 1000) does not exist.
sage: rational_reconstruction(3,292393, algorithm='python')
3
sage: a = Integers(292393)(45/97); a
204977
sage: rational_reconstruction(a,292393, algorithm='python')
45/97
sage: a = Integers(292393)(45/97); a
204977
sage: rational_reconstruction(a,292393, algorithm='fast')
45/97
sage: rational_reconstruction(293048,292393, algorithm='fast')
...
ValueError: Rational reconstruction of 655 (mod 292393) does not exist.
sage: rational_reconstruction(293048,292393, algorithm='python')
...
ValueError: Rational reconstruction of 655 (mod 292393) does not exist.
Returns the rising factorial  .
.
The notation in the literature is a mess: often  ,
but there are many other notations: GKP: Concrete Mathematics uses
,
but there are many other notations: GKP: Concrete Mathematics uses
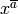 .
.
The rising factorial is also known as the Pochhammer symbol, see Maple and Mathematica.
Definition: for integer 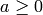 we have
we have
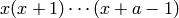 . In all other cases we use the
GAMMA-function:
. In all other cases we use the
GAMMA-function:  .
.
INPUT:
OUTPUT: the rising factorial
EXAMPLES:
sage: rising_factorial(10,3)
1320
sage: rising_factorial(10,RR('3.0'))
1320.00000000000
sage: rising_factorial(10,RR('3.3'))
2826.38895824964
sage: a = rising_factorial(1+I, I); a
gamma(2*I + 1)/gamma(I + 1)
sage: CC(a)
0.266816390637832 + 0.122783354006372*I
sage: a = rising_factorial(I, 4); a
-10
See falling_factorial(I, 4).
sage: x = polygen(ZZ)
sage: rising_factorial(x, 4)
x^4 + 6*x^3 + 11*x^2 + 6*x
AUTHORS:
Given a list of complex numbers (or a list of tuples, where the first element of each tuple is a complex number), we sort the list in a “pretty” order. First come the real numbers (with zero imaginary part), then the complex numbers sorted according to their real part. If two complex numbers have a real part which is sufficiently close, then they are sorted according to their imaginary part.
This is not a useful function mathematically (not least because there’s no principled way to determine whether the real components should be treated as equal or not). It is called by various polynomial root-finders; its purpose is to make doctest printing more reproducible.
We deliberately choose a cumbersome name for this function to discourage use, since it is mathematically meaningless.
EXAMPLES:
sage: import sage.rings.arith
sage: sort_c = sort_complex_numbers_for_display
sage: nums = [CDF(i) for i in range(3)]
sage: for i in range(3):
... nums.append(CDF(i + RDF.random_element(-3e-11, 3e-11),
... RDF.random_element()))
... nums.append(CDF(i + RDF.random_element(-3e-11, 3e-11),
... RDF.random_element()))
sage: shuffle(nums)
sage: sort_c(nums)
[0, 1.0, 2.0, -2.862406201e-11 - 0.708874026302*I, 2.2108362707e-11 - 0.436810529675*I, 1.00000000001 - 0.758765473764*I, 0.999999999976 - 0.723896589334*I, 1.99999999999 - 0.456080101207*I, 1.99999999999 + 0.609083628313*I]
Iterator over the squarefree divisors (up to units) of the element x.
Depends on the output of the prime_divisors function.
INPUT:
x -- an element of any ring for which the prime_divisors
function works.
EXAMPLES:
sage: list(squarefree_divisors(7))
[1, 7]
sage: list(squarefree_divisors(6))
[1, 2, 3, 6]
sage: list(squarefree_divisors(12))
[1, 2, 3, 6]
Subfactorial or rencontres numbers, or derangements: number of
permutations of  elements with no fixed points.
elements with no fixed points.
INPUT:
OUTPUT:
EXAMPLES:
sage: subfactorial(0)
1
sage: subfactorial(1)
0
sage: subfactorial(8)
14833
AUTHORS:
Return the smallest prime divisor <= bound of the positive integer n, or n if there is no such prime. If the optional argument bound is omitted, then bound <= n.
INPUT:
OUTPUT:
EXAMPLES:
sage: trial_division(15)
3
sage: trial_division(91)
7
sage: trial_division(11)
11
sage: trial_division(387833, 300)
387833
sage: # 300 is not big enough to split off a
sage: # factor, but 400 is.
sage: trial_division(387833, 400)
389
Write the integer n as a sum of two integer squares if possible; otherwise raise a ValueError.
EXAMPLES:
sage: two_squares(389)
(10, 17)
sage: two_squares(7)
...
ValueError: 7 is not a sum of two squares
sage: a,b = two_squares(2009); a,b
(28, 35)
sage: a^2 + b^2
2009
TODO: Create an implementation using PARI’s continued fraction implementation.
The exact power of p that divides m.
m should be an integer or rational (but maybe other types work too.)
This actually just calls the m.valuation() method.
If m is 0, this function returns rings.infinity.
EXAMPLES:
sage: valuation(512,2)
9
sage: valuation(1,2)
0
sage: valuation(5/9, 3)
-2
Valuation of 0 is defined, but valuation with respect to 0 is not:
sage: valuation(0,7)
+Infinity
sage: valuation(3,0)
...
ValueError: You can only compute the valuation with respect to a integer larger than 1.
Here are some other examples:
sage: valuation(100,10)
2
sage: valuation(200,10)
2
sage: valuation(243,3)
5
sage: valuation(243*10007,3)
5
sage: valuation(243*10007,10007)
1
Return a triple (g,s,t) such that 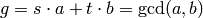 .
.
Note
One exception is if  and
and 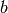 are not in a PID, e.g., they are
both polynomials over the integers, then this function can’t in
general return (g,s,t) as above, since they need not exist.
Instead, over the integers, we first multiply
are not in a PID, e.g., they are
both polynomials over the integers, then this function can’t in
general return (g,s,t) as above, since they need not exist.
Instead, over the integers, we first multiply 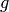 by a divisor of
the resultant of
by a divisor of
the resultant of 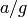 and
and  , up to sign.
, up to sign.
INPUT:
OUTPUT:

Note
There is no guarantee that the returned cofactors (s and t) are minimal. In the integer case, see sage.rings.integer.Integer._xgcd() for minimal cofactors.
EXAMPLES:
sage: xgcd(56, 44)
(4, 4, -5)
sage: 4*56 + (-5)*44
4
sage: g, a, b = xgcd(5/1, 7/1); g, a, b
(1, 3, -2)
sage: a*(5/1) + b*(7/1) == g
True
sage: x = polygen(QQ)
sage: xgcd(x^3 - 1, x^2 - 1)
(x - 1, 1, -x)
sage: K.<g> = NumberField(x^2-3)
sage: R.<a,b> = K[]
sage: S.<y> = R.fraction_field()[]
sage: xgcd(y^2, a*y+b)
(1, a^2/b^2, ((-a)/b^2)*y + 1/b)
sage: xgcd((b+g)*y^2, (a+g)*y+b)
(1, (a^2 + (2*g)*a + 3)/(b^3 + (g)*b^2), ((-a + (-g))/b^2)*y + 1/b)
We compute an xgcd over the integers, where the linear combination is not the gcd but the resultant:
sage: R.<x> = ZZ[]
sage: gcd(2*x*(x-1), x^2)
x
sage: xgcd(2*x*(x-1), x^2)
(2*x, -1, 2)
sage: (2*(x-1)).resultant(x)
2
Extended lcm function: given two positive integers 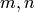 , returns
a triple
, returns
a triple  such that
such that 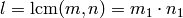 where
where 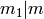 ,
, 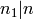 and
and 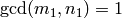 , all with no
factorization.
, all with no
factorization.
Used to construct an element of order 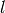 from elements of orders
from elements of orders 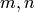 in any group: see sage/groups/generic.py for examples.
in any group: see sage/groups/generic.py for examples.
EXAMPLES:
sage: xlcm(120,36)
(360, 40, 9)