Parametric Surface

Graphics 3D object for triangulating surfaces, and a base class for many other objects that can be represented by a 2D parametrization.

It takes great care to turn degenerate quadrilaterals into triangles and to propagate identified points to all attached polygons. This is not so much to save space as it is to assist the raytracers/other rendering systems to better understand the surface (and especially calculate correct surface normals).

AUTHORS:

• Robert Bradshaw (2007-08-26): initial version

EXAMPLES:

sage: from sage.plot.plot3d.parametric_surface import ParametricSurface, MobiusStrip
sage: def f(x,y): return x+y, sin(x)*sin(y), x*y
sage: P = ParametricSurface(f, (srange(0,10,0.1), srange(-5,5.0,0.1)))
sage: show(P)
sage: S = MobiusStrip(1,.2)
sage: S.is_enclosed()
False
sage: S.show()

Note

One may override eval() or eval_c() in a subclass rather than passing in a function for greater speed. One also would want to override get_grid.

TODO: actually remove unused points, fix the below code:

S = ParametricSurface(f=(lambda (x,y):(x,y,0)), domain=(range(10),range(10)))

class sage.plot.plot3d.parametric_surface.MobiusStrip

Bases: sage.plot.plot3d.parametric_surface.ParametricSurface

Base class for the MobiusStrip graphics type. This sets the the basic parameters of the object.

INPUT:

• r - A number which can be coerced to a float, serving roughly as the radius of the object.
• width - A number which can be coerced to a float, which gives the width of the object.
• twists - (default: 1) An integer, giving the number of twists in the object (where one twist is the ‘traditional’ Mobius strip).

EXAMPLES:

sage: from sage.plot.plot3d.parametric_surface import MobiusStrip
sage: M = MobiusStrip(3,3)
sage: M.show()

eval(u, v)

Returns tuple for 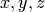coordinates for the given u and v for this MobiusStrip instance.

EXAMPLE:

sage: from sage.plot.plot3d.parametric_surface import MobiusStrip
sage: N = MobiusStrip(7,3,2) # two twists
sage: N.eval(-1,0)
(4.0, 0.0, -0.0)

get_grid(ds)

Returns appropriate and ranges for this MobiusStrip instance. This is intended for internal use in creating an actual plot.

INPUT:

• ds - A number, typically coming from a RenderParams object, which helps determine the increment for the range for the MobiusStrip object.

EXAMPLE:

sage: from sage.plot.plot3d.parametric_surface import MobiusStrip
sage: N = MobiusStrip(7,3,2) # two twists
sage: N.get_grid(N.default_render_params().ds)
([-1, 1], [0.0, 0.125663706144, 0.251327412287, 0.376991118431, ... 0])

class sage.plot.plot3d.parametric_surface.ParametricSurface

Bases: sage.plot.plot3d.index_face_set.IndexFaceSet

Base class that initializes the ParametricSurface graphics type. This sets options, the function to be plotted, and the plotting array as attributes.

INPUT:

• f - (default: None) The defining function. Either a tuple of three functions, or a single function which returns a tuple, taking two python floats as input. To subclass, pass None for f and override eval_c or eval instead.
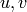• domain - (default: None) A tuple of two lists, defining the grid of values. If None, this will be calculate automatically.

EXAMPLES:

sage: from sage.plot.plot3d.parametric_surface import ParametricSurface
sage: def f(x,y): return cos(x)*sin(y), sin(x)*sin(y), cos(y)+log(tan(y/2))+0.2*x
sage: S = ParametricSurface(f, (srange(0,12.4,0.1), srange(0.1,2,0.1)))
sage: show(S)

sage: len(S.face_list())
2214

The Hessenberg surface:

sage: def f(u,v):
...       a = 1
...       from math import cos, sin, sinh, cosh
...       x = cos(a)*(cos(u)*sinh(v)-cos(3*u)*sinh(3*v)/3) + sin(a)*(
...           sin(u)*cosh(v)-sin(3*u)*cosh(3*v)/3)
...       y = cos(a)*(sin(u)*sinh(v)+sin(3*u)*sinh(3*v)/3) + sin(a)*(
...           -cos(u)*cosh(v)-cos(3*u)*cosh(3*v)/3)
...       z = cos(a)*cos(2*u)*cosh(2*v)+sin(a)*sin(2*u)*sinh(2*v)
...       return (x,y,z)
sage: v = srange(float(0),float((3/2)*pi),float(0.1))
sage: S = ParametricSurface(f, (srange(float(0),float(pi),float(0.1)),
...                  srange(float(-1),float(1),float(0.1))), color="blue")
sage: show(S)    

bounding_box()

Returns the lower and upper corners of a 3D bounding box for self. This is used for rendering and self should fit entirely within this box.

Specifically, the first point returned should have x, y, and z coordinates should be the respective infimum over all points in self, and the second point is the supremum.

EXAMPLES:

sage: from sage.plot.plot3d.parametric_surface import MobiusStrip
sage: M = MobiusStrip(7,3,2)
sage: M.bounding_box()
((-10.0, -7.5390734925047846, -2.9940801852848145), (10.0, 7.5390734925047846, 2.9940801852848145))

default_render_params()

Returns an instance of RenderParams suitable for plotting this object.

TEST:

sage: from sage.plot.plot3d.parametric_surface import MobiusStrip
sage: type(MobiusStrip(3,3).default_render_params())
<class 'sage.plot.plot3d.base.RenderParams'>

dual()

Returns an IndexFaceSet which is the dual of the ParametricSurface object as a triangulated surface.

EXAMPLES:

As one might expect, this gives an icosahedron:

sage: D = dodecahedron()
sage: D.dual()

But any enclosed surface should work:

sage: from sage.plot.plot3d.shapes import Torus
sage: T =  Torus(1, .2)
sage: T.dual()
sage: T.is_enclosed()
True

Surfaces which are not enclosed, though, should raise an exception:

sage: from sage.plot.plot3d.parametric_surface import MobiusStrip
sage: M = MobiusStrip(3,1)
sage: M.is_enclosed()
False
sage: M.dual()
...
NotImplementedError: This is only implemented for enclosed surfaces

eval(u, v)

TEST:

sage: from sage.plot.plot3d.parametric_surface import ParametricSurface
sage: def f(x,y): return x+y,x-y,x*y
sage: P = ParametricSurface(f,(srange(0,1,0.1),srange(0,1,0.1)))
sage: P.eval(0,0)
...
NotImplementedError

get_grid(ds)

TEST:

sage: from sage.plot.plot3d.parametric_surface import ParametricSurface
sage: def f(x,y): return x+y,x-y,x*y
sage: P = ParametricSurface(f)
sage: P.get_grid(.1)
...
NotImplementedError: You must override the get_grid method.

is_enclosed()

Returns a boolean telling whether or not it is necessary to render the back sides of the polygons (assuming, of course, that they have the correct orientation).

This is calculated in by verifying the opposite edges of the rendered domain either line up or are pinched together.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Sphere
sage: Sphere(1).is_enclosed()
True

sage: from sage.plot.plot3d.parametric_surface import MobiusStrip
sage: MobiusStrip(1,0.2).is_enclosed()
False

jmol_repr(render_params)

Returns representation of the object suitable for plotting using Jmol.

TESTS:

sage: _ = var('x,y')
sage: P = plot3d(x^2-y^2, (x, -2, 2), (y, -2, 2))
sage: s = P.jmol_repr(P.testing_render_params())
sage: s[:10]
['pmesh obj_1 "obj_1.pmesh"\ncolor pmesh  [102,102,255]']

json_repr(render_params)

Returns representation of the object in JSON format as a list with one element, which is a string of a dictionary listing vertices and faces.

TESTS:

sage: _ = var('x,y')
sage: P = plot3d(x^2-y^2, (x, -2, 2), (y, -2, 2))
sage: s = P.json_repr(P.default_render_params())
sage: s[0][:100]
'{vertices:[{x:-2,y:-2,z:0},{x:-2,y:-1.89744,z:0.399737},{x:-2,y:-1.79487,z:0.778435},{x:-2,y:-1.6923'

obj_repr(render_params)

Returns complete representation of object with name, texture, and lists of vertices, faces, and back-faces.

TESTS:

sage: _ = var('x,y')
sage: P = plot3d(x^2-y^2, (x, -2, 2), (y, -2, 2))
sage: s = P.obj_repr(P.default_render_params())
sage: s[:2]+s[2][:3]+s[3][:3]
['g obj_1', 'usemtl texture230', 'v -2 -2 0', 'v -2 -1.89744 0.399737', 'v -2 -1.79487 0.778435', 'f 1 2 42 41', 'f 2 3 43 42', 'f 3 4 44 43']

tachyon_repr(render_params)

Returns representation of the object suitable for plotting using Tachyon ray tracer.

TESTS:

sage: _ = var('x,y')
sage: P = plot3d(x^2-y^2, (x, -2, 2), (y, -2, 2))
sage: s = P.tachyon_repr(P.default_render_params())
sage: s[:2]
['TRI V0 -2 -2 0 V1 -2 -1.89744 0.399737 V2 -1.89744 -1.89744 0', 'texture229']

triangulate(render_params=None)

Calls self.eval_grid() for all 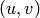in 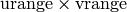to construct this surface.

The most complicated part of this code is identifying shared vertices and shrinking trivial edges. This is not done so much to save memory, rather it is needed so normals of the triangles can be calculated correctly.

TESTS:

sage: from sage.plot.plot3d.parametric_surface import ParametricSurface, MobiusStrip
sage: def f(x,y): return x+y, sin(x)*sin(y), x*y                        # indirect doctests
sage: P = ParametricSurface(f, (srange(0,10,0.1), srange(-5,5.0,0.1)))  # indirect doctests
sage: P.show()                                                          # indirect doctests
sage: S = MobiusStrip(1,.2)                                             # indirect doctests
sage: S.show()                                                          # indirect doctests

x3d_geometry()

Returns XML-like representation of the coordinates of all points in a triangulation of the object along with an indexing of those points.

TESTS:

sage: _ = var('x,y')
sage: P = plot3d(x^2-y^2, (x, -2, 2), (y, -2, 2))
sage: s = P.x3d_str()
sage: s[:100]
"<Shape>\n<IndexedFaceSet coordIndex='0,1,..."