AUTHOR:
Solves the bin packing problem.
The Bin Packing problem is the following :
Given a list of items of weights 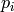 and a real value
and a real value  , what is
the least number of bins such that all the items can be put in the
bins, while keeping sure that each bin contains a weight of at most
, what is
the least number of bins such that all the items can be put in the
bins, while keeping sure that each bin contains a weight of at most  ?
?
For more informations : http://en.wikipedia.org/wiki/Bin_packing_problem
 bins ?
bins ?INPUT:
 bins if possible, and raises an
exception otherwise.
bins if possible, and raises an
exception otherwise.OUTPUT:
A list of lists, each member corresponding to a box and containing the list of the weights inside it. If there is no solution, an exception is raised (this can only happen when k is specified or if maximum is less that the size of one item).
EXAMPLES:
Trying to find the minimum amount of boxes for 5 items of weights
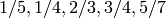 :
:
sage: from sage.numerical.optimize import binpacking
sage: values = [1/5, 1/3, 2/3, 3/4, 5/7]
sage: bins = binpacking(values)
sage: len(bins)
3
Checking the bins are of correct size
sage: all([ sum(b)<= 1 for b in bins ])
True
Checking every item is in a bin
sage: b1, b2, b3 = bins
sage: all([ (v in b1 or v in b2 or v in b3) for v in values ])
True
One way to use only three boxes (which is best possible) is to put
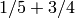 together in a box,
together in a box, 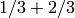 in another, and
in another, and 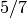 by itself in the third one.
by itself in the third one.
Of course, we can also check that there is no solution using only two boxes
sage: from sage.numerical.optimize import binpacking
sage: binpacking([0.2,0.3,0.8,0.9], k=2)
...
ValueError: This problem has no solution !
Finds numerical estimates for the parameters of the function model to give a best fit to data.
INPUT:
![[[x_{1,1}, x_{1,2}, \ldots, x_{1,k}, f_1],
[x_{2,1}, x_{2,2}, \ldots, x_{2,k}, f_2],
\ldots,
[x_{n,1}, x_{n,2}, \ldots, x_{n,k}, f_n]]](../../_images/math/d09fa9b0f51244c6d469e61e937d485b6dbb9960.png) given as either a list of
lists, matrix, or numpy array.
given as either a list of
lists, matrix, or numpy array.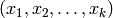 and free parameters
and free parameters
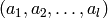 .
.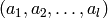 , given as either a list, tuple,
vector or numpy array. If None, the default estimate for each
parameter is
, given as either a list, tuple,
vector or numpy array. If None, the default estimate for each
parameter is  .
.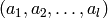 . If model is a symbolic function it is
ignored, and the free parameters of the symbolic function are used.
. If model is a symbolic function it is
ignored, and the free parameters of the symbolic function are used.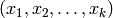 . If model is a symbolic function it is
ignored, and the variables of the symbolic function are used.
. If model is a symbolic function it is
ignored, and the variables of the symbolic function are used.EXAMPLES:
First we create some data points of a sine function with some random perturbations:
sage: data = [(i, 1.2 * sin(0.5*i-0.2) + 0.1 * normalvariate(0, 1)) for i in xsrange(0, 4*pi, 0.2)]
sage: var('a, b, c, x')
(a, b, c, x)
We define a function with free parameters  ,
,  and
and  :
:
sage: model(x) = a * sin(b * x - c)
We search for the parameters that give the best fit to the data:
sage: find_fit(data, model)
[a == 1.21..., b == 0.49..., c == 0.19...]
We can also use a Python function for the model:
sage: def f(x, a, b, c): return a * sin(b * x - c)
sage: fit = find_fit(data, f, parameters = [a, b, c], variables = [x], solution_dict = True)
sage: fit[a], fit[b], fit[c]
(1.21..., 0.49..., 0.19...)
We search for a formula for the  -th prime number:
-th prime number:
sage: dataprime = [(i, nth_prime(i)) for i in xrange(1, 5000, 100)]
sage: find_fit(dataprime, a * x * log(b * x), parameters = [a, b], variables = [x])
[a == 1.11..., b == 1.24...]
ALGORITHM:
Uses scipy.optimize.leastsq which in turn uses MINPACK’s lmdif and lmder algorithms.
Numerically find the maximum of the expression  on the interval
on the interval
![[a,b]](../../_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) (or
(or ![[b,a]](../../_images/math/a5aa84566486814ea5e952727df5d17a1b168480.png) ) along with the point at which the maximum is attained.
) along with the point at which the maximum is attained.
See the documentation for find_minimum_on_interval() for more details.
EXAMPLES:
sage: f = lambda x: x*cos(x)
sage: find_maximum_on_interval(f, 0,5)
(0.561096338191..., 0.8603335890...)
sage: find_maximum_on_interval(f, 0,5, tol=0.1, maxfun=10)
(0.561090323458..., 0.857926501456...)
Numerically find the minimum of the expression f on the
interval ![[a,b]](../../_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) (or
(or ![[b,a]](../../_images/math/a5aa84566486814ea5e952727df5d17a1b168480.png) ) and the point at which it attains that
minimum. Note that f must be a function of (at most) one
variable.
) and the point at which it attains that
minimum. Note that f must be a function of (at most) one
variable.
INPUT:
OUTPUT:
![[a,b]](../../_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png)
EXAMPLES:
sage: f = lambda x: x*cos(x)
sage: find_minimum_on_interval(f, 1, 5)
(-3.28837139559..., 3.4256184695...)
sage: find_minimum_on_interval(f, 1, 5, tol=1e-3)
(-3.28837136189098..., 3.42575079030572...)
sage: find_minimum_on_interval(f, 1, 5, tol=1e-2, maxfun=10)
(-3.28837084598..., 3.4250840220...)
sage: show(plot(f, 0, 20))
sage: find_minimum_on_interval(f, 1, 15)
(-9.4772942594..., 9.5293344109...)
ALGORITHM:
Uses scipy.optimize.fminbound which uses Brent’s method.
AUTHOR:
Numerically find a root of f on the closed interval ![[a,b]](../../_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) (or
(or ![[b,a]](../../_images/math/a5aa84566486814ea5e952727df5d17a1b168480.png) ) if possible, where f is a function in the one variable.
) if possible, where f is a function in the one variable.
INPUT:
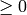 .
The routine modifies this to take into account the relative precision
of doubles.
.
The routine modifies this to take into account the relative precision
of doubles.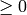 .
.EXAMPLES:
An example involving an algebraic polynomial function:
sage: R.<x> = QQ[]
sage: f = (x+17)*(x-3)*(x-1/8)^3
sage: find_root(f, 0,4)
2.9999999999999951
sage: find_root(f, 0,1) # note -- precision of answer isn't very good on some machines.
0.124999...
sage: find_root(f, -20,-10)
-17.0
In Pomerance book on primes he asserts that the famous Riemann
Hypothesis is equivalent to the statement that the function 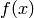 defined below is positive for all
defined below is positive for all 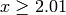 :
:
sage: def f(x):
... return sqrt(x) * log(x) - abs(Li(x) - prime_pi(x))
We find where  equals, i.e., what value that is slightly smaller
than
equals, i.e., what value that is slightly smaller
than 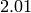 that could have been used in the formulation of the Riemann
Hypothesis:
that could have been used in the formulation of the Riemann
Hypothesis:
sage: find_root(f, 2, 4, rtol=0.0001)
2.0082590205656166
This agrees with the plot:
sage: plot(f,2,2.01)
Solves the dual linear programs:
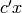 subject to
subject to 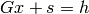 ,
, 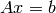 , and
, and 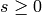 where
where
 denotes transpose.
denotes transpose.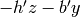 subject to
subject to 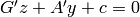 and
and 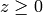 .
.INPUT:
These can be over any field that can be turned into a floating point number.
OUTPUT:
A dictionary sol with keys x, s, y, z corresponding to the variables above:
EXAMPLES:
First, we minimize 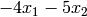 subject to
subject to 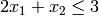 ,
,
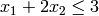 ,
, 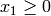 , and
, and 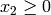 :
:
sage: c=vector(RDF,[-4,-5])
sage: G=matrix(RDF,[[2,1],[1,2],[-1,0],[0,-1]])
sage: h=vector(RDF,[3,3,0,0])
sage: sol=linear_program(c,G,h)
sage: sol['x']
(0.999..., 1.000...)
Next, we maximize 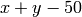 subject to
subject to 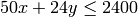 ,
,
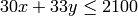 ,
, 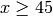 , and
, and 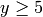 :
:
sage: v=vector([-1.0,-1.0,-1.0])
sage: m=matrix([[50.0,24.0,0.0],[30.0,33.0,0.0],[-1.0,0.0,0.0],[0.0,-1.0,0.0],[0.0,0.0,1.0],[0.0,0.0,-1.0]])
sage: h=vector([2400.0,2100.0,-45.0,-5.0,1.0,-1.0])
sage: sol=linear_program(v,m,h)
sage: sol['x']
(45.000000..., 6.2499999...3, 1.00000000...)
This function is an interface to a variety of algorithms for computing the minimum of a function of several variables.
INPUT:
func – Either a symbolic function or a Python function whose
argument is a tuple with  components
components
x0 – Initial point for finding minimum.
gradient – Optional gradient function. This will be computed automatically for symbolic functions. For Python functions, it allows the use of algorithms requiring derivatives. It should accept a tuple of arguments and return a NumPy array containing the partial derivatives at that point.
hessian – Optional hessian function. This will be computed automatically for symbolic functions. For Python functions, it allows the use of algorithms requiring derivatives. It should accept a tuple of arguments and return a NumPy array containing the second partial derivatives of the function.
algorithm – String specifying algorithm to use. Options are 'default' (for Python functions, the simplex method is the default) (for symbolic functions bfgs is the default):
- 'simplex'
- 'powell'
- 'bfgs' – (broyden-fletcher-goldfarb-shannon) requires gradient
- 'cg' – (conjugate-gradient) requires gradient
- 'ncg' – (newton-conjugate gradient) requires gradient and hessian
EXAMPLES:
sage: vars=var('x y z')
sage: f=100*(y-x^2)^2+(1-x)^2+100*(z-y^2)^2+(1-y)^2
sage: minimize(f,[.1,.3,.4],disp=0)
(1.00..., 1.00..., 1.00...)
sage: minimize(f,[.1,.3,.4],algorithm="ncg",disp=0)
(0.9999999..., 0.999999..., 0.999999...)
Same example with just Python functions:
sage: def rosen(x): # The Rosenbrock function
... return sum(100.0r*(x[1r:]-x[:-1r]**2.0r)**2.0r + (1r-x[:-1r])**2.0r)
sage: minimize(rosen,[.1,.3,.4],disp=0)
(1.00..., 1.00..., 1.00...)
Same example with a pure Python function and a Python function to compute the gradient:
sage: def rosen(x): # The Rosenbrock function
... return sum(100.0r*(x[1r:]-x[:-1r]**2.0r)**2.0r + (1r-x[:-1r])**2.0r)
sage: import numpy
sage: from numpy import zeros
sage: def rosen_der(x):
... xm = x[1r:-1r]
... xm_m1 = x[:-2r]
... xm_p1 = x[2r:]
... der = zeros(x.shape,dtype=float)
... der[1r:-1r] = 200r*(xm-xm_m1**2r) - 400r*(xm_p1 - xm**2r)*xm - 2r*(1r-xm)
... der[0] = -400r*x[0r]*(x[1r]-x[0r]**2r) - 2r*(1r-x[0])
... der[-1] = 200r*(x[-1r]-x[-2r]**2r)
... return der
sage: minimize(rosen,[.1,.3,.4],gradient=rosen_der,algorithm="bfgs",disp=0)
(1.00..., 1.00..., 1.00...)
Minimize a function with constraints.
INPUT:
 components
(assuming
components
(assuming  variables). If the constraints are specified as a list
of intervals and there are no constraints for a given variable, that
component can be (None, None).
variables). If the constraints are specified as a list
of intervals and there are no constraints for a given variable, that
component can be (None, None).EXAMPLES:
Let us maximize 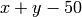 subject to the following constraints:
subject to the following constraints:
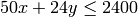 ,
, 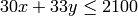 ,
, 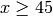 ,
and
,
and 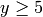 :
:
sage: y = var('y')
sage: f = lambda p: -p[0]-p[1]+50
sage: c_1 = lambda p: p[0]-45
sage: c_2 = lambda p: p[1]-5
sage: c_3 = lambda p: -50*p[0]-24*p[1]+2400
sage: c_4 = lambda p: -30*p[0]-33*p[1]+2100
sage: a = minimize_constrained(f,[c_1,c_2,c_3,c_4],[2,3])
sage: a
(45.0, 6.25)
Let’s find a minimum of 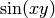 :
:
sage: x,y = var('x y')
sage: f = sin(x*y)
sage: minimize_constrained(f, [(None,None),(4,10)],[5,5])
(4.8..., 4.8...)
Check, if L-BFGS-B finds the same minimum:
sage: minimize_constrained(f, [(None,None),(4,10)],[5,5], algorithm='l-bfgs-b')
(4.7..., 4.9...)
Rosenbrock function, [http://en.wikipedia.org/wiki/Rosenbrock_function]:
sage: from scipy.optimize import rosen, rosen_der
sage: minimize_constrained(rosen, [(-50,-10),(5,10)],[1,1],gradient=rosen_der,algorithm='l-bfgs-b')
(-10.0, 10.0)
sage: minimize_constrained(rosen, [(-50,-10),(5,10)],[1,1],algorithm='l-bfgs-b')
(-10.0, 10.0)
REFERENCES:
| [ZBN97] | C. Zhu, R. H. Byrd and J. Nocedal. L-BFGS-B: Algorithm 778: L-BFGS-B, FORTRAN routines for large scale bound constrained optimization. ACM Transactions on Mathematical Software, Vol 23, Num. 4, pp.550–560, 1997. |