Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Modular Symbols »

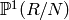 ) over number fields.¶
) over number fields.¶Lists of elements of 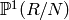 where
where  is the ring of integers of a number
field
is the ring of integers of a number
field  and
and  is an integral ideal.
is an integral ideal.
AUTHORS:
EXAMPLES:
We define a P1NFList:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(5, a^2 - a + 1)
sage: P = P1NFList(N); P
The projective line over the ring of integers modulo the Fractional ideal (5, a^2 - a + 1)
List operations with the P1NFList:
sage: len(P)
26
sage: [p for p in P]
[M-symbol (0: 1) of level Fractional ideal (5, a^2 - a + 1),
...
M-symbol (1: 2*a^2 + 2*a) of level Fractional ideal (5, a^2 - a + 1)]
The elements of the P1NFList are M-symbols:
sage: type(P[2])
<class 'sage.modular.modsym.p1list_nf.MSymbol'>
Definition of MSymbols:
sage: alpha = MSymbol(N, 3, a^2); alpha
M-symbol (3: a^2) of level Fractional ideal (5, a^2 - a + 1)
Find the index of the class of an M-Symbol 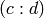 in the list:
in the list:
sage: i = P.index(alpha)
sage: P[i].c*alpha.d - P[i].d*alpha.c in N
True
Lift an MSymbol to a matrix in 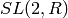 :
:
sage: alpha = MSymbol(N, a + 2, 3*a^2)
sage: alpha.lift_to_sl2_Ok()
[-a - 1, 15*a^2 - 38*a + 86, a + 2, -a^2 + 9*a - 19]
sage: Ok = k.ring_of_integers()
sage: M = Matrix(Ok, 2, alpha.lift_to_sl2_Ok())
sage: det(M)
1
sage: M[1][1] - alpha.d in N
True
Lift an MSymbol from P1NFList to a matrix in 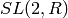
sage: P[3]
M-symbol (1: -2*a) of level Fractional ideal (5, a^2 - a + 1)
sage: P.lift_to_sl2_Ok(3)
[0, -1, 1, -2*a]
Bases: sage.structure.sage_object.SageObject
The constructor for an M-symbol over a number field.
INPUT:
OUTPUT:
An M-symbol modulo the given ideal N, i.e. an element of the
projective line 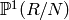 , where R is the ring of integers of
the underlying number field.
, where R is the ring of integers of
the underlying number field.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(a + 1, 2)
sage: MSymbol(N, 3, a^2 + 1)
M-symbol (3: a^2 + 1) of level Fractional ideal (2, a + 1)
We can give a tuple as input:
sage: MSymbol(N, (1, 0))
M-symbol (1: 0) of level Fractional ideal (2, a + 1)
We get an error if <c>, <d> and N are not coprime:
sage: MSymbol(N, 2*a, a - 1)
...
ValueError: (2*a, a - 1) is not an element of P1(R/N).
sage: MSymbol(N, (0, 0))
...
ValueError: (0, 0) is not an element of P1(R/N).
Saving and loading works:
sage: alpha = MSymbol(N, 3, a^2 + 1)
sage: loads(dumps(alpha))==alpha
True
Returns the level or modulus of this MSymbol.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3, a - 1)
sage: alpha = MSymbol(N, 3, a)
sage: alpha.N()
Fractional ideal (3, -1/2*a + 1/2)
Returns the first coefficient of the M-symbol.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(a + 1, 2)
sage: alpha = MSymbol(N, 3, a^2 + 1)
sage: alpha.c # indirect doctest
3
Returns the second coefficient of the M-symbol.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(a + 1, 2)
sage: alpha = MSymbol(N, 3, a^2 + 1)
sage: alpha.d # indirect doctest
a^2 + 1
Lift the MSymbol to an element of 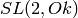 , where
, where 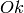 is the ring
of integers of the corresponding number field.
is the ring
of integers of the corresponding number field.
OUTPUT:
A list of integral elements ![[a, b, c', d']](../../../_images/math/62a8fd4975c4ef3dd338ca4643f2bf282c240a87.png) that are the entries of
a 2x2 matrix with determinant 1. The lower two entries are congruent
(modulo the level) to the coefficients
that are the entries of
a 2x2 matrix with determinant 1. The lower two entries are congruent
(modulo the level) to the coefficients 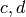 of the MSymbol self.
of the MSymbol self.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3, a - 1)
sage: alpha = MSymbol(N, 3*a + 1, a)
sage: alpha.lift_to_sl2_Ok()
[0, -1, 1, a]
Returns a normalized MSymbol (a canonical representative of an element
of 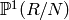 ) equivalent to self.
) equivalent to self.
INPUT:
OUTPUT:
 , such that
, such that
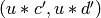 is congruent to
is congruent to 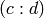 (mod
(mod  ), where
), where 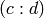 are the coefficients of self and
are the coefficients of self and  is the level.
is the level.EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3, a - 1)
sage: alpha1 = MSymbol(N, 3, a); alpha1
M-symbol (3: a) of level Fractional ideal (3, -1/2*a + 1/2)
sage: alpha1.normalize()
M-symbol (0: 1) of level Fractional ideal (3, -1/2*a + 1/2)
sage: alpha2 = MSymbol(N, 4, a + 1)
sage: alpha2.normalize()
M-symbol (1: -a) of level Fractional ideal (3, -1/2*a + 1/2)
We get the scaling factor by setting with_scalar=True:
sage: alpha1.normalize(with_scalar=True)
(a, M-symbol (0: 1) of level Fractional ideal (3, -1/2*a + 1/2))
sage: r, beta1 = alpha1.normalize(with_scalar=True)
sage: r*beta1.c - alpha1.c in N
True
sage: r*beta1.d - alpha1.d in N
True
sage: r, beta2 = alpha2.normalize(with_scalar=True)
sage: r*beta2.c - alpha2.c in N
True
sage: r*beta2.d - alpha2.d in N
True
Returns the MSymbol as a list (c, d).
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3, a - 1)
sage: alpha = MSymbol(N, 3, a); alpha
M-symbol (3: a) of level Fractional ideal (3, -1/2*a + 1/2)
sage: alpha.tuple()
(3, a)
Bases: sage.structure.sage_object.SageObject
The class for 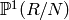 , the projective line modulo
, the projective line modulo  , where
, where
 is the ring of integers of a number field
is the ring of integers of a number field  and
and  is an integral ideal.
is an integral ideal.
INPUT:
OUTPUT:
A P1NFList object representing 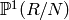 .
.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(5, a + 1)
sage: P = P1NFList(N); P
The projective line over the ring of integers modulo the Fractional ideal (5, a + 1)
Saving and loading works.
sage: loads(dumps(P)) == P
True
Returns the level or modulus of this P1NFList.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 31)
sage: N = k.ideal(5, a + 3)
sage: P = P1NFList(N)
sage: P.N()
Fractional ideal (5, a + 3)
Applies the matrix 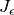 = [e1, 0, 0, e2] to the i-th
M-Symbol of the list.
= [e1, 0, 0, e2] to the i-th
M-Symbol of the list.
e1, e2 are units of the underlying number field.
INPUT:
OUTPUT:
integer – the index of the M-Symbol obtained by the right action of
the matrix 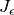 = [e1, 0, 0, e2] on the i-th M-Symbol.
= [e1, 0, 0, e2] on the i-th M-Symbol.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(5, a + 1)
sage: P = P1NFList(N)
sage: u = k.unit_group().gens(); u
[-1, 2*a^2 + 4*a - 1]
sage: P.apply_J_epsilon(4, -1)
2
sage: P.apply_J_epsilon(4, u[0], u[1])
1
sage: k.<a> = NumberField(x^4 + 13*x - 7)
sage: N = k.ideal(a + 1)
sage: P = P1NFList(N)
sage: u = k.unit_group().gens(); u
[-1, a^3 + a^2 + a + 12, a^3 + 3*a^2 - 1]
sage: P.apply_J_epsilon(3, u[2]^2)==P.apply_J_epsilon(P.apply_J_epsilon(3, u[2]),u[2])
True
Applies the matrix S = [0, -1, 1, 0] to the i-th M-Symbol of the list.
INPUT:
OUTPUT:
integer – the index of the M-Symbol obtained by the right action of the matrix S = [0, -1, 1, 0] on the i-th M-Symbol.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(5, a + 1)
sage: P = P1NFList(N)
sage: j = P.apply_S(P.index_of_normalized_pair(1, 0))
sage: P[j]
M-symbol (0: 1) of level Fractional ideal (5, a + 1)
We test that S has order 2:
sage: j = randint(0,len(P)-1)
sage: P.apply_S(P.apply_S(j))==j
True
Applies the matrix TS = [1, -1, 0, 1] to the i-th M-Symbol of the list.
INPUT:
OUTPUT:
integer – the index of the M-Symbol obtained by the right action of the matrix TS = [1, -1, 0, 1] on the i-th M-Symbol.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(5, a + 1)
sage: P = P1NFList(N)
sage: P.apply_TS(3)
2
We test that TS has order 3:
sage: j = randint(0,len(P)-1)
sage: P.apply_TS(P.apply_TS(P.apply_TS(j)))==j
True
Applies the matrix T_alpha = [1, alpha, 0, 1] to the i-th M-Symbol of the list.
INPUT:
OUTPUT:
integer – the index of the M-Symbol obtained by the right action of the matrix T_alpha = [1, alpha, 0, 1] on the i-th M-Symbol.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(5, a + 1)
sage: P = P1NFList(N)
sage: P.apply_T_alpha(4, a^ 2 - 2)
3
We test that T_a*T_b = T_(a+b):
sage: P.apply_T_alpha(3, a^2 - 2)==P.apply_T_alpha(P.apply_T_alpha(3,a^2),-2)
True
Returns the index of the class of the pair 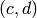 in the fixed list
of representatives of
in the fixed list
of representatives of 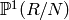 .
.
INPUT:
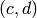 defines an M-symbol of level
defines an M-symbol of level  .
.OUTPUT:
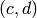 in the list.
in the list.EXAMPLES:
sage: k.<a> = NumberField(x^2 + 31)
sage: N = k.ideal(5, a + 3)
sage: P = P1NFList(N)
sage: P.index(3,a)
5
sage: P[5]==MSymbol(N, 3, a).normalize()
True
We can give an MSymbol as input:
sage: alpha = MSymbol(N, 3, a)
sage: P.index(alpha)
5
We cannot look for the class of an MSymbol of a different level:
sage: M = k.ideal(a + 1)
sage: beta = MSymbol(M, 0, 1)
sage: P.index(beta)
...
ValueError: The MSymbol is of a different level
If we are interested in the transforming scalar:
sage: alpha = MSymbol(N, 3, a)
sage: P.index(alpha, with_scalar=True)
(-a, 5)
sage: u, i = P.index(alpha, with_scalar=True)
sage: (u*P[i].c - alpha.c in N) and (u*P[i].d - alpha.d in N)
True
Returns the index of the class 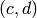 in the fixed list of
representatives of
in the fixed list of
representatives of 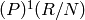 .
.
INPUT:
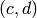 defines a normalized M-symbol of
level
defines a normalized M-symbol of
level  .
.OUTPUT:
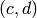 in the list.
in the list.EXAMPLES:
sage: k.<a> = NumberField(x^2 + 31)
sage: N = k.ideal(5, a + 3)
sage: P = P1NFList(N)
sage: P.index_of_normalized_pair(1, 0)
3
sage: j = randint(0,len(P)-1)
sage: P.index_of_normalized_pair(P[j])==j
True
Lift the  -th element of this P1NFList to an element of
-th element of this P1NFList to an element of 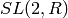 ,
where
,
where  is the ring of integers of the corresponding number field.
is the ring of integers of the corresponding number field.
INPUT:
OUTPUT:
If the  -th element is
-th element is 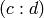 , the function returns a list of
integral elements
, the function returns a list of
integral elements ![[a, b, c', d']](../../../_images/math/62a8fd4975c4ef3dd338ca4643f2bf282c240a87.png) that defines a 2x2 matrix with
determinant 1 and such that
that defines a 2x2 matrix with
determinant 1 and such that 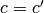 (mod
(mod  ) and
) and 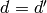 (mod
(mod  ).
).
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3)
sage: P = P1NFList(N)
sage: len(P)
16
sage: P[5]
M-symbol (1/2*a + 1/2: -a) of level Fractional ideal (3)
sage: P.lift_to_sl2_Ok(5)
[1, -2, 1/2*a + 1/2, -a]
sage: Ok = k.ring_of_integers()
sage: L = [Matrix(Ok, 2, P.lift_to_sl2_Ok(i)) for i in range(len(P))]
sage: all([det(L[i]) == 1 for i in range(len(L))])
True
Returns the underlying list of this P1NFList object.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(5, a+1)
sage: P = P1NFList(N)
sage: type(P)
<class 'sage.modular.modsym.p1list_nf.P1NFList'>
sage: type(P.list())
<type 'list'>
Returns a normalised element of 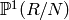 .
.
INPUT:
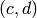 defines an M-symbol of level
defines an M-symbol of level  .
.OUTPUT:
 , such that
, such that
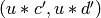 is congruent to
is congruent to 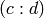 (mod
(mod  ).
).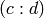 .
.EXAMPLES:
sage: k.<a> = NumberField(x^2 + 31)
sage: N = k.ideal(5, a + 3)
sage: P = P1NFList(N)
sage: P.normalize(3, a)
M-symbol (1: 2*a) of level Fractional ideal (5, a + 3)
We can use an MSymbol as input:
sage: alpha = MSymbol(N, 3, a)
sage: P.normalize(alpha)
M-symbol (1: 2*a) of level Fractional ideal (5, a + 3)
If we are interested in the normalizing scalar:
sage: P.normalize(alpha, with_scalar=True)
(-a, M-symbol (1: 2*a) of level Fractional ideal (5, a + 3))
sage: r, beta = P.normalize(alpha, with_scalar=True)
sage: (r*beta.c - alpha.c in N) and (r*beta.d - alpha.d in N)
True
Clear the global cache of data for the level ideals.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: N = k.ideal(a+1)
sage: alpha = MSymbol(N, 2*a^2, 5)
sage: alpha.normalize()
M-symbol (-4*a^2: 5*a^2) of level Fractional ideal (a + 1)
sage: sage.modular.modsym.p1list_nf._level_cache
{Fractional ideal (a + 1): (...)}
sage: sage.modular.modsym.p1list_nf.P1NFList_clear_level_cache()
sage: sage.modular.modsym.p1list_nf._level_cache
{}
Lift a pair (c, d) to an element of 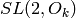 , where
, where 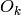 is the ring
of integers of the corresponding number field.
is the ring
of integers of the corresponding number field.
INPUT:
OUTPUT:
A list [a, b, c’, d’] of integral elements that are the entries of
a 2x2 matrix with determinant 1. The lower two entries are congruent to
c, d modulo the ideal  .
.
EXAMPLES:
sage: from sage.modular.modsym.p1list_nf import lift_to_sl2_Ok
sage: k.<a> = NumberField(x^2 + 23)
sage: Ok = k.ring_of_integers(k)
sage: N = k.ideal(3)
sage: M = Matrix(Ok, 2, lift_to_sl2_Ok(N, 1, a))
sage: det(M)
1
sage: M = Matrix(Ok, 2, lift_to_sl2_Ok(N, 0, a))
sage: det(M)
1
sage: (M[1][0] in N) and (M[1][1] - a in N)
True
sage: M = Matrix(Ok, 2, lift_to_sl2_Ok(N, 0, 0))
...
ValueError: Cannot lift (0, 0) to an element of Sl2(Ok).
sage: k.<a> = NumberField(x^3 + 11)
sage: Ok = k.ring_of_integers(k)
sage: N = k.ideal(3, a - 1)
sage: M = Matrix(Ok, 2, lift_to_sl2_Ok(N, 2*a, 0))
sage: det(M)
1
sage: (M[1][0] - 2*a in N) and (M[1][1] in N)
True
sage: M = Matrix(Ok, 2, lift_to_sl2_Ok(N, 4*a^2, a + 1))
sage: det(M)
1
sage: (M[1][0] - 4*a^2 in N) and (M[1][1] - (a+1) in N)
True
sage: k.<a> = NumberField(x^4 - x^3 -21*x^2 + 17*x + 133)
sage: Ok = k.ring_of_integers(k)
sage: N = k.ideal(7, a)
sage: M = Matrix(Ok, 2, lift_to_sl2_Ok(N, 0, a^2 - 1))
sage: det(M)
1
sage: (M[1][0] in N) and (M[1][1] - (a^2-1) in N)
True
sage: M = Matrix(Ok, 2, lift_to_sl2_Ok(N, 0, 7))
...
ValueError: <0> + <7> and the Fractional ideal (7, a) are not coprime.
Returns (c, d’) so d’ is congruent to d modulo N, and such that c and d’ are coprime (<c> + <d’> = R).
INPUT:
OUTPUT:
A pair (c, d’) where c, d’ are integral elements of the corresponding number field, with d’ congruent to d mod N, and such that <c> + <d’> = R (R being the corresponding ring of integers).
EXAMPLES:
sage: from sage.modular.modsym.p1list_nf import make_coprime
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3, a - 1)
sage: c = 2*a; d = a + 1
sage: N.is_coprime(k.ideal(c, d))
True
sage: k.ideal(c).is_coprime(d)
False
sage: c, dp = make_coprime(N, c, d)
sage: k.ideal(c).is_coprime(dp)
True
Returns a list of the normalized elements of 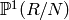 , where
, where
 is an integral ideal.
is an integral ideal.
INPUT:
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3)
sage: from sage.modular.modsym.p1list_nf import p1NFlist, psi
sage: len(p1NFlist(N))==psi(N)
True
The index ![[\Gamma : \Gamma_0(N)]](../../../_images/math/3e336e2fa972e572f6a36ed46d1d6aafa7938f43.png) , where
, where 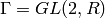 for
for  the
corresponding ring of integers, and
the
corresponding ring of integers, and 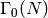 standard congruence
subgroup.
standard congruence
subgroup.
EXAMPLES:
sage: from sage.modular.modsym.p1list_nf import psi
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3, a - 1)
sage: psi(N)
4
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(5)
sage: psi(N)
26