Eisenstein Series

sage.modular.modform.eis_series.compute_eisenstein_params(character, k)

Compute and return a list of all parameters 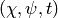that define the Eisenstein series with given character and weight .

Only the parity of is relevant (unless k = 1, which is a slightly different case).

If character is an integer , then the parameters for 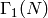are computed instead. Then the condition is that .

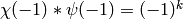EXAMPLES:

sage: sage.modular.modform.eis_series.compute_eisenstein_params(DirichletGroup(30)(1), 3)
[]

sage: pars =  sage.modular.modform.eis_series.compute_eisenstein_params(DirichletGroup(30)(1), 4)
sage: [(x[0].values_on_gens(), x[1].values_on_gens(), x[2]) for x in pars]
[((1, 1), (1, 1), 1),
((1, 1), (1, 1), 2),
((1, 1), (1, 1), 3),
((1, 1), (1, 1), 5),
((1, 1), (1, 1), 6),
((1, 1), (1, 1), 10),
((1, 1), (1, 1), 15),
((1, 1), (1, 1), 30)]

sage: pars = sage.modular.modform.eis_series.compute_eisenstein_params(15, 1)
sage: [(x[0].values_on_gens(), x[1].values_on_gens(), x[2]) for x in pars]
[((1, 1), (-1, 1), 1),
((1, 1), (-1, 1), 5), 
((1, 1), (1, zeta4), 1),
((1, 1), (1, zeta4), 3),
((1, 1), (-1, -1), 1),
((1, 1), (1, -zeta4), 1),
((1, 1), (1, -zeta4), 3),
((-1, 1), (1, -1), 1)]

sage: sage.modular.modform.eis_series.compute_eisenstein_params(DirichletGroup(15).0, 1)
[(Dirichlet character modulo 15 of conductor 1 mapping 11 |--> 1, 7 |--> 1, Dirichlet character modulo 15 of conductor 3 mapping 11 |--> -1, 7 |--> 1, 1),
(Dirichlet character modulo 15 of conductor 1 mapping 11 |--> 1, 7 |--> 1, Dirichlet character modulo 15 of conductor 3 mapping 11 |--> -1, 7 |--> 1, 5)]

sage.modular.modform.eis_series.eisenstein_series_lseries(weight, prec=53, max_imaginary_part=0, max_asymp_coeffs=40)

Return the L-series of the weight 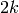Eisenstein series on .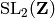

This actually returns an interface to Tim Dokchitser’s program for computing with the L-series of the Eisenstein series

INPUT:

• weight - even integer
• prec - integer (bits precision)
• max_imaginary_part - real number
• max_asymp_coeffs - integer

OUTPUT:

The L-series of the Eisenstein series.

EXAMPLES:

We compute with the L-series of 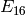and then :

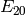sage: L = eisenstein_series_lseries(16)
sage: L(1)
-0.291657724743873
sage: L = eisenstein_series_lseries(20)
sage: L(2)
-5.02355351645987 

sage.modular.modform.eis_series.eisenstein_series_qexp(k, prec=10, K=Rational Field, var='q')

Return the -expansion of the normalized weight Eisenstein series on 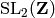to precision prec in the ring . (The normalization chosen here is the one that forces the coefficient of to be 1.)

INPUT:

• k - an even positive integer
• prec - (default: 10) a nonnegative integer
• K - (default: ) a ring in which the denominator of 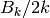is invertible
• var - (default: ‘q’) variable name to use for q-expansion

ALGORITHM:

We know . So we compute all the simultaneously, using the fact that is multiplicative.

EXAMPLES:

sage: eisenstein_series_qexp(2,5)
-1/24 + q + 3*q^2 + 4*q^3 + 7*q^4 + O(q^5)
sage: eisenstein_series_qexp(2,0)
O(q^0)
sage: eisenstein_series_qexp(2,5,GF(7))
2 + q + 3*q^2 + 4*q^3 + O(q^5)
sage: eisenstein_series_qexp(2,5,GF(7),var='T')
2 + T + 3*T^2 + 4*T^3 + O(T^5)

sage: eisenstein_series_qexp(10, 30, GF(17))
15 + q + 3*q^2 + 15*q^3 + 7*q^4 + 13*q^5 + 11*q^6 + 11*q^7 + 15*q^8 + 7*q^9 + 5*q^10 + 7*q^11 + 3*q^12 + 14*q^13 + 16*q^14 + 8*q^15 + 14*q^16 + q^17 + 4*q^18 + 3*q^19 + 6*q^20 + 12*q^21 + 4*q^22 + 12*q^23 + 4*q^24 + 4*q^25 + 8*q^26 + 14*q^27 + 9*q^28 + 6*q^29 + O(q^30)

AUTHORS:

• William Stein: original implementation
• Craig Citro (2007-06-01): rewrote for massive speedup
• Martin Raum (2009-08-02): port to cython for speedup
• David Loeffler (2010-04-07): work around an integer overflow when k is large