Creating Spaces of Modular Forms¶

EXAMPLES:

sage: m = ModularForms(Gamma1(4),11)
sage: m
Modular Forms space of dimension 6 for Congruence Subgroup Gamma1(4) of weight 11 over Rational Field
sage: m.basis()
[
q - 134*q^5 + O(q^6),
q^2 + 80*q^5 + O(q^6),
q^3 + 16*q^5 + O(q^6),
q^4 - 4*q^5 + O(q^6),
1 + 4092/50521*q^2 + 472384/50521*q^3 + 4194300/50521*q^4 + O(q^6),
q + 1024*q^2 + 59048*q^3 + 1048576*q^4 + 9765626*q^5 + O(q^6)
]

sage.modular.modform.constructor.CuspForms(group=1, weight=2, base_ring=None, use_cache=True, prec=6)¶

Create a space of cuspidal modular forms.

See the documentation for the ModularForms command for a description of the input parameters.

EXAMPLES:

sage: CuspForms(11,2)
Cuspidal subspace of dimension 1 of Modular Forms space of dimension 2 for Congruence Subgroup Gamma0(11) of weight 2 over Rational Field

sage.modular.modform.constructor.EisensteinForms(group=1, weight=2, base_ring=None, use_cache=True, prec=6)¶

Create a space of eisenstein modular forms.

See the documentation for the ModularForms command for a description of the input parameters.

EXAMPLES:

sage: EisensteinForms(11,2)
Eisenstein subspace of dimension 1 of Modular Forms space of dimension 2 for Congruence Subgroup Gamma0(11) of weight 2 over Rational Field

sage.modular.modform.constructor.ModularForms(group=1, weight=2, base_ring=None, use_cache=True, prec=6)¶

Create an ambient space of modular forms.

INPUT:

group - A congruence subgroup or a Dirichlet character eps.
weight - int, the weight, which must be an integer = 1.
base_ring - the base ring (ignored if group is a Dirichlet character)

Create using the command ModularForms(group, weight, base_ring) where group could be either a congruence subgroup or a Dirichlet character.

EXAMPLES: First we create some spaces with trivial character:

sage: ModularForms(Gamma0(11),2).dimension()
2
sage: ModularForms(Gamma0(1),12).dimension()
2

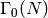If we give an integer N for the congruence subgroup, it defaults to $\Gamma_0(N)$ :

sage: ModularForms(1,12).dimension()
2
sage: ModularForms(11,4)
Modular Forms space of dimension 4 for Congruence Subgroup Gamma0(11) of weight 4 over Rational Field

We create some spaces for 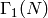$\Gamma_1(N)$ .

sage: ModularForms(Gamma1(13),2)
Modular Forms space of dimension 13 for Congruence Subgroup Gamma1(13) of weight 2 over Rational Field
sage: ModularForms(Gamma1(13),2).dimension()
13
sage: [ModularForms(Gamma1(7),k).dimension() for k in [2,3,4,5]]
[5, 7, 9, 11]
sage: ModularForms(Gamma1(5),11).dimension()
12

We create a space with character:

sage: e = (DirichletGroup(13).0)^2
sage: e.order()
6
sage: M = ModularForms(e, 2); M
Modular Forms space of dimension 3, character [zeta6] and weight 2 over Cyclotomic Field of order 6 and degree 2
sage: f = M.T(2).charpoly('x'); f
x^3 + (-2*zeta6 - 2)*x^2 - 2*zeta6*x + 14*zeta6 - 7
sage: f.factor()
(x - 2*zeta6 - 1) * (x - zeta6 - 2) * (x + zeta6 + 1)

More examples of spaces with character:

sage: e = DirichletGroup(5, RationalField()).gen(); e
Dirichlet character modulo 5 of conductor 5 mapping 2 |--> -1

sage: m = ModularForms(e, 2); m
Modular Forms space of dimension 2, character [-1] and weight 2 over Rational Field
sage: m == loads(dumps(m))
True
sage: m.T(2).charpoly('x')
x^2 - 1
sage: m = ModularForms(e, 6); m.dimension()
4
sage: m.T(2).charpoly('x')
x^4 - 917*x^2 - 42284

This came up in a subtle bug (trac #5923):

sage: ModularForms(gp(1), gap(12))
Modular Forms space of dimension 2 for Modular Group SL(2,Z) of weight 12 over Rational Field

This came up in another bug (related to trac #8630):

sage: chi = DirichletGroup(109, CyclotomicField(3)).0
sage: ModularForms(chi, 2, base_ring = CyclotomicField(15))
Modular Forms space of dimension 10, character [zeta3 + 1] and weight 2 over Cyclotomic Field of order 15 and degree 8

We create some weight 1 spaces. The first example works fine, since we can prove purely by Riemann surface theory that there are no weight 1 cusp forms:

sage: M = ModularForms(Gamma1(11), 1); M
Modular Forms space of dimension 5 for Congruence Subgroup Gamma1(11) of weight 1 over Rational Field
sage: M.basis()
[                                                                                           
1 + 22*q^5 + O(q^6),                                                                        
q + 4*q^5 + O(q^6),                                                                         
q^2 - 4*q^5 + O(q^6),                                                                       
q^3 - 5*q^5 + O(q^6),                                                                       
q^4 - 3*q^5 + O(q^6)                                                                        
]                                                                                           
sage: M.cuspidal_subspace().basis()
[
]
sage: M == M.eisenstein_subspace()
True

This example doesn’t work so well, because we can’t calculate the cusp forms; but we can still work with the Eisenstein series.

sage: M = ModularForms(Gamma1(57), 1); M Modular Forms space of dimension (unknown) for Congruence Subgroup Gamma1(57) of weight 1 over Rational Field sage: M.basis() Traceback (most recent call last): ... NotImplementedError: Computation of dimensions of weight 1 cusp forms spaces not implemented in general sage: M.cuspidal_subspace().basis() Traceback (most recent call last): ... NotImplementedError: Computation of dimensions of weight 1 cusp forms spaces not implemented in general

sage: E = M.eisenstein_subspace(); E Eisenstein subspace of dimension 36 of Modular Forms space of dimension (unknown) for Congruence Subgroup Gamma1(57) of weight 1 over Rational Field sage: (E.0 + E.2).q_expansion(40) 1 + q^2 + 1473/2*q^36 - 1101/2*q^37 + q^38 - 373/2*q^39 + O(q^40)

sage.modular.modform.constructor.ModularForms_clear_cache()¶

Clear the cache of modular forms.

EXAMPLES:

sage: M = ModularForms(37,2)
sage: sage.modular.modform.constructor._cache == {}
False

sage: sage.modular.modform.constructor.ModularForms_clear_cache()
sage: sage.modular.modform.constructor._cache  
{}

sage.modular.modform.constructor.Newform(identifier, group=None, weight=2, base_ring=Rational Field, names=None)¶

INPUT:

identifier - a canonical label, or the index of the specific newform desired
group - the congruence subgroup of the newform
weight - the weight of the newform (default 2)
base_ring - the base ring
names - if the newform has coefficients in a number field, a generator name must be specified

EXAMPLES:

sage: Newform('67a', names='a')
q + 2*q^2 - 2*q^3 + 2*q^4 + 2*q^5 + O(q^6)
sage: Newform('67b', names='a')
q + a1*q^2 + (-a1 - 3)*q^3 + (-3*a1 - 3)*q^4 - 3*q^5 + O(q^6)

sage.modular.modform.constructor.Newforms(group, weight=2, base_ring=None, names=None)¶

Returns a list of the newforms of the given weight and level (or weight, level and character). These are calculated as 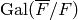$\operatorname{Gal}(\overline{F} / F)$ -orbits, where 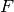$F$ is the given base field.

INPUT:

group - the congruence subgroup of the newform, or a Nebentypus character
weight - the weight of the newform (default 2)
base_ring - the base ring (defaults to $\QQ$ for spaces without character, or the base ring of the character otherwise)
names - if the newform has coefficients in a number field, a generator name must be specified

EXAMPLES:

sage: Newforms(11, 2)
[q - 2*q^2 - q^3 + 2*q^4 + q^5 + O(q^6)]
sage: Newforms(65, names='a')
[q - q^2 - 2*q^3 - q^4 - q^5 + O(q^6),
 q + a1*q^2 + (a1 + 1)*q^3 + (-2*a1 - 1)*q^4 + q^5 + O(q^6),
 q + a2*q^2 + (-a2 + 1)*q^3 + q^4 - q^5 + O(q^6)]

A more complicated example involving both a nontrivial character, and a base field that is not minimal for that character:

sage: K.<i> = QuadraticField(-1)
sage: chi = DirichletGroup(5, K).gen(0)
sage: len(Newforms(chi, 7, names='a'))
1
sage: x = polygen(K); L.<c> = K.extension(x^2 - 402*i)
sage: N = Newforms(chi, 7, base_ring = L); len(N)
2
sage: sorted([N[0][2], N[1][2]]) == sorted([1/2*c - 5/2*i - 5/2, -1/2*c - 5/2*i - 5/2])
True

We test that #8630 is fixed:

sage: chi = DirichletGroup(109, CyclotomicField(3)).0
sage: CuspForms(chi, 2, base_ring = CyclotomicField(9))
Cuspidal subspace of dimension 8 of Modular Forms space of dimension 10, character [zeta3 + 1] and weight 2 over Cyclotomic Field of order 9 and degree 6

sage.modular.modform.constructor.canonical_parameters(group, level, weight, base_ring)¶

Given a group, level, weight, and base_ring as input by the user, return a canonicalized version of them, where level is a Sage integer, group really is a group, weight is a Sage integer, and base_ring a Sage ring. Note that we can’t just get the level from the group, because we have the convention that the character for Gamma1(N) is None (which makes good sense).

INPUT:

group - int, long, Sage integer, group, dirichlet character, or
level - int, long, Sage integer, or group
weight - coercible to Sage integer
base_ring - commutative Sage ring

OUTPUT:

level - Sage integer
group - congruence subgroup
weight - Sage integer
ring - commutative Sage ring

EXAMPLES:

sage: from sage.modular.modform.constructor import canonical_parameters
sage: v = canonical_parameters(5, 5, int(7), ZZ); v
(5, Congruence Subgroup Gamma0(5), 7, Integer Ring)
sage: type(v[0]), type(v[1]), type(v[2]), type(v[3])
(<type 'sage.rings.integer.Integer'>,
 <class 'sage.modular.arithgroup.congroup_gamma0.Gamma0_class'>,
 <type 'sage.rings.integer.Integer'>,
 <type 'sage.rings.integer_ring.IntegerRing_class'>)
sage: canonical_parameters( 5, 7, 7, ZZ )
...
ValueError: group and level do not match.

sage.modular.modform.constructor.parse_label(s)¶

Given a string s corresponding to a newform label, return the corresponding group and index.

EXAMPLES:

sage: sage.modular.modform.constructor.parse_label('11a')
(Congruence Subgroup Gamma0(11), 0)
sage: sage.modular.modform.constructor.parse_label('11aG1')
(Congruence Subgroup Gamma1(11), 0)        
sage: sage.modular.modform.constructor.parse_label('11wG1')
(Congruence Subgroup Gamma1(11), 22)

Creating Spaces of Modular Forms¶

Previous topic

Next topic

This Page

Navigation

Creating Spaces of Modular Forms¶

Previous topic

Next topic

This Page

Quick search

Navigation