Modular Forms 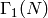for over .

EXAMPLES:

sage: M = ModularForms(Gamma1(13),2); M
Modular Forms space of dimension 13 for Congruence Subgroup Gamma1(13) of weight 2 over Rational Field
sage: S = M.cuspidal_submodule(); S
Cuspidal subspace of dimension 2 of Modular Forms space of dimension 13 for Congruence Subgroup Gamma1(13) of weight 2 over Rational Field
sage: S.basis()
[
q - 4*q^3 - q^4 + 3*q^5 + O(q^6),
q^2 - 2*q^3 - q^4 + 2*q^5 + O(q^6)
]

TESTS:

sage: m = ModularForms(Gamma1(20),2)
sage: loads(dumps(m)) == m
True

class sage.modular.modform.ambient_g1.ModularFormsAmbient_g1_Q(level, weight)

Bases: sage.modular.modform.ambient.ModularFormsAmbient

A space of modular forms for the group 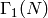over the rational numbers.

cuspidal_submodule()

Return the cuspidal submodule of this modular forms space.

EXAMPLES:

sage: m = ModularForms(Gamma1(17),2); m
Modular Forms space of dimension 20 for Congruence Subgroup Gamma1(17) of weight 2 over Rational Field
sage: m.cuspidal_submodule()
Cuspidal subspace of dimension 5 of Modular Forms space of dimension 20 for Congruence Subgroup Gamma1(17) of weight 2 over Rational Field

eisenstein_submodule()

Return the Eisenstein submodule of this modular forms space.

EXAMPLES:

sage: ModularForms(Gamma1(13),2).eisenstein_submodule()
Eisenstein subspace of dimension 11 of Modular Forms space of dimension 13 for Congruence Subgroup Gamma1(13) of weight 2 over Rational Field
sage: ModularForms(Gamma1(13),10).eisenstein_submodule()
Eisenstein subspace of dimension 12 of Modular Forms space of dimension 69 for Congruence Subgroup Gamma1(13) of weight 10 over Rational Field