Sage can compute with Hecke operators on modular abelian varieties. A Hecke operator is defined by given a modular abelian variety and an index. Given a Hecke operator, Sage can compute the characteristic polynomial, and the action of the Hecke operator on various homology groups.
AUTHORS:
EXAMPLES:
sage: A = J0(54)
sage: t5 = A.hecke_operator(5); t5
Hecke operator T_5 on Abelian variety J0(54) of dimension 4
sage: t5.charpoly().factor()
(x - 3) * (x + 3) * x^2
sage: B = A.new_subvariety(); B
Abelian subvariety of dimension 2 of J0(54)
sage: t5 = B.hecke_operator(5); t5
Hecke operator T_5 on Abelian subvariety of dimension 2 of J0(54)
sage: t5.charpoly().factor()
(x - 3) * (x + 3)
sage: t5.action_on_homology().matrix()
[ 0 3 3 -3]
[-3 3 3 0]
[ 3 3 0 -3]
[-3 6 3 -3]
Bases: sage.modular.abvar.morphism.Morphism
Return the list of indices defining self.
EXAMPLES:
sage: J0(22).degeneracy_map(44).t()
[1]
sage: J = J0(22) * J0(11)
sage: J.degeneracy_map([44,44], [2,1])
Degeneracy map from Abelian variety J0(22) x J0(11) of dimension 3 to Abelian variety J0(44) x J0(44) of dimension 8 defined by [2, 1]
sage: J.degeneracy_map([44,44], [2,1]).t()
[2, 1]
Bases: sage.modular.abvar.morphism.Morphism
A Hecke operator acting on a modular abelian variety.
Return the action of this Hecke operator on the homology
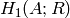 of this abelian variety with coefficients in
of this abelian variety with coefficients in
 .
.
EXAMPLES:
sage: A = J0(43)
sage: t2 = A.hecke_operator(2); t2
Hecke operator T_2 on Abelian variety J0(43) of dimension 3
sage: h2 = t2.action_on_homology(); h2
Hecke operator T_2 on Integral Homology of Abelian variety J0(43) of dimension 3
sage: h2.matrix()
[-2 1 0 0 0 0]
[-1 1 1 0 -1 0]
[-1 0 -1 2 -1 1]
[-1 0 1 1 -1 1]
[ 0 -2 0 2 -2 1]
[ 0 -1 0 1 0 -1]
sage: h2 = t2.action_on_homology(GF(2)); h2
Hecke operator T_2 on Homology with coefficients in Finite Field of size 2 of Abelian variety J0(43) of dimension 3
sage: h2.matrix()
[0 1 0 0 0 0]
[1 1 1 0 1 0]
[1 0 1 0 1 1]
[1 0 1 1 1 1]
[0 0 0 0 0 1]
[0 1 0 1 0 1]
Return the characteristic polynomial of this Hecke operator in the given variable.
INPUT:
OUTPUT: a polynomial in var over the rational numbers.
EXAMPLES:
sage: A = J0(43)[1]; A
Simple abelian subvariety 43b(1,43) of dimension 2 of J0(43)
sage: t2 = A.hecke_operator(2); t2
Hecke operator T_2 on Simple abelian subvariety 43b(1,43) of dimension 2 of J0(43)
sage: f = t2.characteristic_polynomial(); f
x^2 - 2
sage: f.parent()
Univariate Polynomial Ring in x over Integer Ring
sage: f.factor()
x^2 - 2
sage: t2.characteristic_polynomial('y')
y^2 - 2
Synonym for self.characteristic_polynomial(var).
INPUT:
EXAMPLES:
sage: A = J1(13)
sage: t2 = A.hecke_operator(2); t2
Hecke operator T_2 on Abelian variety J1(13) of dimension 2
sage: f = t2.charpoly(); f
x^2 + 3*x + 3
sage: f.factor()
x^2 + 3*x + 3
sage: t2.charpoly('y')
y^2 + 3*y + 3
Return the index of this Hecke operator. (For example, if this is
the operator 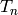 , then the index is the integer
, then the index is the integer
 .)
.)
OUTPUT:
EXAMPLES:
sage: J = J0(15)
sage: t = J.hecke_operator(53)
sage: t
Hecke operator T_53 on Abelian variety J0(15) of dimension 1
sage: t.index()
53
sage: t = J.hecke_operator(54)
sage: t
Hecke operator T_54 on Abelian variety J0(15) of dimension 1
sage: t.index()
54
sage: J = J1(12345)
sage: t = J.hecke_operator(997) ; t
Hecke operator T_997 on Abelian variety J1(12345) of dimension 5405473
sage: t.index()
997
sage: type(t.index())
<type 'sage.rings.integer.Integer'>
Return the matrix of self acting on the homology
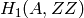 of this abelian variety with coefficients in
of this abelian variety with coefficients in
 .
.
EXAMPLES:
sage: J0(47).hecke_operator(3).matrix()
[ 0 0 1 -2 1 0 -1 0]
[ 0 0 1 0 -1 0 0 0]
[-1 2 0 0 2 -2 1 -1]
[-2 1 1 -1 3 -1 -1 0]
[-1 -1 1 0 1 0 -1 1]
[-1 0 0 -1 2 0 -1 0]
[-1 -1 2 -2 2 0 -1 0]
[ 0 -1 0 0 1 0 -1 1]
sage: J0(11).hecke_operator(7).matrix()
[-2 0]
[ 0 -2]
sage: (J0(11) * J0(33)).hecke_operator(7).matrix()
[-2 0 0 0 0 0 0 0]
[ 0 -2 0 0 0 0 0 0]
[ 0 0 0 0 2 -2 2 -2]
[ 0 0 0 -2 2 0 2 -2]
[ 0 0 0 0 2 0 4 -4]
[ 0 0 -4 0 2 2 2 -2]
[ 0 0 -2 0 2 2 0 -2]
[ 0 0 -2 0 0 2 0 -2]
sage: J0(23).hecke_operator(2).matrix()
[ 0 1 -1 0]
[ 0 1 -1 1]
[-1 2 -2 1]
[-1 1 0 -1]
Alias for self.index().
EXAMPLES:
sage: J = J0(17)
sage: J.hecke_operator(5).n()
5
Bases: sage.modular.abvar.morphism.Morphism_abstract, sage.modules.matrix_morphism.MatrixMorphism
Restrict self to the subvariety sub of self.domain().
EXAMPLES:
sage: J = J0(37) ; A, B = J.decomposition()
sage: A.lattice().matrix()
[ 1 -1 1 0]
[ 0 0 2 -1]
sage: B.lattice().matrix()
[1 1 1 0]
[0 0 0 1]
sage: T = J.hecke_operator(2) ; T.matrix()
[-1 1 1 -1]
[ 1 -1 1 0]
[ 0 0 -2 1]
[ 0 0 0 0]
sage: T.restrict_domain(A)
Abelian variety morphism:
From: Simple abelian subvariety 37a(1,37) of dimension 1 of J0(37)
To: Abelian variety J0(37) of dimension 2
sage: T.restrict_domain(A).matrix()
[-2 2 -2 0]
[ 0 0 -4 2]
sage: T.restrict_domain(B)
Abelian variety morphism:
From: Simple abelian subvariety 37b(1,37) of dimension 1 of J0(37)
To: Abelian variety J0(37) of dimension 2
sage: T.restrict_domain(B).matrix()
[0 0 0 0]
[0 0 0 0]
Bases: sage.modules.matrix_morphism.MatrixMorphism_abstract
A morphism between modular abelian varieties. EXAMPLES:
sage: t = J0(11).hecke_operator(2)
sage: from sage.modular.abvar.morphism import Morphism
sage: isinstance(t, Morphism)
True
Return the cokernel of self.
OUTPUT:
EXAMPLES:
sage: t = J0(33).hecke_operator(2)
sage: (t-1).cokernel()
(Abelian subvariety of dimension 1 of J0(33),
Abelian variety morphism:
From: Abelian variety J0(33) of dimension 3
To: Abelian subvariety of dimension 1 of J0(33))
Projection will always have cokernel zero.
sage: J0(37).projection(J0(37)[0]).cokernel()
(Simple abelian subvariety of dimension 0 of J0(37),
Abelian variety morphism:
From: Simple abelian subvariety 37a(1,37) of dimension 1 of J0(37)
To: Simple abelian subvariety of dimension 0 of J0(37))
Here we have a nontrivial cokernel of a Hecke operator, as the T_2-eigenvalue for the newform 37b is 0.
sage: J0(37).hecke_operator(2).cokernel()
(Abelian subvariety of dimension 1 of J0(37),
Abelian variety morphism:
From: Abelian variety J0(37) of dimension 2
To: Abelian subvariety of dimension 1 of J0(37))
sage: AbelianVariety('37b').newform().q_expansion(5)
q + q^3 - 2*q^4 + O(q^5)
Returns the complementary isogeny of self.
EXAMPLES:
sage: J = J0(43)
sage: A = J[1]
sage: T5 = A.hecke_operator(5)
sage: T5.is_isogeny()
True
sage: T5.complementary_isogeny()
Abelian variety endomorphism of Simple abelian subvariety 43b(1,43) of dimension 2 of J0(43)
sage: (T5.complementary_isogeny() * T5).matrix()
[2 0 0 0]
[0 2 0 0]
[0 0 2 0]
[0 0 0 2]
View self as a morphism 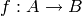 . Then
. Then 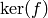 is an extension of an abelian variety
is an extension of an abelian variety  by a finite
component group
by a finite
component group  . This function constructs a morphism
. This function constructs a morphism
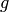 with domain
with domain  and codomain Q isogenous to
and codomain Q isogenous to
 such that
such that 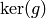 is equal to
is equal to  .
.
OUTPUT: a morphism
EXAMPLES:
sage: A,B,C = J0(33)
sage: pi = J0(33).projection(A)
sage: pi.kernel()
(Finite subgroup with invariants [5] over QQbar of Abelian variety J0(33) of dimension 3,
Abelian subvariety of dimension 2 of J0(33))
sage: psi = pi.factor_out_component_group()
sage: psi.kernel()
(Finite subgroup with invariants [] over QQbar of Abelian variety J0(33) of dimension 3,
Abelian subvariety of dimension 2 of J0(33))
ALGORITHM: We compute a subgroup  of
of  so that
the composition
so that
the composition 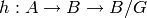 has kernel that
contains
has kernel that
contains ![A[n]](../../../_images/math/709d19d892be8f16edd309911617557ce0ae32a5.png) and component group isomorphic to
and component group isomorphic to
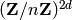 , where
, where  is the
dimension of
is the
dimension of  . Then
. Then 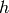 factors through
multiplication by
factors through
multiplication by  , so there is a morphism
, so there is a morphism
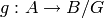 such that
such that ![g \circ [n] = h](../../../_images/math/1f0cf3bb579b2d9e468709523c549e99f8cd9e6b.png) . Then
. Then
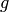 is the desired morphism. We give more details below
about how to transform this into linear algebra.
is the desired morphism. We give more details below
about how to transform this into linear algebra.
Return the image of this morphism.
OUTPUT: an abelian variety
EXAMPLES: We compute the image of projection onto a factor of
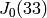 :
:
sage: A,B,C = J0(33)
sage: A
Simple abelian subvariety 11a(1,33) of dimension 1 of J0(33)
sage: f = J0(33).projection(A)
sage: f.image()
Abelian subvariety of dimension 1 of J0(33)
sage: f.image() == A
True
We compute the image of a Hecke operator:
sage: t2 = J0(33).hecke_operator(2); t2.fcp()
(x - 1) * (x + 2)^2
sage: phi = t2 + 2
sage: phi.image()
Abelian subvariety of dimension 1 of J0(33)
The sum of the image and the kernel is the whole space:
sage: phi.kernel()[1] + phi.image() == J0(33)
True
Return True if this morphism is an isogeny of abelian varieties.
EXAMPLES:
sage: J = J0(39)
sage: Id = J.hecke_operator(1)
sage: Id.is_isogeny()
True
sage: J.hecke_operator(19).is_isogeny()
False
Return the kernel of this morphism.
OUTPUT:
EXAMPLES: We compute the kernel of a projection map. Notice that the kernel has a nontrivial abelian variety part.
sage: A, B, C = J0(33)
sage: pi = J0(33).projection(B)
sage: pi.kernel()
(Finite subgroup with invariants [20] over QQbar of Abelian variety J0(33) of dimension 3,
Abelian subvariety of dimension 2 of J0(33))
We compute the kernels of some Hecke operators:
sage: t2 = J0(33).hecke_operator(2)
sage: t2
Hecke operator T_2 on Abelian variety J0(33) of dimension 3
sage: t2.kernel()
(Finite subgroup with invariants [2, 2, 2, 2] over QQ of Abelian variety J0(33) of dimension 3,
Abelian subvariety of dimension 0 of J0(33))
sage: t3 = J0(33).hecke_operator(3)
sage: t3.kernel()
(Finite subgroup with invariants [3, 3] over QQ of Abelian variety J0(33) of dimension 3,
Abelian subvariety of dimension 0 of J0(33))