-series of modular abelian varieties

At the moment very little functionality is implemented – this is mostly a placeholder for future planned work.

AUTHOR:

• William Stein (2007-03)

TESTS:

sage: L = J0(37)[0].padic_lseries(5)
sage: loads(dumps(L)) == L
True
sage: L = J0(37)[0].lseries()
sage: loads(dumps(L)) == L
True

class sage.modular.abvar.lseries.Lseries(abvar)

Bases: sage.structure.sage_object.SageObject

Base class for -series attached to modular abelian varieties.

abelian_variety()

Return the abelian variety that this -series is attached to.

OUTPUT:

a modular abelian variety

EXAMPLES:

sage: J0(11).padic_lseries(7).abelian_variety()
Abelian variety J0(11) of dimension 1

class sage.modular.abvar.lseries.Lseries_complex(abvar)

Bases: sage.modular.abvar.lseries.Lseries

A complex -series attached to a modular abelian variety.

EXAMPLES:

sage: A = J0(37)
sage: A.lseries()
Complex L-series attached to Abelian variety J0(37) of dimension 2

rational_part()

Return the rational part of this -function at the central critical value 1.

NOTE: This is not yet implemented.

EXAMPLES:

sage: J0(37).lseries().rational_part()
...
NotImplementedError

class sage.modular.abvar.lseries.Lseries_padic(abvar, p)

Bases: sage.modular.abvar.lseries.Lseries

A -adic -series attached to a modular abelian variety.

power_series(n=2, prec=5)

Return the -th approximation to this -adic -series as a power series in 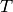. Each coefficient is a -adic number whose precision is provably correct.

NOTE: This is not yet implemented.

EXAMPLES:

sage: L = J0(37)[0].padic_lseries(5)
sage: L.power_series()
...
NotImplementedError
sage: L.power_series(3,7)
...
NotImplementedError

prime()

Return the prime of this -adic -series.

EXAMPLES:

sage: J0(11).padic_lseries(7).prime()
7