Miscellaneous functions¶

AUTHORS:

William Stein
William Stein (2006-04-26): added workaround for Windows where most users’ home directory has a space in it.
Robert Bradshaw (2007-09-20): Ellipsis range/iterator.

TESTS:

Check the fix from trac #8323:

sage: globals().has_key('name')
False
sage: globals().has_key('func')
False

class sage.misc.misc.AttrCallObject(name, args, kwds)¶: Bases: object

class sage.misc.misc.DeprecatedFunctionAlias(func, version)¶

Bases: object

A wrapper around methods or functions which automatically print the correct deprecation message. See deprecated_function_alias().

AUTHORS:

Florent Hivert (2009-11-23), with the help of Mike Hansen.

class sage.misc.misc.GlobalCputime(t)¶

Container for CPU times of subprocesses.

AUTHOR:

Martin Albrecht - (2008-12): initial version

EXAMPLE:

Objects of this type are returned if subprocesses=True is passed to cputime():

sage: cputime(subprocesses=True) # indirect doctest, output random
0.2347431

We can use it to keep track of the CPU time spent in Singular for example:

sage: t = cputime(subprocesses=True)
sage: P = PolynomialRing(QQ,7,'x')
sage: I = sage.rings.ideal.Katsura(P)
sage: gb = I.groebner_basis() # calls Singular
sage: cputime(subprocesses=True) - t # output random
0.462987

For further processing we can then convert this container to a float:

sage: t = cputime(subprocesses=True)
sage: float(t) #output somewhat random
2.1088339999999999

See also ellipsis_range.

Use (1,2,...) notation.

EXAMPLES:

sage: A = ellipsis_iter(1,2,Ellipsis)
sage: [A.next() for _ in range(10)]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sage: A.next()
11
sage: A = ellipsis_iter(1,3,5,Ellipsis)
sage: [A.next() for _ in range(10)]
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
sage: A = ellipsis_iter(1,2,Ellipsis,5,10,Ellipsis)
sage: [A.next() for _ in range(10)]
[1, 2, 3, 4, 5, 10, 11, 12, 13, 14]

TESTS:

These were carefully chosen tests, only to be changed if the semantics of ellipsis ranges change. In other words, if they don’t pass it’s probably a bug in the implementation, not in the doctest.

sage: list(1,..,10)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sage: list(1,3,..,10)
[1, 3, 5, 7, 9]
sage: list(1,..,10,..,20)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
sage: list(1,3,..,10,..,20)
[1, 3, 5, 7, 9, 10, 12, 14, 16, 18, 20]
sage: list(1,3,..,10,10,..,20)
[1, 3, 5, 7, 9, 10, 12, 14, 16, 18, 20]
sage: list(0,2,..,10,10,..,20,20,..,25)
[0, 2, 4, 6, 8, 10, 10, 12, 14, 16, 18, 20, 20, 22, 24]
sage: list(10,..,1)
[]
sage: list(10,11,..,1)
[]
sage: list(10,9,..,1)
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
sage: list(100,..,10,..,20)
[10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
sage: list(0,..,10,..,-20)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sage: list(100,..,10,..,-20)
[]
sage: list(100,102,..,10,..,20)
[10, 12, 14, 16, 18, 20]

sage.misc.misc.ellipsis_range(*args, **kwds)¶

Return arithmetic sequence determined by the numeric arguments and ellipsis. Best illustrated by examples.

Use [1,2,..,n] notation.

EXAMPLES:

sage: ellipsis_range(1,Ellipsis,11,100)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 100]
sage: ellipsis_range(0,2,Ellipsis,10,Ellipsis,20)
[0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
sage: ellipsis_range(0,2,Ellipsis,11,Ellipsis,20)
[0, 2, 4, 6, 8, 10, 11, 13, 15, 17, 19]
sage: ellipsis_range(0,2,Ellipsis,11,Ellipsis,20, step=3)
[0, 2, 5, 8, 11, 14, 17, 20]
sage: ellipsis_range(10,Ellipsis,0)
[]

TESTS: These were carefully chosen tests, only to be changed if the semantics of ellipsis ranges change. In other words, if they don’t pass it’s probably a bug in the implementation, not in the doctest.

Note 10 only appears once (though it is in both ranges).

sage: ellipsis_range(0,Ellipsis,10,Ellipsis,20,step=2)
[0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20]

Sometimes one or more ranges is empty.

sage: ellipsis_range(100,Ellipsis,10,Ellipsis,20,step=2)
[10, 12, 14, 16, 18, 20]
sage: ellipsis_range(0,Ellipsis,10,Ellipsis,-20,step=2)
[0, 2, 4, 6, 8, 10]
sage: ellipsis_range(100,Ellipsis,10,Ellipsis,-20,step=2)
[]

We always start on the leftmost point of the range.

sage: ellipsis_range(0,Ellipsis,10,Ellipsis,20,step=3)
[0, 3, 6, 9, 10, 13, 16, 19]
sage: ellipsis_range(100,Ellipsis,10,Ellipsis,20,step=3)
[10, 13, 16, 19]
sage: ellipsis_range(0,Ellipsis,10,Ellipsis,-20,step=3)
[0, 3, 6, 9]
sage: ellipsis_range(100,Ellipsis,10,Ellipsis,-20,step=3)
[]
sage: ellipsis_range(0,1,Ellipsis,-10)
[]
sage: ellipsis_range(0,1,Ellipsis,-10,step=1)
[0]
sage: ellipsis_range(100,0,1,Ellipsis,-10)
[100]

Note the duplicate 5 in the output.

sage: ellipsis_range(0,Ellipsis,5,5,Ellipsis,10)
[0, 1, 2, 3, 4, 5, 5, 6, 7, 8, 9, 10]

Examples in which the step determines the parent of the elements:

sage: [1..3, step=0.5]
[1.00000000000000, 1.50000000000000, 2.00000000000000, 2.50000000000000, 3.00000000000000]
sage: v = [1..5, step=1/1]; v
[1, 2, 3, 4, 5]
sage: parent(v[2])
Rational Field

sage.misc.misc.embedded()¶

Return True if this copy of Sage is running embedded in the Sage notebook.

EXAMPLES:

sage: sage.misc.misc.embedded()    # output True if in the notebook
False

sage.misc.misc.exists(S, P)¶

If S contains an element x such that P(x) is True, this function returns True and the element x. Otherwise it returns False and None.

Note that this function is NOT suitable to be used in an if-statement or in any place where a boolean expression is expected. For those situations, use the Python built-in

any(P(x) for x in S)

INPUT:

S - object (that supports enumeration)
P - function that returns True or False

OUTPUT:

bool - whether or not P is True for some element x of S
object - x

EXAMPLES: lambda functions are very useful when using the exists function:

sage: exists([1,2,5], lambda x : x > 7)
(False, None)
sage: exists([1,2,5], lambda x : x > 3)
(True, 5)

The following example is similar to one in the MAGMA handbook. We check whether certain integers are a sum of two (small) cubes:

sage: cubes = [t**3 for t in range(-10,11)]
sage: exists([(x,y) for x in cubes for y in cubes], lambda v : v[0]+v[1] == 218)
(True, (-125, 343))
sage: exists([(x,y) for x in cubes for y in cubes], lambda v : v[0]+v[1] == 219)
(False, None)

sage.misc.misc.forall(S, P)¶

If P(x) is true every x in S, return True and None. If there is some element x in S such that P is not True, return False and x.

Note that this function is NOT suitable to be used in an if-statement or in any place where a boolean expression is expected. For those situations, use the Python built-in

all(P(x) for x in S)

INPUT:

S - object (that supports enumeration)
P - function that returns True or False

OUTPUT:

bool - whether or not P is True for all elements of S
object - x

EXAMPLES: lambda functions are very useful when using the forall function. As a toy example we test whether certain integers are greater than 3.

sage: forall([1,2,5], lambda x : x > 3)
(False, 1)
sage: forall([1,2,5], lambda x : x > 0)
(True, None)

Next we ask whether every positive integer less than 100 is a product of at most 2 prime factors:

sage: forall(range(1,100),  lambda n : len(factor(n)) <= 2)
(False, 30)

The answer is no, and 30 is a counterexample. However, every positive integer 100 is a product of at most 3 primes.

sage: forall(range(1,100),  lambda n : len(factor(n)) <= 3)
(True, None)

sage.misc.misc.generic_cmp(x, y)¶

Compare x and y and return -1, 0, or 1.

This is similar to x.__cmp__(y), but works even in some cases when a .__cmp__ method isn’t defined.

sage.misc.misc.get_verbose()¶

Return the global Sage verbosity level.

INPUT: int level: an integer between 0 and 2, inclusive.

OUTPUT: changes the state of the verbosity flag.

EXAMPLES:

sage: get_verbose()
0
sage: set_verbose(2)
sage: get_verbose()
2
sage: set_verbose(0)

sage.misc.misc.get_verbose_files()¶

sage.misc.misc.getitem(v, n)¶

Variant of getitem that coerces to an int if a TypeError is raised.

(This is not needed anymore - classes should define an __index__ method.)

Thus, e.g., getitem(v,n) will work even if $v$ is a Python list and $n$ is a Sage integer.

EXAMPLES:

sage: v = [1,2,3]

The following used to fail in Sage <= 1.3.7. Now it works fine:

sage: v[ZZ(1)]          
2

This always worked.

sage: getitem(v, ZZ(1))
2

sage.misc.misc.graphics_filename(ext='png')¶: Return the next available canonical filename for a plot/graphics file.

class sage.misc.misc.infix_operator(precedence)¶

Bases: object

A decorator for functions which allows for a hack that makes the function behave like an infix operator.

This decorator exists as a convenience for interactive use.

EXAMPLES:

An infix dot product operator:

sage: def dot(a,b): return a.dot_product(b)
sage: dot=infix_operator('multiply')(dot)
sage: u=vector([1,2,3])
sage: v=vector([5,4,3])
sage: u *dot* v
22

An infix element-wise addition operator:

sage: def eadd(a,b): 
...     return a.parent([i+j for i,j in zip(a,b)])
sage: eadd=infix_operator('add')(eadd)
sage: u=vector([1,2,3])
sage: v=vector([5,4,3])
sage: u +eadd+ v
(6, 6, 6)
sage: 2*u +eadd+ v
(7, 8, 9)

A hack to simulate a postfix operator:

sage: def thendo(a,b): return b(a)
sage: thendo=infix_operator('or')(thendo)
sage: x |thendo| cos |thendo| (lambda x: x^2)
cos(x)^2

sage.misc.misc.inject_variable(name, value)¶

inject a variable into the main global namespace

INPUT:

name - a string
value - anything

EXAMPLES:

sage: from sage.misc.misc import inject_variable
sage: inject_variable("a", 314)
sage: a
314

A warning is issued the first time an existing value is overwritten:

sage: inject_variable("a", 271)
doctest:...: RuntimeWarning: redefining global value `a`
sage: a
271
sage: inject_variable("a", 272)
sage: a
272

That’s because warn seem to not reissue twice the same warning:

sage: from warnings import warn sage: warn(“blah”) doctest:1: UserWarning: blah sage: warn(“blah”)

Use with care!

sage.misc.misc.inject_variable_test(name, value, depth)¶

A function for testing deep calls to inject_variable

TESTS:

sage: from sage.misc.misc import inject_variable_test
sage: inject_variable_test("a0", 314, 0)
sage: a0
314
sage: inject_variable_test("a1", 314, 1)
sage: a1
314
sage: inject_variable_test("a2", 314, 2)
sage: a2
314
sage: inject_variable_test("a2", 271, 2)
doctest:...: RuntimeWarning: redefining global value `a2`
sage: a2
271

sage.misc.misc.is_in_string(line, pos)¶

Returns True if the character at position pos in line occurs within a string.

EXAMPLES:

sage: from sage.misc.misc import is_in_string
sage: line = 'test(\'#\')'
sage: is_in_string(line, line.rfind('#'))
True
sage: is_in_string(line, line.rfind(')'))
False

sage.misc.misc.is_iterator(it)¶

Tests if it is an iterator.

The mantra if hasattr(it, 'next') was used to tests if it is an iterator. This is not quite correct since it could have a next methods with a different semantic.

EXAMPLES:

sage: it = iter([1,2,3])
sage: is_iterator(it)
True

sage: class wrong():
...      def __init__(self): self.n = 5
...      def next(self):
...          self.n -= 1
...          if self.n == 0: raise StopIteration
...          return self.n
sage: x = wrong()
sage: is_iterator(x)
False
sage: list(x)
...
TypeError: iteration over non-sequence

sage: class good(wrong):
...      def __iter__(self): return self
sage: x = good()
sage: is_iterator(x)
True
sage: list(x)
[4, 3, 2, 1]

sage: P = Partitions(3)
sage: is_iterator(P)
False
sage: is_iterator(iter(P))
True

class sage.misc.misc.lazy_prop(calculate_function)¶: Bases: object

sage.misc.misc.newton_method_sizes(N)¶

Returns a sequence of integers 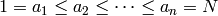$1 = a_1 \leq a_2 \leq \cdots \leq a_n = N$ such that 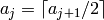$a_j = \lceil a_{j+1} / 2 \rceil$ for all $j$ .

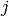This is useful for Newton-style algorithms that double the precision at each stage. For example if you start at precision 1 and want an answer to precision 17, then it’s better to use the intermediate stages 1, 2, 3, 5, 9, 17 than to use 1, 2, 4, 8, 16, 17.

INPUT:

N - positive integer

EXAMPLES:

sage: newton_method_sizes(17)
[1, 2, 3, 5, 9, 17]
sage: newton_method_sizes(16)
[1, 2, 4, 8, 16]
sage: newton_method_sizes(1)
[1]

AUTHORS:

David Harvey (2006-09-09)

sage.misc.misc.pad_zeros(s, size=3)¶

EXAMPLES:

sage: pad_zeros(100)
'100'
sage: pad_zeros(10)
'010'
sage: pad_zeros(10, 5)
'00010'
sage: pad_zeros(389, 5)
'00389'
sage: pad_zeros(389, 10)
'0000000389'

sage.misc.misc.powerset(X)¶

Iterator over the list of all subsets of the iterable X, in no particular order. Each list appears exactly once, up to order.

INPUT:

X - an iterable

OUTPUT: iterator of lists

EXAMPLES:

sage: list(powerset([1,2,3]))
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
sage: [z for z in powerset([0,[1,2]])]
[[], [0], [[1, 2]], [0, [1, 2]]]

Iterating over the power set of an infinite set is also allowed:

sage: i = 0
sage: for x in powerset(ZZ):
...    if i > 10:
...       break
...    else:
...       i += 1
...    print x,
[] [0] [1] [0, 1] [-1] [0, -1] [1, -1] [0, 1, -1] [2] [0, 2] [1, 2]

You may also use subsets as an alias for powerset:

sage: subsets([1,2,3])   # random object location in output
<generator object at 0xaeae418c>
sage: list(subsets([1,2,3]))
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

The reason we return lists instead of sets is that the elements of
sets must be hashable and many structures on which one wants the
powerset consist of non-hashable objects.

AUTHORS:

William Stein
Nils Bruin (2006-12-19): rewrite to work for not-necessarily finite objects X.

sage.misc.misc.prop(f)¶

sage.misc.misc.random_sublist(X, s)¶

Return a pseudo-random sublist of the list X where the probability of including a particular element is s.

INPUT:

X - list
s - floating point number between 0 and 1

OUTPUT: list

EXAMPLES:

sage: S = [1,7,3,4,18]
sage: random_sublist(S, 0.5)
[1, 3, 4]
sage: random_sublist(S, 0.5)
[1, 3]

sage.misc.misc.repr_lincomb(symbols, coeffs, is_latex=False)¶

Compute a string representation of a linear combination of some formal symbols.

INPUT:

symbols - list of symbols
coeffs - list of coefficients of the symbols

OUTPUT:

str - a string

EXAMPLES:

sage: repr_lincomb(['a','b','c'], [1,2,3])
'a + 2*b + 3*c'
sage: repr_lincomb(['a','b','c'], [1,'2+3*x',3])
'a + (2+3*x)*b + 3*c'
sage: repr_lincomb(['a','b','c'], ['1+x^2','2+3*x',3])
'(1+x^2)*a + (2+3*x)*b + 3*c'
sage: repr_lincomb(['a','b','c'], ['1+x^2','-2+3*x',3])
'(1+x^2)*a + (-2+3*x)*b + 3*c'
sage: repr_lincomb(['a','b','c'], [1,-2,-3])
'a - 2*b - 3*c'
sage: t = PolynomialRing(RationalField(),'t').gen()
sage: repr_lincomb(['a', 's', ''], [-t,t-2,t**2+2])
'-t*a + (t-2)*s + (t^2+2)'

sage.misc.misc.sage_wraps(wrapped, assigned=('__module__', '__name__', '__doc__'), updated=('__dict__', ))¶

Decorator factory to apply update_wrapper() to a wrapper function, and additionally add a _sage_src_ attribute for Sage introspection.

Use this exactly like @wraps from the functools module.

EXAMPLES:

sage: from sage.misc.misc import sage_wraps
sage: def square(f):
...     @sage_wraps(f)
...     def new_f(x):
...         return f(x)*f(x)
...     return new_f
sage: @square
... def g(x):
...     "My little function"
...     return x
sage: g(2)
4
sage: g(x)
x^2
sage: g._sage_src_()
'@square...def g(x)...'
sage: g.__doc__
'My little function'

sage.misc.misc.set_verbose(level, files='all')¶

Set the global Sage verbosity level.

INPUT:

level - an integer between 0 and 2, inclusive.
files (default: ‘all’): list of files to make verbose, or

‘all’ to make ALL files verbose (the default).

OUTPUT: changes the state of the verbosity flag and possibly appends to the list of files that are verbose.

EXAMPLES:

sage: set_verbose(2)
sage: verbose("This is Sage.", level=1)  # not tested
VERBOSE1 (?): This is Sage.
sage: verbose("This is Sage.", level=2)  # not tested
VERBOSE2 (?): This is Sage.
sage: verbose("This is Sage.", level=3)  # not tested
[no output]
sage: set_verbose(0)

sage.misc.misc.set_verbose_files(file_name)¶

sage.misc.misc.sourcefile(object)¶: Work out which source or compiled file an object was defined in.

sage.misc.misc.srange(start, end=None, step=1, universe=None, check=True, include_endpoint=False, endpoint_tolerance=1.0000000000000001e-05)¶

Return list of numbers a, a+step, ..., a+k*step, where a+k*step < b and a+(k+1)*step >= b over exact rings, and makes a best attempt for inexact rings (see note below).

This provides one way to iterate over Sage integers as opposed to Python int’s. It also allows you to specify step sizes for such an iteration. Note, however, that what is returned is a full list of Integers and not an iterator. It is potentially much slower than the Python range function, depending on the application. The function xsrange() provides an iterator with similar functionality which would usually be more efficient than using srange().

INPUT:

a - number
b - number (default: None)
step - number (default: 1)
universe - Parent or type where all the elements should live (default: deduce from inputs)
check - make sure a, b, and step all lie in the same universe
include_endpoint - whether or not to include the endpoint (default: False)
endpoint_tolerance - used to determine whether or not the endpoint is hit for inexact rings (default 1e-5)

OUTPUT:

list

If b is None, then b is set equal to a and a is set equal to the 0 in the parent of b.

Unlike range, a and b can be any type of numbers, and the resulting list involves numbers of that type.

Note

The list elements are computed via repeated addition rather than multiplication, which may produce slightly different results with inexact rings. For example:

sage: sum([1.1] * 10) == 1.1 * 10
False

Also, the question of whether the endpoint is hit exactly for a given a + k*step is fuzzy for an inexact ring. If a + k*step = b for some k within endpoint_tolerance of being integral, it is considered an exact hit, thus avoiding spurious values falling just below the endpoint.

Note

This function is called srange to distinguish it from the built-in Python range command. The s at the beginning of the name stands for “Sage”.

EXAMPLES:

sage: v = srange(5); v
[0, 1, 2, 3, 4]
sage: type(v[2])
<type 'sage.rings.integer.Integer'>
sage: srange(1, 10)
[1, 2, 3, 4, 5, 6, 7, 8, 9]
sage: srange(10, 1, -1)
[10, 9, 8, 7, 6, 5, 4, 3, 2]
sage: srange(10,1,-1, include_endpoint=True)
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
sage: srange(1, 10, universe=RDF)
[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0]

sage: srange(1, 10, 1/2)
[1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2, 5, 11/2, 6, 13/2, 7, 15/2, 8, 17/2, 9, 19/2]    
sage: srange(1, 5, 0.5)
[1.00000000000000, 1.50000000000000, 2.00000000000000, 2.50000000000000, 3.00000000000000, 3.50000000000000, 4.00000000000000, 4.50000000000000]
sage: srange(0, 1, 0.4)
[0.000000000000000, 0.400000000000000, 0.800000000000000]
sage: srange(1.0, 5.0, include_endpoint=True)
[1.00000000000000, 2.00000000000000, 3.00000000000000, 4.00000000000000, 5.00000000000000]
sage: srange(1.0, 1.1)
[1.00000000000000]
sage: srange(1.0, 1.0)
[]
sage: V = VectorSpace(QQ, 2)
sage: srange(V([0,0]), V([5,5]), step=V([2,2]))
[(0, 0), (2, 2), (4, 4)]

Including the endpoint:

sage: srange(0, 10, step=2, include_endpoint=True)
[0, 2, 4, 6, 8, 10]
sage: srange(0, 10, step=3, include_endpoint=True)
[0, 3, 6, 9]

Try some inexact rings:

sage: srange(0.5, 1.1, 0.1, universe=RDF, include_endpoint=False)
[0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
sage: srange(0.5, 1, 0.1, universe=RDF, include_endpoint=False)
[0.5, 0.6, 0.7, 0.8, 0.9]
sage: srange(0.5, 0.9, 0.1, universe=RDF, include_endpoint=False)
[0.5, 0.6, 0.7, 0.8]
sage: srange(0, 1.1, 0.1, universe=RDF, include_endpoint=True)
[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1]
sage: srange(0, 0.2, 0.1, universe=RDF, include_endpoint=True)
[0.0, 0.1, 0.2]
sage: srange(0, 0.3, 0.1, universe=RDF, include_endpoint=True)
[0.0, 0.1, 0.2, 0.3]

sage.misc.misc.strunc(s, n=60)¶: Truncate at first space after position n, adding ‘...’ if nontrivial truncation.

sage.misc.misc.subsets(X)¶

Iterator over the list of all subsets of the iterable X, in no particular order. Each list appears exactly once, up to order.

INPUT:

X - an iterable

OUTPUT: iterator of lists

EXAMPLES:

sage: list(powerset([1,2,3]))
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
sage: [z for z in powerset([0,[1,2]])]
[[], [0], [[1, 2]], [0, [1, 2]]]

Iterating over the power set of an infinite set is also allowed:

sage: i = 0
sage: for x in powerset(ZZ):
...    if i > 10:
...       break
...    else:
...       i += 1
...    print x,
[] [0] [1] [0, 1] [-1] [0, -1] [1, -1] [0, 1, -1] [2] [0, 2] [1, 2]

You may also use subsets as an alias for powerset:

sage: subsets([1,2,3])   # random object location in output
<generator object at 0xaeae418c>
sage: list(subsets([1,2,3]))
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

The reason we return lists instead of sets is that the elements of
sets must be hashable and many structures on which one wants the
powerset consist of non-hashable objects.

AUTHORS:

William Stein
Nils Bruin (2006-12-19): rewrite to work for not-necessarily finite objects X.

sage.misc.misc.sxrange(start, end=None, step=1, universe=None, check=True, include_endpoint=False, endpoint_tolerance=1.0000000000000001e-05)¶

Return an iterator over numbers a, a+step, ..., a+k*step, where a+k*step < b and a+(k+1)*step > b.

INPUT:: universe – Parent or type where all the elements should live (default: deduce from inputs) check – make sure a, b, and step all lie in the same universe include_endpoint – whether or not to include the endpoint (default: False) endpoint_tolerance – used to determine whether or not the endpoint is hit for inexact rings (default 1e-5)

a - number
b - number
step - number (default: 1)

OUTPUT: iterator

Unlike range, a and b can be any type of numbers, and the resulting iterator involves numbers of that type.

Miscellaneous functions¶

Previous topic

Next topic

This Page

Navigation

Miscellaneous functions¶

Previous topic

Next topic

This Page

Quick search

Navigation