Matrix Constructor.¶

sage.matrix.constructor.Matrix(*args, **kwds)¶

Create a matrix.

INPUT: The matrix command takes the entries of a matrix, optionally preceded by a ring and the dimensions of the matrix, and returns a matrix.

The entries of a matrix can be specified as a flat list of elements, a list of lists (i.e., a list of rows), a list of Sage vectors, a callable object, or a dictionary having positions as keys and matrix entries as values (see the examples). If you pass in a callable object, then you must specify the number of rows and columns. You can create a matrix of zeros by passing an empty list or the integer zero for the entries. To construct a multiple of the identity (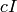 $cI$ ), you can specify square dimensions and pass in $c$ . Calling matrix() with a Sage object may return something that makes sense. Calling matrix() with a NumPy array will convert the array to a matrix.

The ring, number of rows, and number of columns of the matrix can be specified by setting the ring, nrows, or ncols parameters or by passing them as the first arguments to the function in the order ring, nrows, ncols. The ring defaults to ZZ if it is not specified or cannot be determined from the entries. If the numbers of rows and columns are not specified and cannot be determined, then an empty 0x0 matrix is returned.

ring - the base ring for the entries of the matrix.
nrows - the number of rows in the matrix.
ncols - the number of columns in the matrix.
sparse - create a sparse matrix. This defaults to True when the entries are given as a dictionary, otherwise defaults to False.

OUTPUT:

a matrix

EXAMPLES:

sage: m=matrix(2); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring

sage: m=matrix(2,3); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring

sage: m=matrix(QQ,[[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field

sage: m = matrix(QQ, 3, 3, lambda i, j: i+j); m
[0 1 2]
[1 2 3]
[2 3 4]
sage: m = matrix(3, lambda i,j: i-j); m
[ 0 -1 -2]
[ 1  0 -1]
[ 2  1  0]

sage: v1=vector((1,2,3))
sage: v2=vector((4,5,6))
sage: m=matrix([v1,v2]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring

sage: m=matrix(QQ,2,[1,2,3,4,5,6]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field

sage: m=matrix(QQ,2,3,[1,2,3,4,5,6]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field

sage: m=matrix({(0,1): 2, (1,1):2/5}); m; m.parent()
[  0   2]
[  0 2/5]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field

sage: m=matrix(QQ,2,3,{(1,1): 2}); m; m.parent()
[0 0 0]
[0 2 0]
Full MatrixSpace of 2 by 3 sparse matrices over Rational Field

sage: import numpy
sage: n=numpy.array([[1,2],[3,4]],float)
sage: m=matrix(n); m; m.parent()
[1.0 2.0]
[3.0 4.0]
Full MatrixSpace of 2 by 2 dense matrices over Real Double Field

sage: v = vector(ZZ, [1, 10, 100])
sage: m=matrix(v); m; m.parent()
[  1  10 100]
Full MatrixSpace of 1 by 3 dense matrices over Integer Ring
sage: m=matrix(GF(7), v); m; m.parent()
[1 3 2]
Full MatrixSpace of 1 by 3 dense matrices over Finite Field of size 7

sage: g = graphs.PetersenGraph()
sage: m = matrix(g); m; m.parent()
[0 1 0 0 1 1 0 0 0 0]
[1 0 1 0 0 0 1 0 0 0]
[0 1 0 1 0 0 0 1 0 0]
[0 0 1 0 1 0 0 0 1 0]
[1 0 0 1 0 0 0 0 0 1]
[1 0 0 0 0 0 0 1 1 0]
[0 1 0 0 0 0 0 0 1 1]
[0 0 1 0 0 1 0 0 0 1]
[0 0 0 1 0 1 1 0 0 0]
[0 0 0 0 1 0 1 1 0 0]
Full MatrixSpace of 10 by 10 dense matrices over Integer Ring

sage: matrix(ZZ, 10, 10, range(100), sparse=True).parent()
Full MatrixSpace of 10 by 10 sparse matrices over Integer Ring

sage: R = PolynomialRing(QQ, 9, 'x')
sage: A = matrix(R, 3, 3, R.gens()); A
[x0 x1 x2]
[x3 x4 x5]
[x6 x7 x8]
sage: det(A)
-x2*x4*x6 + x1*x5*x6 + x2*x3*x7 - x0*x5*x7 - x1*x3*x8 + x0*x4*x8

TESTS:

sage: m=matrix(); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(QQ); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Rational Field
sage: m=matrix(QQ,2); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: m=matrix(QQ,2,3); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix([]); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(QQ,[]); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Rational Field
sage: m=matrix(2,2,1); m; m.parent()
[1 0]
[0 1]
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: m=matrix(QQ,2,2,1); m; m.parent()
[1 0]
[0 1]
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: m=matrix(2,3,0); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring
sage: m=matrix(QQ,2,3,0); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix([[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring
sage: m=matrix(QQ,2,[[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix(QQ,3,[[1,2,3],[4,5,6]]); m; m.parent()
...
ValueError: Number of rows does not match up with specified number.
sage: m=matrix(QQ,2,3,[[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix(QQ,2,4,[[1,2,3],[4,5,6]]); m; m.parent()
...
ValueError: Number of columns does not match up with specified number.
sage: m=matrix([(1,2,3),(4,5,6)]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring
sage: m=matrix([1,2,3,4,5,6]); m; m.parent()
[1 2 3 4 5 6]
Full MatrixSpace of 1 by 6 dense matrices over Integer Ring
sage: m=matrix((1,2,3,4,5,6)); m; m.parent()
[1 2 3 4 5 6]
Full MatrixSpace of 1 by 6 dense matrices over Integer Ring
sage: m=matrix(QQ,[1,2,3,4,5,6]); m; m.parent()
[1 2 3 4 5 6]
Full MatrixSpace of 1 by 6 dense matrices over Rational Field
sage: m=matrix(QQ,3,2,[1,2,3,4,5,6]); m; m.parent()
[1 2]
[3 4]
[5 6]
Full MatrixSpace of 3 by 2 dense matrices over Rational Field
sage: m=matrix(QQ,2,4,[1,2,3,4,5,6]); m; m.parent()
...
ValueError: entries has the wrong length
sage: m=matrix(QQ,5,[1,2,3,4,5,6]); m; m.parent()
...
TypeError: entries has the wrong length
sage: m=matrix({(1,1): 2}); m; m.parent()
[0 0]
[0 2]
Full MatrixSpace of 2 by 2 sparse matrices over Integer Ring
sage: m=matrix(QQ,{(1,1): 2}); m; m.parent()
[0 0]
[0 2]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: m=matrix(QQ,3,{(1,1): 2}); m; m.parent()
[0 0 0]
[0 2 0]
[0 0 0]
Full MatrixSpace of 3 by 3 sparse matrices over Rational Field
sage: m=matrix(QQ,3,4,{(1,1): 2}); m; m.parent()
[0 0 0 0]
[0 2 0 0]
[0 0 0 0]
Full MatrixSpace of 3 by 4 sparse matrices over Rational Field
sage: m=matrix(QQ,2,{(1,1): 2}); m; m.parent()
[0 0]
[0 2]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: m=matrix(QQ,1,{(1,1): 2}); m; m.parent()
...
IndexError: invalid entries list
sage: m=matrix({}); m; m.parent()
[]
Full MatrixSpace of 0 by 0 sparse matrices over Integer Ring
sage: m=matrix(QQ,{}); m; m.parent()
[]
Full MatrixSpace of 0 by 0 sparse matrices over Rational Field
sage: m=matrix(QQ,2,{}); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: m=matrix(QQ,2,3,{}); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 sparse matrices over Rational Field
sage: m=matrix(2,{}); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 sparse matrices over Integer Ring
sage: m=matrix(2,3,{}); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 sparse matrices over Integer Ring
sage: m=matrix(0); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(0,2); m; m.parent()
[]
Full MatrixSpace of 0 by 2 dense matrices over Integer Ring
sage: m=matrix(2,0); m; m.parent()
[]
Full MatrixSpace of 2 by 0 dense matrices over Integer Ring
sage: m=matrix(0,[1]); m; m.parent()
...
ValueError: entries has the wrong length
sage: m=matrix(1,0,[]); m; m.parent()
[]
Full MatrixSpace of 1 by 0 dense matrices over Integer Ring
sage: m=matrix(0,1,[]); m; m.parent()
[]
Full MatrixSpace of 0 by 1 dense matrices over Integer Ring
sage: m=matrix(0,[]); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(0,{}); m; m.parent()
[]
Full MatrixSpace of 0 by 0 sparse matrices over Integer Ring
sage: m=matrix(0,{(1,1):2}); m; m.parent()
...
IndexError: invalid entries list
sage: m=matrix(2,0,{(1,1):2}); m; m.parent()
...
IndexError: invalid entries list
sage: import numpy
sage: n=numpy.array([[numpy.complex(0,1),numpy.complex(0,2)],[3,4]],complex)
sage: m=matrix(n); m; m.parent()
[1.0*I 2.0*I]
[  3.0   4.0]
Full MatrixSpace of 2 by 2 dense matrices over Complex Double Field
sage: n=numpy.array([[1,2],[3,4]],'int32')
sage: m=matrix(n); m; m.parent()
[1 2]
[3 4]
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: n = numpy.array([[1,2,3],[4,5,6],[7,8,9]],'float32')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Real Double Field
sage: n=numpy.array([[1,2,3],[4,5,6],[7,8,9]],'float64')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Real Double Field
sage: n=numpy.array([[1,2,3],[4,5,6],[7,8,9]],'complex64')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Complex Double Field
sage: n=numpy.array([[1,2,3],[4,5,6],[7,8,9]],'complex128')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Complex Double Field
sage: a = matrix([[1,2],[3,4]])
sage: b = matrix(a.numpy()); b
[1 2]
[3 4]
sage: a == b
True
sage: c = matrix(a.numpy('float32')); c
[1.0 2.0]
[3.0 4.0]
sage: matrix(numpy.array([[5]]))
[5]
sage: v = vector(ZZ, [1, 10, 100])
sage: m=matrix(ZZ['x'], v); m; m.parent()
[  1  10 100]
Full MatrixSpace of 1 by 3 dense matrices over Univariate Polynomial Ring in x over Integer Ring
sage: matrix(ZZ, 10, 10, range(100)).parent()
Full MatrixSpace of 10 by 10 dense matrices over Integer Ring
sage: m = matrix(GF(7), [[1/3,2/3,1/2], [3/4,4/5,7]]); m; m.parent()
[5 3 4]
[6 5 0]
Full MatrixSpace of 2 by 3 dense matrices over Finite Field of size 7
sage: m = matrix([[1,2,3], [RDF(2), CDF(1,2), 3]]); m; m.parent()
[        1.0         2.0         3.0]
[        2.0 1.0 + 2.0*I         3.0]
Full MatrixSpace of 2 by 3 dense matrices over Complex Double Field
sage: m=matrix(3,3,1/2); m; m.parent()
[1/2   0   0]
[  0 1/2   0]
[  0   0 1/2]
Full MatrixSpace of 3 by 3 dense matrices over Rational Field
sage: matrix([[1],[2,3]])
...
ValueError: List of rows is not valid (rows are wrong types or lengths)
sage: matrix([[1],2])
...
ValueError: List of rows is not valid (rows are wrong types or lengths)
sage: matrix(vector(RR,[1,2,3])).parent()
Full MatrixSpace of 1 by 3 dense matrices over Real Field with 53 bits of precision

AUTHORS:

??: Initial implementation
Jason Grout (2008-03): almost a complete rewrite, with bits and pieces from the original implementation

sage.matrix.constructor.block_diagonal_matrix(*sub_matrices, **kwds)¶

Create a block matrix whose diagonal block entries are given by sub_matrices, with zero elsewhere.

See also block_matrix.

EXAMPLES:

sage: A = matrix(ZZ, 2, [1,2,3,4])
sage: block_diagonal_matrix(A, A)
[1 2|0 0]
[3 4|0 0]
[---+---]
[0 0|1 2]
[0 0|3 4]

The sub-matrices need not be square:

sage: B = matrix(QQ, 2, 3, range(6))
sage: block_diagonal_matrix(~A, B)
[  -2    1|   0    0    0]
[ 3/2 -1/2|   0    0    0]
[---------+--------------]
[   0    0|   0    1    2]
[   0    0|   3    4    5]

sage.matrix.constructor.block_matrix(sub_matrices, nrows=None, ncols=None, subdivide=True)¶

Returns a larger matrix made by concatenating the sub_matrices (rows first, then columns). For example, the matrix

[ A B ]
[ C D ]

is made up of submatrices A, B, C, and D.

INPUT:

sub_matrices - matrices (must be of the correct size, or constants)
nrows - (optional) the number of block rows
ncols - (optional) the number of block cols
subdivide - boolean, whether or not to add subdivision information to the matrix

EXAMPLES:

sage: A = matrix(QQ, 2, 2, [3,9,6,10])
sage: block_matrix([A, -A, ~A, 100*A])
[    3     9|   -3    -9]
[    6    10|   -6   -10]
[-----------+-----------]
[-5/12   3/8|  300   900]
[  1/4  -1/8|  600  1000]

One can use constant entries:

sage: block_matrix([1, A, 0, 1])
[ 1  0| 3  9]
[ 0  1| 6 10]
[-----+-----]
[ 0  0| 1  0]
[ 0  0| 0  1]

A zero entry may represent any square or non-square zero matrix:

sage: B = matrix(QQ, 1, 1, [ 1 ] )
sage: C = matrix(QQ, 2, 2, [ 2, 3, 4, 5 ] )
sage: block_matrix([B, 0, 0, C])
[1|0 0]
[-+---]
[0|2 3]
[0|4 5]

One can specify the number of rows or columns (optional for square number of matrices):

sage: block_matrix([A, -A, ~A, 100*A], ncols=4)
[    3     9|   -3    -9|-5/12   3/8|  300   900]
[    6    10|   -6   -10|  1/4  -1/8|  600  1000]

sage: block_matrix([A, -A, ~A, 100*A], nrows=1)
[    3     9|   -3    -9|-5/12   3/8|  300   900]
[    6    10|   -6   -10|  1/4  -1/8|  600  1000]

It handle base rings nicely too:

sage: R.<x> = ZZ['x']
sage: block_matrix([1/2, A, 0, x-1])
[  1/2     0|    3     9]
[    0   1/2|    6    10]
[-----------+-----------]
[    0     0|x - 1     0]
[    0     0|    0 x - 1]
sage: block_matrix([1/2, A, 0, x-1]).parent()
Full MatrixSpace of 4 by 4 dense matrices over Univariate Polynomial Ring in x over Rational Field

Subdivisions are optional:

sage: B = matrix(QQ, 2, 3, range(6))
sage: block_matrix([~A, B, B, ~A], subdivide=False)
[-5/12   3/8     0     1     2]
[  1/4  -1/8     3     4     5]
[    0     1     2 -5/12   3/8]
[    3     4     5   1/4  -1/8]

sage.matrix.constructor.diagonal_matrix(arg0=None, arg1=None, arg2=None, sparse=None)¶

INPUT:

Supported formats

diagonal_matrix(diagonal_entries, [sparse=True]): diagonal matrix with flat list of entries
diagonal_matrix(nrows, diagonal_entries, [sparse=True]): diagonal matrix with flat list of entries and the rest zeros
diagonal_matrix(ring, diagonal_entries, [sparse=True]): diagonal matrix over specified ring with flat list of entries
diagonal_matrix(ring, nrows, diagonal_entries, [sparse=True]): diagonal matrix over specified ring with flat list of entries and the rest zeros
diagonal_matrix(vect, [sparse=True]): diagonal matrix with entries taken from a vector

The sparse option is optional, must be explicitly named (i.e., sparse=True), and may be either True or False.

EXAMPLES:

Input format 1:

sage: diagonal_matrix([1,2,3])
[1 0 0]
[0 2 0]
[0 0 3]

Input format 2:

sage: diagonal_matrix(3, [1,2])
[1 0 0]
[0 2 0]
[0 0 0]

Input format 3:

sage: diagonal_matrix(GF(3), [1,2,3])
[1 0 0]
[0 2 0]
[0 0 0]

Input format 4:

sage: diagonal_matrix(GF(3), 3, [8,2])
[2 0 0]
[0 2 0]
[0 0 0]

Input format 5:

sage: diagonal_matrix(vector(GF(3),[1,2,3]))
[1 0 0]
[0 2 0]
[0 0 0]

sage.matrix.constructor.identity_matrix(ring, n=0, sparse=False)¶

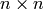Return the $n \times n$ identity matrix over the given ring.

The default ring is the integers.

EXAMPLES:

sage: M = identity_matrix(QQ, 2); M
[1 0]
[0 1]
sage: M.parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: M = identity_matrix(2); M
[1 0]
[0 1]
sage: M.parent()
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: M = identity_matrix(3, sparse=True); M
[1 0 0]
[0 1 0]
[0 0 1]
sage: M.parent()
Full MatrixSpace of 3 by 3 sparse matrices over Integer Ring

sage.matrix.constructor.jordan_block(eigenvalue, size, sparse=False)¶

Form the Jordan block with the specified size associated with the eigenvalue.

INPUT:

eigenvalue - eigenvalue for the diagonal entries of the block
size - size of the Jordan block
sparse - (default False) if True, return a sparse matrix

EXAMPLE:

sage: jordan_block(5, 3)
[5 1 0]
[0 5 1]
[0 0 5]

sage.matrix.constructor.matrix(*args, **kwds)¶

Create a matrix.

INPUT: The matrix command takes the entries of a matrix, optionally preceded by a ring and the dimensions of the matrix, and returns a matrix.

The entries of a matrix can be specified as a flat list of elements, a list of lists (i.e., a list of rows), a list of Sage vectors, a callable object, or a dictionary having positions as keys and matrix entries as values (see the examples). If you pass in a callable object, then you must specify the number of rows and columns. You can create a matrix of zeros by passing an empty list or the integer zero for the entries. To construct a multiple of the identity (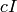 $cI$ ), you can specify square dimensions and pass in $c$ . Calling matrix() with a Sage object may return something that makes sense. Calling matrix() with a NumPy array will convert the array to a matrix.

The ring, number of rows, and number of columns of the matrix can be specified by setting the ring, nrows, or ncols parameters or by passing them as the first arguments to the function in the order ring, nrows, ncols. The ring defaults to ZZ if it is not specified or cannot be determined from the entries. If the numbers of rows and columns are not specified and cannot be determined, then an empty 0x0 matrix is returned.

ring - the base ring for the entries of the matrix.
nrows - the number of rows in the matrix.
ncols - the number of columns in the matrix.
sparse - create a sparse matrix. This defaults to True when the entries are given as a dictionary, otherwise defaults to False.

OUTPUT:

a matrix

EXAMPLES:

sage: m=matrix(2); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring

sage: m=matrix(2,3); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring

sage: m=matrix(QQ,[[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field

sage: m = matrix(QQ, 3, 3, lambda i, j: i+j); m
[0 1 2]
[1 2 3]
[2 3 4]
sage: m = matrix(3, lambda i,j: i-j); m
[ 0 -1 -2]
[ 1  0 -1]
[ 2  1  0]

sage: v1=vector((1,2,3))
sage: v2=vector((4,5,6))
sage: m=matrix([v1,v2]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring

sage: m=matrix(QQ,2,[1,2,3,4,5,6]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field

sage: m=matrix(QQ,2,3,[1,2,3,4,5,6]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field

sage: m=matrix({(0,1): 2, (1,1):2/5}); m; m.parent()
[  0   2]
[  0 2/5]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field

sage: m=matrix(QQ,2,3,{(1,1): 2}); m; m.parent()
[0 0 0]
[0 2 0]
Full MatrixSpace of 2 by 3 sparse matrices over Rational Field

sage: import numpy
sage: n=numpy.array([[1,2],[3,4]],float)
sage: m=matrix(n); m; m.parent()
[1.0 2.0]
[3.0 4.0]
Full MatrixSpace of 2 by 2 dense matrices over Real Double Field

sage: v = vector(ZZ, [1, 10, 100])
sage: m=matrix(v); m; m.parent()
[  1  10 100]
Full MatrixSpace of 1 by 3 dense matrices over Integer Ring
sage: m=matrix(GF(7), v); m; m.parent()
[1 3 2]
Full MatrixSpace of 1 by 3 dense matrices over Finite Field of size 7

sage: g = graphs.PetersenGraph()
sage: m = matrix(g); m; m.parent()
[0 1 0 0 1 1 0 0 0 0]
[1 0 1 0 0 0 1 0 0 0]
[0 1 0 1 0 0 0 1 0 0]
[0 0 1 0 1 0 0 0 1 0]
[1 0 0 1 0 0 0 0 0 1]
[1 0 0 0 0 0 0 1 1 0]
[0 1 0 0 0 0 0 0 1 1]
[0 0 1 0 0 1 0 0 0 1]
[0 0 0 1 0 1 1 0 0 0]
[0 0 0 0 1 0 1 1 0 0]
Full MatrixSpace of 10 by 10 dense matrices over Integer Ring

sage: matrix(ZZ, 10, 10, range(100), sparse=True).parent()
Full MatrixSpace of 10 by 10 sparse matrices over Integer Ring

sage: R = PolynomialRing(QQ, 9, 'x')
sage: A = matrix(R, 3, 3, R.gens()); A
[x0 x1 x2]
[x3 x4 x5]
[x6 x7 x8]
sage: det(A)
-x2*x4*x6 + x1*x5*x6 + x2*x3*x7 - x0*x5*x7 - x1*x3*x8 + x0*x4*x8

TESTS:

sage: m=matrix(); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(QQ); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Rational Field
sage: m=matrix(QQ,2); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: m=matrix(QQ,2,3); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix([]); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(QQ,[]); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Rational Field
sage: m=matrix(2,2,1); m; m.parent()
[1 0]
[0 1]
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: m=matrix(QQ,2,2,1); m; m.parent()
[1 0]
[0 1]
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: m=matrix(2,3,0); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring
sage: m=matrix(QQ,2,3,0); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix([[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring
sage: m=matrix(QQ,2,[[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix(QQ,3,[[1,2,3],[4,5,6]]); m; m.parent()
...
ValueError: Number of rows does not match up with specified number.
sage: m=matrix(QQ,2,3,[[1,2,3],[4,5,6]]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
sage: m=matrix(QQ,2,4,[[1,2,3],[4,5,6]]); m; m.parent()
...
ValueError: Number of columns does not match up with specified number.
sage: m=matrix([(1,2,3),(4,5,6)]); m; m.parent()
[1 2 3]
[4 5 6]
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring
sage: m=matrix([1,2,3,4,5,6]); m; m.parent()
[1 2 3 4 5 6]
Full MatrixSpace of 1 by 6 dense matrices over Integer Ring
sage: m=matrix((1,2,3,4,5,6)); m; m.parent()
[1 2 3 4 5 6]
Full MatrixSpace of 1 by 6 dense matrices over Integer Ring
sage: m=matrix(QQ,[1,2,3,4,5,6]); m; m.parent()
[1 2 3 4 5 6]
Full MatrixSpace of 1 by 6 dense matrices over Rational Field
sage: m=matrix(QQ,3,2,[1,2,3,4,5,6]); m; m.parent()
[1 2]
[3 4]
[5 6]
Full MatrixSpace of 3 by 2 dense matrices over Rational Field
sage: m=matrix(QQ,2,4,[1,2,3,4,5,6]); m; m.parent()
...
ValueError: entries has the wrong length
sage: m=matrix(QQ,5,[1,2,3,4,5,6]); m; m.parent()
...
TypeError: entries has the wrong length
sage: m=matrix({(1,1): 2}); m; m.parent()
[0 0]
[0 2]
Full MatrixSpace of 2 by 2 sparse matrices over Integer Ring
sage: m=matrix(QQ,{(1,1): 2}); m; m.parent()
[0 0]
[0 2]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: m=matrix(QQ,3,{(1,1): 2}); m; m.parent()
[0 0 0]
[0 2 0]
[0 0 0]
Full MatrixSpace of 3 by 3 sparse matrices over Rational Field
sage: m=matrix(QQ,3,4,{(1,1): 2}); m; m.parent()
[0 0 0 0]
[0 2 0 0]
[0 0 0 0]
Full MatrixSpace of 3 by 4 sparse matrices over Rational Field
sage: m=matrix(QQ,2,{(1,1): 2}); m; m.parent()
[0 0]
[0 2]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: m=matrix(QQ,1,{(1,1): 2}); m; m.parent()
...
IndexError: invalid entries list
sage: m=matrix({}); m; m.parent()
[]
Full MatrixSpace of 0 by 0 sparse matrices over Integer Ring
sage: m=matrix(QQ,{}); m; m.parent()
[]
Full MatrixSpace of 0 by 0 sparse matrices over Rational Field
sage: m=matrix(QQ,2,{}); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: m=matrix(QQ,2,3,{}); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 sparse matrices over Rational Field
sage: m=matrix(2,{}); m; m.parent()
[0 0]
[0 0]
Full MatrixSpace of 2 by 2 sparse matrices over Integer Ring
sage: m=matrix(2,3,{}); m; m.parent()
[0 0 0]
[0 0 0]
Full MatrixSpace of 2 by 3 sparse matrices over Integer Ring
sage: m=matrix(0); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(0,2); m; m.parent()
[]
Full MatrixSpace of 0 by 2 dense matrices over Integer Ring
sage: m=matrix(2,0); m; m.parent()
[]
Full MatrixSpace of 2 by 0 dense matrices over Integer Ring
sage: m=matrix(0,[1]); m; m.parent()
...
ValueError: entries has the wrong length
sage: m=matrix(1,0,[]); m; m.parent()
[]
Full MatrixSpace of 1 by 0 dense matrices over Integer Ring
sage: m=matrix(0,1,[]); m; m.parent()
[]
Full MatrixSpace of 0 by 1 dense matrices over Integer Ring
sage: m=matrix(0,[]); m; m.parent()
[]
Full MatrixSpace of 0 by 0 dense matrices over Integer Ring
sage: m=matrix(0,{}); m; m.parent()
[]
Full MatrixSpace of 0 by 0 sparse matrices over Integer Ring
sage: m=matrix(0,{(1,1):2}); m; m.parent()
...
IndexError: invalid entries list
sage: m=matrix(2,0,{(1,1):2}); m; m.parent()
...
IndexError: invalid entries list
sage: import numpy
sage: n=numpy.array([[numpy.complex(0,1),numpy.complex(0,2)],[3,4]],complex)
sage: m=matrix(n); m; m.parent()
[1.0*I 2.0*I]
[  3.0   4.0]
Full MatrixSpace of 2 by 2 dense matrices over Complex Double Field
sage: n=numpy.array([[1,2],[3,4]],'int32')
sage: m=matrix(n); m; m.parent()
[1 2]
[3 4]
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: n = numpy.array([[1,2,3],[4,5,6],[7,8,9]],'float32')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Real Double Field
sage: n=numpy.array([[1,2,3],[4,5,6],[7,8,9]],'float64')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Real Double Field
sage: n=numpy.array([[1,2,3],[4,5,6],[7,8,9]],'complex64')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Complex Double Field
sage: n=numpy.array([[1,2,3],[4,5,6],[7,8,9]],'complex128')
sage: m=matrix(n); m; m.parent()
[1.0 2.0 3.0]
[4.0 5.0 6.0]
[7.0 8.0 9.0]
Full MatrixSpace of 3 by 3 dense matrices over Complex Double Field
sage: a = matrix([[1,2],[3,4]])
sage: b = matrix(a.numpy()); b
[1 2]
[3 4]
sage: a == b
True
sage: c = matrix(a.numpy('float32')); c
[1.0 2.0]
[3.0 4.0]
sage: matrix(numpy.array([[5]]))
[5]
sage: v = vector(ZZ, [1, 10, 100])
sage: m=matrix(ZZ['x'], v); m; m.parent()
[  1  10 100]
Full MatrixSpace of 1 by 3 dense matrices over Univariate Polynomial Ring in x over Integer Ring
sage: matrix(ZZ, 10, 10, range(100)).parent()
Full MatrixSpace of 10 by 10 dense matrices over Integer Ring
sage: m = matrix(GF(7), [[1/3,2/3,1/2], [3/4,4/5,7]]); m; m.parent()
[5 3 4]
[6 5 0]
Full MatrixSpace of 2 by 3 dense matrices over Finite Field of size 7
sage: m = matrix([[1,2,3], [RDF(2), CDF(1,2), 3]]); m; m.parent()
[        1.0         2.0         3.0]
[        2.0 1.0 + 2.0*I         3.0]
Full MatrixSpace of 2 by 3 dense matrices over Complex Double Field
sage: m=matrix(3,3,1/2); m; m.parent()
[1/2   0   0]
[  0 1/2   0]
[  0   0 1/2]
Full MatrixSpace of 3 by 3 dense matrices over Rational Field
sage: matrix([[1],[2,3]])
...
ValueError: List of rows is not valid (rows are wrong types or lengths)
sage: matrix([[1],2])
...
ValueError: List of rows is not valid (rows are wrong types or lengths)
sage: matrix(vector(RR,[1,2,3])).parent()
Full MatrixSpace of 1 by 3 dense matrices over Real Field with 53 bits of precision

AUTHORS:

??: Initial implementation
Jason Grout (2008-03): almost a complete rewrite, with bits and pieces from the original implementation

sage.matrix.constructor.ncols_from_dict(d)¶

Given a dictionary that defines a sparse matrix, return the number of columns that matrix should have.

This is for internal use by the matrix function.

INPUT:

d - dict

OUTPUT:

integer

EXAMPLES:

sage: sage.matrix.constructor.ncols_from_dict({})
0

Here the answer is 301 not 300, since there is a 0-th row.

sage: sage.matrix.constructor.ncols_from_dict({(4,300):10})
301

sage.matrix.constructor.nrows_from_dict(d)¶

Given a dictionary that defines a sparse matrix, return the number of rows that matrix should have.

This is for internal use by the matrix function.

INPUT:

d - dict

OUTPUT:

integer

EXAMPLES:

sage: sage.matrix.constructor.nrows_from_dict({})
0

Here the answer is 301 not 300, since there is a 0-th row.

::: sage: sage.matrix.constructor.nrows_from_dict({(300,4):10}) 301

sage.matrix.constructor.prepare(w)¶

Given a list w of numbers, find a common ring that they all canonically map to, and return the list of images of the elements of w in that ring along with the ring.

This is for internal use by the matrix function.

INPUT:

w - list

OUTPUT:

list, ring

EXAMPLES:

sage: sage.matrix.constructor.prepare([-2, Mod(1,7)])
([5, 1], Ring of integers modulo 7)

Notice that the elements must all canonically coerce to a common ring (since Sequence is called):

sage: sage.matrix.constructor.prepare([2/1, Mod(1,7)])
...
TypeError: unable to find a common ring for all elements

sage.matrix.constructor.prepare_dict(w)¶

Given a dictionary w of numbers, find a common ring that they all canonically map to, and return the dictionary of images of the elements of w in that ring along with the ring.

This is for internal use by the matrix function.

INPUT:

w - dict

OUTPUT:

dict, ring

EXAMPLES:

sage: sage.matrix.constructor.prepare_dict({(0,1):2, (4,10):Mod(1,7)})
({(0, 1): 2, (4, 10): 1}, Ring of integers modulo 7)

sage.matrix.constructor.random_matrix(R, nrows, ncols=None, sparse=False, density=1, *args, **kwds)¶

Return a random matrix with entries in the ring R.

INPUT:

R - Ring
nrows - Integer; number of rows
ncols - (default: None); number of columns; if None defaults to nrows
sparse - (default: False); whether or not matrix is sparse
density - Integer (default: 1)
*args, **kwds - passed on to randomize function

EXAMPLES:

sage: A = random_matrix(ZZ,50,x=2^16)    # entries are up to 2^16 i size
sage: A
50 x 50 dense matrix over Integer Ring (type 'print A.str()' to see all of the entries)

sage.matrix.constructor.zero_matrix(ring, nrows, ncols=None, sparse=False)¶

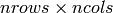Return the $nrows \times ncols$ zero matrix over the given ring.

The default ring is the integers.

EXAMPLES:

sage: M = zero_matrix(QQ, 2); M
[0 0]
[0 0]
sage: M.parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: M = zero_matrix(2, 3); M
[0 0 0]
[0 0 0]
sage: M.parent()
Full MatrixSpace of 2 by 3 dense matrices over Integer Ring
sage: M = zero_matrix(3, 1, sparse=True); M
[0]
[0]
[0]
sage: M.parent()
Full MatrixSpace of 3 by 1 sparse matrices over Integer Ring

Matrix Constructor.¶

Previous topic

Next topic

This Page

Navigation

Matrix Constructor.¶

Previous topic

Next topic

This Page

Quick search

Navigation