Interface to Octave

Octave is an open source MATLAB-like program with numerical routines for integrating, solving systems of equations, special functions, and solving (numerically) differential equations. Please see http://octave.sourceforge.net for more details.

The commands in this section only work if you have the optional “octave” interpreter installed and available in your PATH. It’s not necessary to install any special Sage packages.

EXAMPLES:

sage: octave.eval('2+2')    # optional -- requires Octave
'ans = 4'

sage: a = octave(10)        # optional -- requires Octave
sage: a**10                 # optional -- requires Octave
1e+10

LOG: - creation (William Stein) - ? (David Joyner, 2005-12-18) - Examples (David Joyner, 2005-01-03)

Computation of Special Functions

Octave implements computation of the following special functions (see the maxima and gp interfaces for even more special functions):

airy 
    Airy functions of the first and second kind, and their derivatives.
    airy(0,x) = Ai(x), airy(1,x) = Ai'(x), airy(2,x) = Bi(x), airy(3,x) = Bi'(x)
besselj
    Bessel functions of the first kind.
bessely
    Bessel functions of the second kind.
besseli
    Modified Bessel functions of the first kind.
besselk
    Modified Bessel functions of the second kind.
besselh
    Compute Hankel functions of the first (k = 1) or second (k = 2) kind.
beta 
    The Beta function,
          beta (a, b) = gamma (a) * gamma (b) / gamma (a + b).
betainc 
    The incomplete Beta function,
erf 
    The error function,
erfinv 
    The inverse of the error function. 
gamma 
    The Gamma function,
gammainc 
    The incomplete gamma function,

For example,

sage: octave("airy(3,2)")         # optional -- requires Octave
4.10068
sage: octave("beta(2,2)")         # optional -- requires Octave
0.166667
sage: octave("betainc(0.2,2,2)")  # optional -- requires Octave
0.104
sage: octave("besselh(0,2)")      # optional -- requires Octave
(0.223891,0.510376)
sage: octave("besselh(0,1)")      # optional -- requires Octave
(0.765198,0.088257)
sage: octave("besseli(1,2)")      # optional -- requires Octave
1.59064
sage: octave("besselj(1,2)")      # optional -- requires Octave
0.576725
sage: octave("besselk(1,2)")      # optional -- requires Octave
0.139866
sage: octave("erf(0)")            # optional -- requires Octave
0
sage: octave("erf(1)")            # optional -- requires Octave
0.842701
sage: octave("erfinv(0.842)")     # optional -- requires Octave
0.998315
sage: octave("gamma(1.5)")        # optional -- requires Octave
0.886227
sage: octave("gammainc(1.5,1)")   # optional -- requires Octave
0.77687

The Octave interface reads in even very long input (using files) in a robust manner:

sage: t = '"%s"'%10^10000   # ten thousand character string.
sage: a = octave.eval(t + ';')    # optional -- requires Octave, < 1/100th of a second
sage: a = octave(t)               # optional -- requires Octave

Note that actually reading a back out takes forever. This must be fixed ASAP - see http://trac.sagemath.org/sage_trac/ticket/940/.

Tutorial

EXAMPLES:

sage: octave('4+10')              # optional -- requires Octave
14
sage: octave('date')              # optional -- requires Octave; random output
18-Oct-2007
sage: octave('5*10 + 6')          # optional -- requires Octave
56
sage: octave('(6+6)/3')           # optional -- requires Octave
4
sage: octave('9')^2               # optional -- requires Octave
81
sage: a = octave(10); b = octave(20); c = octave(30)    # optional -- requires Octave
sage: avg = (a+b+c)/3             # optional -- requires Octave
sage: avg                         # optional -- requires Octave
20
sage: parent(avg)                 # optional -- requires Octave
Octave

sage: my_scalar = octave('3.1415')       # optional -- requires Octave
sage: my_scalar                          # optional -- requires Octave
3.1415
sage: my_vector1 = octave('[1,5,7]')     # optional -- requires Octave
sage: my_vector1                         # optional -- requires Octave
1     5     7
sage: my_vector2 = octave('[1;5;7]')     # optional -- requires Octave
sage: my_vector2                         # optional -- requires Octave
1
5
7
sage: my_vector1 * my_vector2            # optional -- requires Octave
75

class sage.interfaces.octave.Octave(maxread=100, script_subdirectory='', logfile=None, server=None, server_tmpdir=None)

Bases: sage.interfaces.expect.Expect

Interface to the Octave interpreter.

EXAMPLES:

sage: octave.eval("a = [ 1, 1, 2; 3, 5, 8; 13, 21, 33 ]")    # optional -- requires Octave
'a =\n\n 1 1 2\n 3 5 8\n 13 21 33\n\n'
sage: octave.eval("b = [ 1; 3; 13]")                         # optional -- requires Octave
'b =\n\n 1\n 3\n 13\n\n'
sage: octave.eval("c=a \\ b") # solves linear equation: a*c = b  # optional -- requires Octave; random output
'c =\n\n 1\n 7.21645e-16\n -7.21645e-16\n\n'
sage: octave.eval("c")                                 # optional -- requires Octave; random output
'c =\n\n 1\n 7.21645e-16\n -7.21645e-16\n\n'

clear(var)

Clear the variable named var.

EXAMPLES:

sage: octave.set('x', '2') #optional -- requires Octave
sage: octave.clear('x') #optional -- requires Octave
sage: octave.get('x') #optional -- requires Octave
"error: `x' undefined near line ... column 1"

console()

Spawn a new Octave command-line session.

This requires that the optional octave program be installed and in your PATH, but no optional Sage packages need be installed.

EXAMPLES:

sage: octave_console()         # not tested
GNU Octave, version 2.1.73 (i386-apple-darwin8.5.3).
Copyright (C) 2006 John W. Eaton.
...
octave:1> 2+3
ans = 5
octave:2> [ctl-d]

Pressing ctrl-d exits the octave console and returns you to Sage. octave, like Sage, remembers its history from one session to another.

de_system_plot(f, ics, trange)

Plots (using octave’s interface to gnuplot) the solution to a 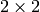system of differential equations.

INPUT:

• f - a pair of strings representing the differential equations; The independent variable must be called x and the dependent variable must be called y.
• ics - a pair [x0,y0] such that x(t0) = x0, y(t0) = y0
• trange - a pair [t0,t1]

OUTPUT: a gnuplot window appears

EXAMPLES:

sage: octave.de_system_plot(['x+y','x-y'], [1,-1], [0,2])  # not tested -- does this actually work (on OS X it fails for me -- William Stein, 2007-10)

This should yield the two plots 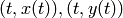on the same graph (the -axis is the horizontal axis) of the system of ODEs

get(var)

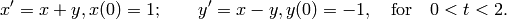
Get the value of the variable var.

EXAMPLES:

sage: octave.set('x', '2') #optional -- requires Octave
sage: octave.get('x') #optional -- requires Octave
' 2'

quit(verbose=False)

EXAMPLES:

sage: o = Octave()
sage: o._start()    #optional -- requires Octave
sage: o.quit(True)  #optional -- requires Octave
Exiting spawned Octave process.

sage2octave_matrix_string(A)

Return an octave matrix from a Sage matrix.

INPUT: A Sage matrix with entries in the rationals or reals.

OUTPUT: A string that evaluates to an Octave matrix.

EXAMPLES:

sage: M33 = MatrixSpace(QQ,3,3)
sage: A = M33([1,2,3,4,5,6,7,8,0])
sage: octave.sage2octave_matrix_string(A)   # optional -- requires Octave
'[1, 2, 3; 4, 5, 6; 7, 8, 0]'

AUTHORS:

• David Joyner and William Stein

set(var, value)

Set the variable var to the given value.

EXAMPLES:

sage: octave.set('x', '2') #optional -- requires Octave
sage: octave.get('x') #optional -- requires Octave
' 2'

solve_linear_system(A, b)

Use octave to compute a solution x to A*x = b, as a list.

INPUT:

• A - mxn matrix A with entries in QQ or RR
• b - m-vector b entries in QQ or RR (resp)

OUTPUT: An list x (if it exists) which solves M*x = b

EXAMPLES:

sage: M33 = MatrixSpace(QQ,3,3)
sage: A   = M33([1,2,3,4,5,6,7,8,0])
sage: V3  = VectorSpace(QQ,3)
sage: b   = V3([1,2,3])
sage: octave.solve_linear_system(A,b)    # optional -- requires Octave (and output is slightly random in low order bits)
[-0.33333299999999999, 0.66666700000000001, -3.5236600000000002e-18]

AUTHORS:

• David Joyner and William Stein

version()

Return the version of Octave.

OUTPUT: string

EXAMPLES:

sage: octave.version()   # optional -- requires Octave; random output depending on version
'2.1.73'

class sage.interfaces.octave.OctaveElement(parent, value, is_name=False, name=None)

Bases: sage.interfaces.expect.ExpectElement

sage.interfaces.octave.octave_console()

Spawn a new Octave command-line session.

This requires that the optional octave program be installed and in your PATH, but no optional Sage packages need be installed.

EXAMPLES:

sage: octave_console()         # not tested
GNU Octave, version 2.1.73 (i386-apple-darwin8.5.3).
Copyright (C) 2006 John W. Eaton.
...
octave:1> 2+3
ans = 5
octave:2> [ctl-d]

Pressing ctrl-d exits the octave console and returns you to Sage. octave, like Sage, remembers its history from one session to another.

sage.interfaces.octave.octave_version()

Return the version of Octave installed.

EXAMPLES:

sage: octave_version()    # optional -- requires Octave; and output is random
'2.9.12'

sage.interfaces.octave.reduce_load_Octave()

EXAMPLES:

sage: from sage.interfaces.octave import reduce_load_Octave
sage: reduce_load_Octave()
Octave