Sage provides an interface to the KASH computer algebra system, which is a free (as in beer!) but closed source program for algebraic number theory that shares much common code with Magma. To use KASH, you must install the appropriate optional Sage package by typing something like “sage -i kash3-linux-2005.11.22” or “sage -i kash3_osx-2005.11.22”. For a list of optional packages type “sage -optional”. If you type one of the above commands, the (about 16MB) package will be downloaded automatically (you don’t have to do that).
It is not enough to just have KASH installed on your computer. Note that the KASH Sage package is currently only available for Linux and OSX. If you need Windows, support contact me (wstein@gmail.com).
The KASH interface offers three pieces of functionality:
kash_console() - A function that dumps you into an interactive command-line KASH session. Alternatively,
type !kash from the Sage prompt.
kash(expr) - Creation of a Sage object that
wraps a KASH object. This provides a Pythonic interface to KASH.
For example, if f=kash.new(10), then
f.Factors() returns the prime factorization of
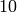computed using KASH.
kash.function_name(args ...) - Call the indicated KASH function with the given arguments are return the result as a KASH object.
kash.eval(expr) - Evaluation of arbitrary KASH expressions, with the result returned as a string.
For some reason hitting Control-C to interrupt a calculation doesn’t work correctly. (TODO)
The examples in this tutorial require that the optional kash package be installed.
Basic arithmetic is straightforward. First, we obtain the result as a string.
sage: kash.eval('(9 - 7) * (5 + 6)') # optional -- kash
'22'
Next we obtain the result as a new KASH object.
sage: a = kash('(9 - 7) * (5 + 6)'); a # optional -- kash
22
sage: a.parent() # optional -- kash
Kash
We can do arithmetic and call functions on KASH objects:
sage: a*a # optional -- kash
484
sage: a.Factorial() # optional -- kash
1124000727777607680000
Use the kash.help(name) command to get help about a given command. This returns a list of help for each of the definitions of name. Use print kash.help(name) to nicely print out all signatures.
Using the kash.new command we create Kash objects on which one can do arithmetic.
sage: a = kash(12345) # optional -- kash
sage: b = kash(25) # optional -- kash
sage: a/b # optional -- kash
2469/5
sage: a**b # optional -- kash
1937659030411463935651167391656422626577614411586152317674869233464019922771432158872187137603759765625
Variable assignment using kash is takes place in Sage.
sage: a = kash('32233') # optional -- kash
sage: a # optional -- kash
32233
In particular, a is not defined as part of the KASH session itself.
sage: kash.eval('a') # optional -- kash
"Error, the variable 'a' must have a value"
Use a.name() to get the name of the KASH variable:
sage: a.name() # somewhat random and optional - kash
'sage0'
sage: kash(a.name()) # optional -- kash
32233
We illustrate arithmetic with integers and rationals in KASH.
sage: F = kash.Factorization(4352) # optional -- kash
sage: F[1] # optional -- kash
<2, 8>
sage: F[2] # optional -- kash
<17, 1>
sage: F # optional -- kash
[ <2, 8>, <17, 1> ], extended by:
ext1 := 1,
ext2 := Unassign
Note
For some very large numbers KASH’s integer factorization seems much faster than PARI’s (which is the default in Sage).
sage: kash.GCD(15,25) # optional -- kash
5
sage: kash.LCM(15,25) # optional -- kash
75
sage: kash.Div(25,15) # optional -- kash
1
sage: kash(17) % kash(5) # optional -- kash
2
sage: kash.IsPrime(10007) # optional -- kash
TRUE
sage: kash.IsPrime(2005) # optional -- kash
FALSE
sage: kash.NextPrime(10007) # optional -- kash
10009
sage: kash.Precision() # optional -- kash
30
sage: kash('R') # optional -- kash
Real field of precision 30
sage: kash.Precision(40) # optional -- kash
40
sage: kash('R') # optional -- kash
Real field of precision 40
sage: z = kash('1 + 2*I') # optional -- kash
sage: z # optional -- kash
1.000000000000000000000000000000000000000 + 2.000000000000000000000000000000000000000*I
sage: z*z # optional -- kash
-3.000000000000000000000000000000000000000 + 4.000000000000000000000000000000000000000*I
sage: kash.Cos('1.24') # optional -- kash
0.3247962844387762365776934156973803996992
sage: kash('1.24').Cos() # optional -- kash
0.3247962844387762365776934156973803996992
sage: kash.Exp('1.24') # optional -- kash
3.455613464762675598057615494121998175400
sage: kash.Precision(30) # optional -- kash
30
sage: kash.Log('3+4*I') # optional -- kash
1.60943791243410037460075933323 + 0.927295218001612232428512462922*I
sage: kash.Log('I') # optional -- kash
1.57079632679489661923132169164*I
sage: kash.Sqrt(4) # optional -- kash
2.00000000000000000000000000000
sage: kash.Sqrt(2) # optional -- kash
1.41421356237309504880168872421
sage: kash.Floor('9/5') # optional -- kash
1
sage: kash.Floor('3/5') # optional -- kash
0
sage: x_c = kash('3+I') # optional -- kash
sage: x_c.Argument() # optional -- kash
0.321750554396642193401404614359
sage: x_c.Imaginary() # optional -- kash
1.00000000000000000000000000000
Note that list appends are completely different in KASH than in Python. Use underscore after the function name for the mutation version.
sage: v = kash([1,2,3]); v # optional -- kash
[ 1, 2, 3 ]
sage: v[1] # optional -- kash
1
sage: v[3] # optional -- kash
3
sage: v.Append([5]) # optional -- kash
[ 1, 2, 3, 5 ]
sage: v # optional -- kash
[ 1, 2, 3 ]
sage: v.Append_([5, 6]) # optional -- kash
SUCCESS
sage: v # optional -- kash
[ 1, 2, 3, 5, 6 ]
sage: v.Add(5) # optional -- kash
[ 1, 2, 3, 5, 6, 5 ]
sage: v # optional -- kash
[ 1, 2, 3, 5, 6 ]
sage: v.Add_(5) # optional -- kash
SUCCESS
sage: v # optional -- kash
[ 1, 2, 3, 5, 6, 5 ]
The Apply command applies a function to each element of a list.
the following are examples of ranges.
sage: L = kash('[1..10]') # optional -- kash
sage: L # optional -- kash
[ 1 .. 10 ]
sage: L = kash('[2,4..100]') # optional -- kash
sage: L # optional -- kash
[ 2, 4 .. 100 ]
sage: f = kash('X^3 + X + 1') # optional -- kash
sage: f + f # optional -- kash
2*X^3 + 2*X + 2
sage: f * f # optional -- kash
X^6 + 2*X^4 + 2*X^3 + X^2 + 2*X + 1
sage: f.Evaluate(10) # optional -- kash
1011
sage: Qx = kash.PolynomialAlgebra('Q') # optional -- kash
sage: Qx.gen(1)**5 + kash('7/3') # sage1 below somewhat random; optional -- kash
sage1.1^5 + 7/3
We create an equation order.
sage: f = kash('X^5 + 4*X^4 - 56*X^2 -16*X + 192') # optional -- kash
sage: OK = f.EquationOrder() # optional -- kash
sage: OK # optional -- kash
Equation Order with defining polynomial X^5 + 4*X^4 - 56*X^2 - 16*X + 192 over Z
sage: f = kash('X^5 + 4*X^4 - 56*X^2 -16*X + 192') # optional -- kash
sage: O = f.EquationOrder() # optional -- kash
sage: a = O.gen(2) # optional -- kash
sage: a # optional -- kash
[0, 1, 0, 0, 0]
sage: O.Basis() # output somewhat random; optional -- kash
[
_NG.1,
_NG.2,
_NG.3,
_NG.4,
_NG.5
]
sage: O.Discriminant() # optional -- kash
1364202618880
sage: O.MaximalOrder() # name sage2 below somewhat random; optional -- kash
Maximal Order of sage2
sage: O = kash.MaximalOrder('X^3 - 77') # optional -- kash
sage: I = O.Ideal(5,[2, 1, 0]) # optional -- kash
sage: I # name sage14 below random; optional -- kash
Ideal of sage14
Two element generators:
[5, 0, 0]
[2, 1, 0]
sage: F = I.Factorisation() # optional -- kash
sage: F # name sage14 random; optional -- kash
[
<Prime Ideal of sage14
Two element generators:
[5, 0, 0]
[2, 1, 0], 1>
]
Determining whether an ideal is principal.
sage: I.IsPrincipal() # optional -- kash
FALSE, extended by:
ext1 := Unassign
Computation of class groups and unit groups:
sage: f = kash('X^5 + 4*X^4 - 56*X^2 -16*X + 192') # optional -- kash
sage: O = kash.EquationOrder(f) # optional -- kash
sage: OK = O.MaximalOrder() # optional -- kash
sage: OK.ClassGroup() # name sage32 below random; optional -- kash
Abelian Group isomorphic to Z/6
Defined on 1 generator
Relations:
6*sage32.1 = 0, extended by:
ext1 := Mapping from: grp^abl: sage32 to ids/ord^num: _AA
sage: U = OK.UnitGroup() # optional -- kash
sage: U # name sage34 below random; optional -- kash
Abelian Group isomorphic to Z/2 + Z + Z
Defined on 3 generators
Relations:
2*sage34.1 = 0, extended by:
ext1 := Mapping from: grp^abl: sage34 to ord^num: sage30
sage: kash.Apply('x->%s.ext1(x)'%U.name(), U.Generators().List()) # optional -- kash
[ [1, -1, 0, 0, 0], [1, 1, 0, 0, 0], [-1, 0, 0, 0, 0] ]
sage: k = kash.FiniteField(25) # optional -- kash
sage: kT = k.RationalFunctionField() # optional -- kash
sage: kTy = kT.PolynomialAlgebra() # optional -- kash
sage: T = kT.gen(1) # optional -- kash
sage: y = kTy.gen(1) # optional -- kash
sage: f = y**3 + T**4 + 1 # optional -- kash
The KASH interface reads in even very long input (using files) in a robust manner, as long as you are creating a new object.
Note
Using kash.eval for long input is much less robust, and is not recommended.
sage: a = kash(range(10000)) # optional -- kash
Note that KASH seems to not support string or integer literals with more than 1024 digits, which is why the above example uses a list unlike for the other interfaces.
Bases: sage.interfaces.expect.Expect
Interface to the Kash interpreter.
AUTHORS:
Send the code in the string s to the Kash interpreter and return the output as a string.
INPUT:
Return help on KASH commands.
Returns help on all commands with a given name. If name is None, return the location of the installed Kash HTML documentation.
EXAMPLES:
sage: X = kash.help('IntegerRing') # optional -- kash
There is one entry in X for each item found in the documentation for this function: If you type print X[0] you will get help on about the first one, printed nicely to the screen.
AUTHORS: