Interface to Axiom¶

TODO:

Evaluation using a file is not done. Any input line with more than a few thousand characters would hang the system, so currently it automatically raises an exception.
All completions of a given command.
Interactive help.

Axiom is a free GPL-compatible (modified BSD license) general purpose computer algebra system whose development started in 1973 at IBM. It contains symbolic manipulation algorithms, as well as implementations of special functions, including elliptic functions and generalized hypergeometric functions. Moreover, Axiom has implementations of many functions relating to the invariant theory of the symmetric group 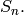$S_n.$ For many links to Axiom documentation see http://wiki.axiom-developer.org.

AUTHORS:

Bill Page (2006-10): Created this (based on Maxima interface)

Note

Bill Page put a huge amount of effort into the Sage Axiom interface over several days during the Sage Days 2 coding sprint. This is contribution is greatly appreciated.
William Stein (2006-10): misc touchup.
Bill Page (2007-08): Minor modifications to support axiom4sage-0.3

Note

The axiom4sage-0.3.spkg is based on an experimental version of the FriCAS fork of the Axiom project by Waldek Hebisch that uses pre-compiled cached Lisp code to build Axiom very quickly with clisp.

If the string “error” (case insensitive) occurs in the output of anything from axiom, a RuntimeError exception is raised.

EXAMPLES: We evaluate a very simple expression in axiom.

sage: axiom('3 * 5')                     #optional - axiom
15
sage: a = axiom(3) * axiom(5); a         #optional - axiom
15

The type of a is AxiomElement, i.e., an element of the axiom interpreter.

sage: type(a)                            #optional - axiom
<class 'sage.interfaces.axiom.AxiomElement'>
sage: parent(a)                          #optional - axiom
Axiom

The underlying Axiom type of a is also available, via the type method:

sage: a.type()                           #optional - axiom
PositiveInteger

We factor 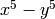$x^5 - y^5$ in Axiom in several different ways. The first way yields a Axiom object.

sage: F = axiom.factor('x^5 - y^5'); F      #optional - axiom
           4      3    2 2    3     4
- (y - x)(y  + x y  + x y  + x y + x )
sage: type(F)                               #optional - axiom
<class 'sage.interfaces.axiom.AxiomElement'>
sage: F.type()                              #optional - axiom
Factored Polynomial Integer

Note that Axiom objects are normally displayed using “ASCII art”.

sage: a = axiom(2/3); a          #optional - axiom
  2
  -
  3
sage: a = axiom('x^2 + 3/7'); a      #optional - axiom
   2   3
  x  + -
       7

The axiom.eval command evaluates an expression in axiom and returns the result as a string. This is exact as if we typed in the given line of code to axiom; the return value is what Axiom would print out.

sage: print axiom.eval('factor(x^5 - y^5)')   #optional - axiom
           4      3    2 2    3     4
- (y - x)(y  + x y  + x y  + x y + x )
Type: Factored Polynomial Integer

We can create the polynomial $f$ as a Axiom polynomial, then call the factor method on it. Notice that the notation f.factor() is consistent with how the rest of Sage works.

sage: f = axiom('x^5 - y^5')                  #optional - axiom
sage: f^2                                     #optional - axiom
   10     5 5    10
  y   - 2x y  + x
sage: f.factor()                              #optional - axiom
           4      3    2 2    3     4
- (y - x)(y  + x y  + x y  + x y + x )

Control-C interruption works well with the axiom interface, because of the excellent implementation of axiom. For example, try the following sum but with a much bigger range, and hit control-C.

sage:  f = axiom('(x^5 - y^5)^10000')       # not tested
Interrupting Axiom...
...
<type 'exceptions.TypeError'>: Ctrl-c pressed while running Axiom

sage: axiom('1/100 + 1/101')                  #optional - axiom
   201
  -----
  10100
sage: a = axiom('(1 + sqrt(2))^5'); a         #optional - axiom
     +-+
  29\|2  + 41

TESTS: We check to make sure the subst method works with keyword arguments.

sage: a = axiom(x+2); a  #optional - axiom
x + 2
sage: a.subst(x=3)       #optional - axiom
5

We verify that Axiom floating point numbers can be converted to Python floats.

sage: float(axiom(2))     #optional - axiom
2.0

class sage.interfaces.axiom.Axiom(name='axiom', command='axiom -nox -noclef', script_subdirectory=None, logfile=None, server=None, server_tmpdir=None, init_code=[, ')lisp (si::readline-off)'])¶

Bases: sage.interfaces.axiom.PanAxiom

console()¶

Spawn a new Axiom command-line session.

EXAMPLES:

sage: axiom.console() #not tested
                        AXIOM Computer Algebra System 
                        Version: Axiom (January 2009)
               Timestamp: Sunday January 25, 2009 at 07:08:54 
-----------------------------------------------------------------------------
   Issue )copyright to view copyright notices.
   Issue )summary for a summary of useful system commands.
   Issue )quit to leave AXIOM and return to shell.
-----------------------------------------------------------------------------

class sage.interfaces.axiom.AxiomElement(parent, value, is_name=False, name=None)¶: Bases: sage.interfaces.axiom.PanAxiomElement

class sage.interfaces.axiom.AxiomExpectFunction(parent, name)¶: Bases: sage.interfaces.axiom.PanAxiomExpectFunction

class sage.interfaces.axiom.AxiomFunctionElement(object, name)¶: Bases: sage.interfaces.axiom.PanAxiomFunctionElement

class sage.interfaces.axiom.PanAxiom(name='axiom', command='axiom -nox -noclef', script_subdirectory=None, logfile=None, server=None, server_tmpdir=None, init_code=[, ')lisp (si::readline-off)'])¶

Bases: sage.interfaces.expect.Expect

Interface to a PanAxiom interpreter.

get(var)¶

Get the string value of the Axiom variable var.

EXAMPLES:

sage: axiom.set('xx', '2')    #optional - axiom
sage: axiom.get('xx')         #optional - axiom
'2'
sage: a = axiom('(1 + sqrt(2))^5') #optional - axiom
sage: axiom.get(a.name())          #optional - axiom
'     +-+\r\r\n  29\\|2  + 41'

set(var, value)¶

Set the variable var to the given value.

EXAMPLES:

sage: axiom.set('xx', '2')    #optional - axiom
sage: axiom.get('xx')         #optional - axiom
'2'

sage: fricas.set('xx', '2')    #optional - fricas
sage: fricas.get('xx')         #optional - fricas
'2'

trait_names(verbose=True, use_disk_cache=True)¶

Returns a list of all the commands defined in Axiom and optionally (per default) store them to disk.

EXAMPLES:

sage: c = axiom.trait_names(use_disk_cache=False, verbose=False) #optional - axiom
sage: len(c) > 100  #optional - axiom
True
sage: 'factor' in c  #optional - axiom
True
sage: '**' in c     #optional - axiom
False
sage: 'upperCase?' in c  #optional - axiom
False
sage: 'upperCase_q' in c #optional - axiom
True
sage: 'upperCase_e' in c #optional - axiom
True

class sage.interfaces.axiom.PanAxiomElement(parent, value, is_name=False, name=None)¶

Bases: sage.interfaces.expect.ExpectElement

as_type(type)¶

Returns self as type.

EXAMPLES:

sage: a = axiom(1.2); a            #optional - axiom
1.2
sage: a.as_type(axiom.DoubleFloat) #optional - axiom
1.2
sage: _.type()                     #optional - axiom
DoubleFloat

sage: a = fricas(1.2); a            #optional - fricas
1.2
sage: a.as_type(fricas.DoubleFloat) #optional - fricas
1.2
sage: _.type()                      #optional - fricas
DoubleFloat

comma(*args)¶

Returns a Axiom tuple from self and args.

EXAMPLES:

sage: two = axiom(2)  #optional - axiom
sage: two.comma(3)    #optional - axiom
[2,3]
sage: two.comma(3,4)  #optional - axiom
[2,3,4]
sage: _.type()        #optional - axiom
Tuple PositiveInteger

sage: two = fricas(2)  #optional - fricas
sage: two.comma(3)     #optional - fricas
[2,3]
sage: two.comma(3,4)   #optional - fricas
[2,3,4]
sage: _.type()         #optional - fricas
Tuple(PositiveInteger)

type()¶

Returns the type of an AxiomElement.

EXAMPLES:

sage: axiom(x+2).type()  #optional - axiom
Polynomial Integer

unparsed_input_form()¶

Get the linear string representation of this object, if possible (often it isn’t).

EXAMPLES:

sage: a = axiom(x^2+1); a     #optional - axiom
   2
  x  + 1
sage: a.unparsed_input_form() #optional - axiom
'x*x+1'

sage: a = fricas(x^2+1)       #optional - fricas
sage: a.unparsed_input_form() #optional - fricas
'x^2+1'

class sage.interfaces.axiom.PanAxiomExpectFunction(parent, name)¶: Bases: sage.interfaces.expect.ExpectFunction

class sage.interfaces.axiom.PanAxiomFunctionElement(object, name)¶: Bases: sage.interfaces.expect.FunctionElement

sage.interfaces.axiom.axiom_console()¶

Spawn a new Axiom command-line session.

EXAMPLES:

sage: axiom_console() #not tested
                        AXIOM Computer Algebra System 
                        Version: Axiom (January 2009)
               Timestamp: Sunday January 25, 2009 at 07:08:54 
-----------------------------------------------------------------------------
   Issue )copyright to view copyright notices.
   Issue )summary for a summary of useful system commands.
   Issue )quit to leave AXIOM and return to shell.
-----------------------------------------------------------------------------

sage.interfaces.axiom.is_AxiomElement(x)¶

Returns True of x is of type AxiomElement.

EXAMPLES:

sage: from sage.interfaces.axiom import is_AxiomElement
sage: is_AxiomElement(axiom(2)) #optional - axiom
True
sage: is_AxiomElement(2)
False

sage.interfaces.axiom.reduce_load_Axiom()¶

Returns the Axiom interface object defined in sage.interfaces.axiom.

EXAMPLES:

sage: from sage.interfaces.axiom import reduce_load_Axiom
sage: reduce_load_Axiom()
Axiom

Interface to Axiom¶

Previous topic

Next topic

This Page

Navigation

Interface to Axiom¶

Previous topic

Next topic

This Page

Quick search

Navigation