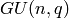Unitary Groups and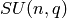

These are 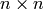unitary matrices with entries in .

AUTHORS:

• David Joyner (2006-03): initial version, modified from special_linear (by W. Stein)
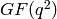• David Joyner (2006-05): minor additions (examples, _latex_, __str__, gens)
• William Stein (2006-12): rewrite

EXAMPLES:

sage: G = SU(3,GF(5))
sage: G.order()
378000
sage: G
Special Unitary Group of degree 3 over Finite Field of size 5
sage: G._gap_init_()
'SU(3, 5)'
sage: G.random_element()
[      1 4*a + 4 4*a + 1]
[2*a + 4 2*a + 1       0]
[      4     3*a 4*a + 2]
sage: G.base_ring()
Finite Field of size 5
sage: G.field_of_definition()
Finite Field in a of size 5^2

sage.groups.matrix_gps.unitary.GU(n, F, var='a')

Return the general unitary group of degree n over the finite field F.

INPUT:

• n - a positive integer
• F - finite field
• var - variable used to represent generator of quadratic extension of F, if needed.

EXAMPLES:

sage: G = GU(3,GF(7)); G
General Unitary Group of degree 3 over Finite Field of size 7
sage: G.gens()
[
[  a   0   0]
[  0   1   0]
[  0   0 5*a],
[6*a   6   1]
[  6   6   0]
[  1   0   0]
]
sage: G = GU(2,QQ)
...
NotImplementedError: general unitary group only implemented over finite fields

sage: G = GU(3,GF(5), var='beta')
sage: G.gens()
[
[  beta      0      0]
[     0      1      0]
[     0      0 3*beta],
[4*beta      4      1]
[     4      4      0]
[     1      0      0]
]

class sage.groups.matrix_gps.unitary.GeneralUnitaryGroup_finite_field(n, R, var='a', category=None)

Bases: sage.groups.matrix_gps.unitary.UnitaryGroup_finite_field

sage.groups.matrix_gps.unitary.SU(n, F, var='a')

Return the special unitary group of degree over .

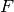EXAMPLES:

sage: SU(3,5)
Special Unitary Group of degree 3 over Finite Field of size 5
sage: SU(3,QQ)
...
NotImplementedError: special unitary group only implemented over finite fields

class sage.groups.matrix_gps.unitary.SpecialUnitaryGroup_finite_field(n, R, var='a', category=None)

Bases: sage.groups.matrix_gps.unitary.UnitaryGroup_finite_field

class sage.groups.matrix_gps.unitary.UnitaryGroup_finite_field(n, R, var='a', category=None)

Bases: sage.groups.matrix_gps.matrix_group.MatrixGroup_gap_finite_field

field_of_definition()

Return the field of definition of this general unity group.

EXAMPLES:

sage: G = GU(3,GF(5))
sage: G.field_of_definition()
Finite Field in a of size 5^2
sage: G.base_field()
Finite Field of size 5