Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Graph Theory »

This module implements PQ-Trees and methods to help recognise Interval Graphs.
Bases: sage.graphs.pq_trees.PQ
A P-Tree is a PQ-Tree whose children are not ordered (they can be permuted in any way)
Updates self so that its sets containing v are contiguous for any admissible permutation of its subtrees.
This function also ensures, whenever possible, that all the sets containing v are located on an interval on the right side of the ordering.
INPUT:
OUTPUT:
According to the cases :
- (EMPTY, ALIGNED) if no set of the tree contains an occurrence of v
- (FULL, ALIGNED) if all the sets of the tree contain v
- (PARTIAL, ALIGNED) if some (but not all) of the sets contain v, all of which are aligned to the right of the ordering at the end when the function ends
- (PARTIAL, UNALIGNED) if some (but not all) of the sets contain v, though it is impossible to align them all to the right
In any case, the sets containing v are contiguous when this function ends. If there is no possibility of doing so, the function raises a ValueError exception.
EXAMPLE:
Ensuring the sets containing 0 are continuous:
sage: from sage.graphs.pq_trees import P, Q
sage: p = P([[0,3], [1,2], [2,3], [2,4], [4,0],[2,8], [2,9]])
sage: p.set_contiguous(0)
(1, True)
sage: print p
('P', [{1, 2}, {2, 3}, {2, 4}, {8, 2}, {9, 2}, ('P', [{0, 3}, {0, 4}])])
Impossible situation:
sage: p = P([[0,1], [1,2], [2,3], [3,0]])
sage: p.set_contiguous(0)
(1, True)
sage: p.set_contiguous(1)
(1, True)
sage: p.set_contiguous(2)
(1, True)
sage: p.set_contiguous(3)
...
ValueError: Impossible
This class implements the PQ-Tree, used for the recognition of Interval Graphs, or equivalently for matrices having the so-caled “consecutive ones property”.
Briefly, we are given a collection 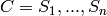 of sets on a
common ground set
of sets on a
common ground set  , and we would like to reorder the elements
of
, and we would like to reorder the elements
of  in such a way that for every element
in such a way that for every element 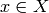 such that
such that
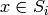 and
and 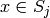 ,
, 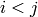 , we have
, we have 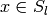 for all
for all
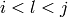 . This property could also be rephrased as : the sets
containing
. This property could also be rephrased as : the sets
containing 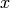 are an interval.
are an interval.
To achieve it, we will actually compute ALL the orderings satisfying such constraints using the structure of PQ-Tree, by adding the constraints one at a time.
At first, there is no constraint : all the permutations are allowed. We will then build a tree composed of one node linked to all the sets in our collection (his children). As we want to remember that all the permutations of his children are allowed, we will label it with “P”, making it a P-Tree.
We are now picking an element
, and we want to ensure that all the elements
containing it are contiguous. We can remove them from their tree
, create a second tree
whose only children are the
, and attach this
to
. We also make this new tree a
, as all the elements of
can be permuted as long as they stay close to each other. Obviously, the whole tree
can be prmuter with the other children of
in any way – it does not impair the fact that the sequence of the children will ensure the sets containing
are contiguous.
We would like to repeat the same procedure for
, but we are now encountering a problem : there may be sets containing both
and
, along with others containing only
or only
. We can permute the sets containing only
together, or the sets containing both
and
together, but we may NOT permute all the sets containing
together as this may break the relationship between the sets containing
. We need
-Trees. A
-Tree is a tree whose children are ordered, even though their order could be reversed (if the children of a
-Tree are
, we can change it to
). We can now express all the orderings satisfying our two constraints the following way :
We create a tree
gathering all the elements not containing
nor
, and make it a
We create 3
-Trees
, which respectively have for children the elements or our collection containing
- both
and
- only
- only
To ensure our constraints on both elements, we create a
-tree
whose children are in order
We now make this
-Tree
a children of the
-Tree
Using these two types of tree, and exploring the different cases of intersection, it is possible to represent all the possible permutations of our sets satisfying or constraints, or to prove that no such ordering exists. This is the whole purpose of this class and this algorithm, and is explained with more details in many places, for example in the following document from Hajiaghayi [Haj].
REFERENCES:
| [Haj] | M. Hajiaghayi http://www-math.mit.edu/~hajiagha/pp11.ps |
AUTHOR : Nathann Cohen
Returns the number of children of self
EXAMPLE:
sage: from sage.graphs.pq_trees import P, Q
sage: p = Q([[1,2], [2,3], P([[2,4], [2,8], [2,9]])])
sage: p.cardinality()
3
Returns a flattened copy of self
If self has only one child, we may as well consider its child’s children, as self encodes no information. This method recursively “flattens” trees having only on PQ-tree child, and returns it.
EXAMPLE:
sage: from sage.graphs.pq_trees import P, Q
sage: p = Q([P([[2,4], [2,8], [2,9]])])
sage: p.flatten()
('P', [{2, 4}, {8, 2}, {9, 2}])
Tests whether self is a 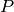 -Tree
-Tree
EXAMPLE:
sage: from sage.graphs.pq_trees import P, Q
sage: P([[0,1],[2,3]]).is_P()
True
sage: Q([[0,1],[2,3]]).is_P()
False
Tests whether self is a 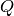 -Tree
-Tree
EXAMPLE:
sage: from sage.graphs.pq_trees import P, Q
sage: Q([[0,1],[2,3]]).is_Q()
True
sage: P([[0,1],[2,3]]).is_Q()
False
Returns the current ordering given by listing the leaves from left to right.
EXAMPLE:
sage: from sage.graphs.pq_trees import P, Q sage: p = Q([[1,2], [2,3], P([[2,4], [2,8], [2,9]])]) sage: p.ordering() [{1, 2}, {2, 3}, {2, 4}, {8, 2}, {9, 2}]
Recursively reverses self and its children
EXAMPLE:
sage: from sage.graphs.pq_trees import P, Q
sage: p = Q([[1,2], [2,3], P([[2,4], [2,8], [2,9]])])
sage: p.ordering()
[{1, 2}, {2, 3}, {2, 4}, {8, 2}, {9, 2}]
sage: p.reverse()
sage: p.ordering()
[{9, 2}, {8, 2}, {2, 4}, {2, 3}, {1, 2}]
Returns a simplified copy of self according to the element v
If self is a partial P-tree for v, we would like to
restrict the permutations of its children to permutations
keeping the children containing v contiguous. This
function also “locks” all the elements not containing v
inside a 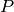 -tree, which is useful when one want to keep the
elements containing v on one side (which is the case when
this method is called).
-tree, which is useful when one want to keep the
elements containing v on one side (which is the case when
this method is called).
INPUT:
OUTPUT:
If self is a 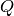 -Tree, the sequence of its children is
returned. If self is a
-Tree, the sequence of its children is
returned. If self is a 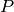 -tree, 2
-tree, 2 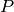 -tree are returned,
namely the two
-tree are returned,
namely the two 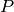 -tree defined above and restricting the
permutations, in the order implied by left, right (if
right =True, the second
-tree defined above and restricting the
permutations, in the order implied by left, right (if
right =True, the second 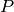 -tree will be the one gathering
the elements containing v, if left=True, the
opposite).
-tree will be the one gathering
the elements containing v, if left=True, the
opposite).
Note
This method is assumes that self is partial for v, and aligned to the side indicated by left, right.
EXAMPLES:
A 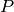 -Tree
-Tree
sage: from sage.graphs.pq_trees import P, Q
sage: p = P([[2,4], [1,2], [0,8], [0,5]])
sage: p.simplify(0, right = True)
[('P', [{2, 4}, {1, 2}]), ('P', [{0, 8}, {0, 5}])]
A 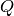 -Tree
-Tree
sage: q = Q([[2,4], [1,2], [0,8], [0,5]])
sage: q.simplify(0, right = True)
[{2, 4}, {1, 2}, {0, 8}, {0, 5}]
Returns the subsequences of children containing and not containing v
INPUT:
OUTPUT:
Two lists, the first containing the children of self containing v, and the other containing the other children.
Note
This command is meant to be used on a partial tree, once it has be “set continuous” on an element v and aligned it to the right. Hence, none of the list should be empty (an exception is raised if that happens, as it would reveal a bug in the algorithm) and the sum contains + does_not_contain should be equal to the sequence of children of self.
EXAMPLE:
sage: from sage.graphs.pq_trees import P, Q
sage: p = Q([[1,2], [2,3], P([[2,4], [2,8], [2,9]])])
sage: p.reverse()
sage: contains, does_not_contain = p.split(1)
sage: contains
[{1, 2}]
sage: does_not_contain
[('P', [{9, 2}, {8, 2}, {2, 4}]), {2, 3}]
sage: does_not_contain + contains == p._children
True
Bases: sage.graphs.pq_trees.PQ
A Q-Tree is a PQ-Tree whose children are ordered up to reversal
Updates self so that its sets containing v are contiguous for any admissible permutation of its subtrees.
This function also ensures, whenever possible, that all the sets containing v are located on an interval on the right side of the ordering.
INPUT:
OUTPUT:
According to the cases :
- (EMPTY, ALIGNED) if no set of the tree contains an occurrence of v
- (FULL, ALIGNED) if all the sets of the tree contain v
- (PARTIAL, ALIGNED) if some (but not all) of the sets contain v, all of which are aligned to the right of the ordering at the end when the function ends
- (PARTIAL, UNALIGNED) if some (but not all) of the sets contain v, though it is impossible to align them all to the right
In any case, the sets containing v are contiguous when this function ends. If there is no possibility of doing so, the function raises a ValueError exception.
EXAMPLE:
Ensuring the sets containing 0 are continuous:
sage: from sage.graphs.pq_trees import P, Q
sage: q = Q([[2,3], Q([[3,0],[3,1]]), Q([[4,0],[4,5]])])
sage: q.set_contiguous(0)
(1, False)
sage: print q
('Q', [{2, 3}, {1, 3}, {0, 3}, {0, 4}, {4, 5}])
Impossible situation:
sage: p = Q([[0,1], [1,2], [2,0]])
sage: p.set_contiguous(0)
...
ValueError: Impossible
Reorders a collection of sets such that each element appears on an interval.
Given a collection of sets 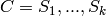 on a ground set
on a ground set  ,
this function attempts to reorder them in such a way that
,
this function attempts to reorder them in such a way that 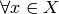 and
and 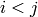 with
with 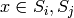 , then
, then 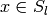 for every
for every
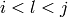 if it exists.
if it exists.
INPUT:
ALGORITHM:
PQ-Trees
EXAMPLE:
There is only one way (up to reversal) to represent contiguously
the sequence ofsets 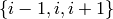 :
:
sage: from sage.graphs.pq_trees import reorder_sets
sage: seq = [Set([i-1,i,i+1]) for i in range(1,15)]
We apply a random permutation:
sage: p = Permutations(len(seq)).random_element()
sage: seq = [ seq[p(i+1)-1] for i in range(len(seq)) ]
sage: ordered = reorder_sets(seq)
sage: if not 0 in ordered[0]:
... ordered = ordered.reverse()
sage: print ordered
[{0, 1, 2}, {1, 2, 3}, {2, 3, 4}, {3, 4, 5}, {4, 5, 6}, {5, 6, 7}, {8, 6, 7}, {8, 9, 7}, {8, 9, 10}, {9, 10, 11}, {10, 11, 12}, {11, 12, 13}, {12, 13, 14}, {13, 14, 15}]