Fast sparse graphs

Usage Introduction

sage: from sage.graphs.base.sparse_graph import SparseGraph

Sparse graphs are initialized as follows:

sage: S = SparseGraph(nverts = 10, expected_degree = 3, extra_vertices = 10)

This example initializes a sparse graph with room for twenty vertices, the first ten of which are in the graph. In general, the first nverts are “active.” For example, see that 9 is already in the graph:

sage: S._num_verts()
10
sage: S.add_vertex(9)
9
sage: S._num_verts()
10

But 10 is not, until we add it:

sage: S._num_verts()
10
sage: S.add_vertex(10)
10
sage: S._num_verts()
11

You can begin working with unlabeled arcs right away as follows:

sage: S.add_arc(0,1)
sage: S.add_arc(1,2)
sage: S.add_arc(1,0)
sage: S.has_arc(7,3)
False
sage: S.has_arc(0,1)
True
sage: S.in_neighbors(1)
[0]
sage: S.out_neighbors(1)
[0, 2]
sage: S.del_all_arcs(0,1)
sage: S.all_arcs(0,1)
[]
sage: S.all_arcs(1,2)
[0]
sage: S.del_vertex(7)
sage: S.all_arcs(7,3)
...
RuntimeError: Vertex (7) is not a vertex of the graph.
sage: S._num_verts()
10
sage: S._num_arcs()
2

Sparse graphs support multiple edges and labeled edges, but requires that the labels be positive integers (the case label = 0 is treated as no label).

sage: S.add_arc_label(0,1,-1)
...
RuntimeError: Label (-1) must be a nonnegative integer.
sage: S.add_arc(0,1)
sage: S.arc_label(0,1)
0

Note that arc_label only returns the first edge label found in the specified place, and this can be in any order (if you want all arc labels, use all_arcs):

sage: S.add_arc_label(0,1,1)
sage: S.arc_label(0,1)
1
sage: S.all_arcs(0,1)
[0, 1]

Zero specifies only that there is no labeled arc:

sage: S.arc_label(1,2)
0

So do not be fooled:

sage: S.all_arcs(1,2)
[0]
sage: S.add_arc(1,2)
sage: S.arc_label(1,2)
0

Instead, if you work with unlabeled edges, be sure to use the right functions:

sage: T = SparseGraph(nverts = 3, expected_degree = 2)
sage: T.add_arc(0,1)
sage: T.add_arc(1,2)
sage: T.add_arc(2,0)
sage: T.has_arc(0,1)
True

Sparse graphs are by their nature directed. As of this writing, you need to do operations in pairs to treat the undirected case (or use a backend or a Sage graph):

sage: T.has_arc(1,0)
False

Multiple unlabeled edges are also possible:

sage: for _ in range(10): S.add_arc(5,4)
sage: S.all_arcs(5,4)
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

The curious developer is encouraged to check out the unsafe functions, which do not check input but which run in pure C.

Underlying Data Structure

The class SparseGraph contains the following variables which are inherited from CGraph (for explanation, refer to the documentation there):

cdef int num_verts
cdef int num_arcs
cdef int *in_degrees
cdef int *out_degrees
cdef bitset_t active_vertices

It also contains the following variables:

cdef int hash_length
cdef int hash_mask
cdef SparseGraphBTNode **vertices

For each vertex u, a hash table of length hash_length is instantiated. An arc (u, v) is stored at u * hash_length + hash(v) of the array vertices, where hash should be thought of as an arbitrary but fixed hash function which takes values in 0 <= hash < hash_length. Each address may represent different arcs, say (u, v1) and (u, v2) where hash(v1) == hash(v2). Thus, a binary tree structure is used at this step to speed access to individual arcs, whose nodes (each of which represents a pair (u,v)) are instances of the following type:

cdef struct SparseGraphBTNode:
    int vertex
    int number
    SparseGraphLLNode *labels
    SparseGraphBTNode *left
    SparseGraphBTNode *right

Which range of the vertices array the root of the tree is in determines u, and vertex stores v. The integer number stores only the number of unlabeled arcs from u to v.

Currently, labels are stored in a simple linked list, whose nodes are instances of the following type:

cdef struct SparseGraphLLNode:
    int label
    int number
    SparseGraphLLNode *next

The int label must be a positive integer, since 0 indicates no label, and negative numbers indicate errors. The int number is the number of arcs with the given label.

TODO: Optimally, edge labels would also be represented by a binary tree, which would help performance in graphs with many overlapping edges. Also, a more efficient binary tree structure could be used, although in practice the trees involved will usually have very small order, unless the degree of vertices becomes significantly larger than the expected_degree given, because this is the size of each hash table. Indeed, the expected size of the binary trees is 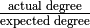. Ryan Dingman, e.g., is working on a general-purpose Cython-based red black tree, which would be optimal for both of these uses.

Methods

class sage.graphs.base.sparse_graph.SparseGraph

Bases: sage.graphs.base.c_graph.CGraph

Compiled sparse graphs.

sage: from sage.graphs.base.sparse_graph import SparseGraph

Sparse graphs are initialized as follows:

sage: S = SparseGraph(nverts = 10, expected_degree = 3, extra_vertices = 10)

INPUT:

• nverts - non-negative integer, the number of vertices.

• expected_degree - non-negative integer (default: 16), expected upper

  bound on degree of vertices.

• extra_vertices - non-negative integer (default: 0), how many extra

  vertices to allocate.

• verts - optional list of vertices to add

• arcs - optional list of arcs to add

The first nverts are created as vertices of the graph, and the next extra_vertices can be freely added without reallocation. See top level documentation for more details. The input verts and arcs are mainly for use in pickling.

add_arc(u, v)

Adds arc (u, v) to the graph with no label.

INPUT:

• u, v – non-negative integers, must be in self

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc(0,1)
sage: G.add_arc(4,7)
...
RuntimeError: Vertex (7) is not a vertex of the graph.
sage: G.has_arc(1,0)
False
sage: G.has_arc(0,1)
True

add_arc_label(u, v, l=0)

Adds arc (u, v) to the graph with label l.

INPUT:

• u, v - non-negative integers, must be in self
• l - a positive integer label, or zero for no label

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc_label(0,1)
sage: G.add_arc_label(4,7)
...
RuntimeError: Vertex (7) is not a vertex of the graph.
sage: G.has_arc(1,0)
False
sage: G.has_arc(0,1)
True
sage: G.add_arc_label(1,2,2)
sage: G.arc_label(1,2)
2

all_arcs(u, v)

Gives the labels of all arcs (u, v). An unlabeled arc is interpreted as having label 0.

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc_label(1,2,1)
sage: G.add_arc_label(1,2,2)
sage: G.add_arc_label(1,2,2)
sage: G.add_arc_label(1,2,2)
sage: G.add_arc_label(1,2,3)
sage: G.add_arc_label(1,2,3)
sage: G.add_arc_label(1,2,4)
sage: G.all_arcs(1,2)
[4, 3, 3, 2, 2, 2, 1]

arc_label(u, v)

Retrieves the first label found associated with (u, v).

INPUT:

• u, v - non-negative integers, must be in self

OUTPUT:

• positive integer - indicates that there is a label on (u, v).
• 0 - either the arc (u, v) is unlabeled, or there is no arc at all.

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc_label(3,4,7)
sage: G.arc_label(3,4)
7

NOTES:

To this function, an unlabeled arc is indistinguishable from a non-arc:

sage: G.add_arc_label(1,0)
sage: G.arc_label(1,0)
0
sage: G.arc_label(1,1)
0

This function only returns the first label it finds from u to v:

sage: G.add_arc_label(1,2,1)
sage: G.add_arc_label(1,2,2)
sage: G.arc_label(1,2)
2

del_all_arcs(u, v)

Deletes all arcs from u to v.

INPUT:

• u, v - integers

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc_label(0,1,0)
sage: G.add_arc_label(0,1,1)
sage: G.add_arc_label(0,1,2)
sage: G.add_arc_label(0,1,3)
sage: G.del_all_arcs(0,1)
sage: G.has_arc(0,1)
False
sage: G.arc_label(0,1)
0
sage: G.del_all_arcs(0,1)

del_arc_label(u, v, l)

Delete an arc (u, v) with label l.

INPUT:

• u, v - non-negative integers, must be in self
• l - a positive integer label, or zero for no label

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc_label(0,1,0)
sage: G.add_arc_label(0,1,1)
sage: G.add_arc_label(0,1,2)
sage: G.add_arc_label(0,1,2)
sage: G.add_arc_label(0,1,3)
sage: G.del_arc_label(0,1,2)
sage: G.all_arcs(0,1)
[0, 3, 2, 1]
sage: G.del_arc_label(0,1,0)
sage: G.all_arcs(0,1)
[3, 2, 1]

has_arc(u, v)

Checks whether arc (u, v) is in the graph.

INPUT:

• u, v - integers

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc_label(0,1)
sage: G.has_arc(1,0)
False
sage: G.has_arc(0,1)
True

has_arc_label(u, v, l)

Indicates whether there is an arc (u, v) with label l.

INPUT:

• u, v – non-negative integers, must be in self
• l – a positive integer label, or zero for no label

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc_label(0,1,0)
sage: G.add_arc_label(0,1,1)
sage: G.add_arc_label(0,1,2)
sage: G.add_arc_label(0,1,2)
sage: G.has_arc_label(0,1,1)
True
sage: G.has_arc_label(0,1,2)
True
sage: G.has_arc_label(0,1,3)
False

in_neighbors(v)

Gives all u such that (u, v) is an arc of the graph.

INPUT:

• v - integer

EXAMPLES:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc(0,1)
sage: G.add_arc(3,1)
sage: G.add_arc(1,3)
sage: G.in_neighbors(1)
[0, 3]
sage: G.in_neighbors(3)
[1]

out_neighbors(u)

Gives all v such that (u, v) is an arc of the graph.

INPUT:

• u - integer

EXAMPLES:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: G = SparseGraph(5)
sage: G.add_arc(0,1)
sage: G.add_arc(1,2)
sage: G.add_arc(1,3)
sage: G.out_neighbors(0)
[1]
sage: G.out_neighbors(1)
[2, 3]

realloc(total)

Reallocate the number of vertices to use, without actually adding any.

INPUT:

• total - integer, the total size to make the array

Returns -1 and fails if reallocation would destroy any active vertices.

EXAMPLES:

sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: S = SparseGraph(nverts=4, extra_vertices=4)
sage: S.current_allocation()
8
sage: S.add_vertex(6)
6
sage: S.current_allocation()
8
sage: S.add_vertex(10)
10
sage: S.current_allocation()
16
sage: S.add_vertex(40)
...
RuntimeError: Requested vertex is past twice the allocated range: use realloc.
sage: S.realloc(50)
sage: S.add_vertex(40)
40
sage: S.current_allocation()
50
sage: S.realloc(30)
-1
sage: S.current_allocation()
50
sage: S.del_vertex(40)
sage: S.realloc(30)
sage: S.current_allocation()
30

class sage.graphs.base.sparse_graph.SparseGraphBackend

Bases: sage.graphs.base.c_graph.CGraphBackend

Backend for Sage graphs using SparseGraphs.

sage: from sage.graphs.base.sparse_graph import SparseGraphBackend

This class is only intended for use by the Sage Graph and DiGraph class. If you are interested in using a SparseGraph, you probably want to do something like the following example, which creates a Sage Graph instance which wraps a SparseGraph object:

sage: G = Graph(30, implementation="c_graph", sparse=True)
sage: G.add_edges([(0,1), (0,3), (4,5), (9, 23)])
sage: G.edges(labels=False)
[(0, 1), (0, 3), (4, 5), (9, 23)]

Note that Sage graphs using the backend are more flexible than SparseGraphs themselves. This is because SparseGraphs (by design) do not deal with Python objects:

sage: G.add_vertex((0,1,2))
sage: G.vertices()
[0,
...
 29,
 (0, 1, 2)]
sage: from sage.graphs.base.sparse_graph import SparseGraph
sage: SG = SparseGraph(30)
sage: SG.add_vertex((0,1,2))
...
TypeError: an integer is required

add_edge(u, v, l, directed)

Adds the edge (u,v) to self.

INPUT:

• u,v - the vertices of the edge
• l - the edge label
• directed - if False, also add (v,u)

EXAMPLE:

sage: D = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: D.add_edge(0,1,None,False)
sage: list(D.iterator_edges(range(9), True))
[(0, 1, None)]

add_edges(edges, directed)

Add edges from a list.

INPUT:

• edges - the edges to be added - can either be of the form (u,v) or (u,v,l)
• directed - if False, add (v,u) as well as (u,v)

EXAMPLE:

sage: D = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: D.add_edges([(0,1), (2,3), (4,5), (5,6)], False)
sage: list(D.iterator_edges(range(9), True))
[(0, 1, None),
 (2, 3, None),
 (4, 5, None),
 (5, 6, None)]

del_edge(u, v, l, directed)

Delete edge (u,v,l).

INPUT:

• u,v - the vertices of the edge
• l - the edge label
• directed - if False, also delete (v,u,l)

EXAMPLE:

sage: D = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: D.add_edges([(0,1), (2,3), (4,5), (5,6)], False)
sage: list(D.iterator_edges(range(9), True))
[(0, 1, None),
 (2, 3, None),
 (4, 5, None),
 (5, 6, None)]
sage: D.del_edge(0,1,None,True)
sage: list(D.iterator_out_edges(range(9), True))
[(1, 0, None),
 (2, 3, None),
 (3, 2, None),
 (4, 5, None),
 (5, 4, None),
 (5, 6, None),
 (6, 5, None)]

get_edge_label(u, v)

Returns the edge label for (u,v).

INPUT:

• u,v - the vertices of the edge

EXAMPLE:

sage: D = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: D.add_edges([(0,1,1), (2,3,2), (4,5,3), (5,6,2)], False)
sage: list(D.iterator_edges(range(9), True))
[(0, 1, 1), (2, 3, 2), (4, 5, 3), (5, 6, 2)]
sage: D.del_edge(0,1,None,True) # "None" is equivalent to not providing a label
sage: list(D.iterator_edges(range(9), True))
[(2, 3, 2), (4, 5, 3), (5, 6, 2)]
sage: D.get_edge_label(3,2)
2

has_edge(u, v, l)

Returns whether this graph has edge (u,v) with label l. If l is None, return whether this graph has an edge (u,v) with any label.

INPUT:

• u,v - the vertices of the edge
• l - the edge label, or None

EXAMPLE:

sage: D = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: D.add_edges([(0,1), (2,3), (4,5), (5,6)], False)
sage: D.has_edge(0,1,None)
True

iterator_edges(vertices, labels)

Iterate over the edges incident to a sequence of vertices. Edges are assumed to be undirected.

INPUT:

• vertices - a list of vertex labels
• labels - boolean, whether to return labels as well

EXAMPLE:

sage: G = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: G.add_edge(1,2,3,False)
sage: list(G.iterator_edges(range(9), False))
[(1, 2)]
sage: list(G.iterator_edges(range(9), True))
[(1, 2, 3)]

iterator_in_edges(vertices, labels)

Iterate over the incoming edges incident to a sequence of vertices.

INPUT:

• vertices - a list of vertex labels
• labels - boolean, whether to return labels as well

EXAMPLE:

sage: G = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: G.add_edge(1,2,3,True)
sage: list(G.iterator_in_edges([1], False))
[]
sage: list(G.iterator_in_edges([2], False))
[(1, 2)]
sage: list(G.iterator_in_edges([2], True))
[(1, 2, 3)]

iterator_out_edges(vertices, labels)

Iterate over the outbound edges incident to a sequence of vertices.

INPUT:

• vertices - a list of vertex labels
• labels - boolean, whether to return labels as well

EXAMPLE:

sage: G = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: G.add_edge(1,2,3,True)
sage: list(G.iterator_out_edges([2], False))
[]
sage: list(G.iterator_out_edges([1], False))
[(1, 2)]
sage: list(G.iterator_out_edges([1], True))
[(1, 2, 3)]

multiple_edges(new)

Get/set whether or not self allows multiple edges.

INPUT:

• new - boolean (to set) or None (to get)

EXAMPLES:

sage: G = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: G.multiple_edges(True)
sage: G.multiple_edges(None)
True
sage: G.multiple_edges(False)
sage: G.multiple_edges(None)
False
sage: G.add_edge(0,1,0,True)
sage: G.add_edge(0,1,0,True)
sage: list(G.iterator_edges(range(9), True))
[(0, 1, 0)]

set_edge_label(u, v, l, directed)

Label the edge (u,v) by l.

INPUT:

• u,v - the vertices of the edge
• l - the edge label
• directed - if False, also set (v,u) with label l

EXAMPLE:

sage: G = sage.graphs.base.sparse_graph.SparseGraphBackend(9)
sage: G.add_edge(1,2,0,None)
sage: G.set_edge_label(1,2,'a',True)
sage: list(G.iterator_edges(range(9), True))
[(1, 2, 'a')]

Note that it fails silently if there is no edge there:

sage: G.set_edge_label(2,1,'b',True)
sage: list(G.iterator_edges(range(9), True))
[(1, 2, 'a')]

class sage.graphs.base.sparse_graph.id_dict

This is a helper class for pickling sparse graphs. It emulates a dictionary d which contains all objects, and always, d[x] == x.

EXAMPLE:

sage: from sage.graphs.base.sparse_graph import id_dict
sage: d = id_dict()
sage: d[None] is None
True
sage: d[7]
7
sage: d[{}]
{}
sage: d[()]
()

sage.graphs.base.sparse_graph.random_stress()

Randomly search for mistakes in the code.

DOCTEST (No output indicates that no errors were found):

sage: from sage.graphs.base.sparse_graph import random_stress
sage: for _ in xrange(20):
...    random_stress()