This module contains functions for computing with exact (rational) or floating-point convex polyhedra in arbitrary dimensions. The bulk of this functionality is provided through the cddlib library of Komei Fukuda.
There seems to be some inconsistency in the use of the word polyhedra. In this module, a polyhedron is a convex (possibly unbounded) set in Euclidean space cut out by a finite set of linear inequalities and linear equations. Note that the dimension of the polyhedron can be less than the dimension of the ambient space. There are two complementary representations of the same data:
This describes a polyhedron as the common solution set of a finite number of
- linear inequalities
, and
- linear equations
.
The other representation is as the convex hull of vertices (and rays and lines to all for unbounded polyhedra) as generators. The polyhedron is then the Minkowski sum
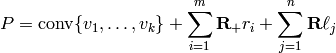
where
,
,
are a finite number of vertices,
,
,
are generators of rays,
- and
,
,
are generators of full lines.
A polytope is defined as a bounded polyhedron.
EXAMPLES:
sage: trunc_quadr = Polyhedron(vertices=[[1,0],[0,1]], rays=[[1,0],[0,1]])
sage: trunc_quadr
A 2-dimensional polyhedron in QQ^2 defined as the convex hull of 2 vertices and 2 rays.
sage: v = trunc_quadr.vertex_generator().next() # the first vertex in the internal enumeration
sage: v
A vertex at (1, 0)
sage: v()
(1, 0)
sage: list(v)
[1, 0]
sage: len(v)
2
sage: v[0] + v[1]
1
sage: v.is_vertex()
True
sage: type(v)
<class 'sage.geometry.polyhedra.Vertex'>
sage: type( v() )
<type 'sage.modules.vector_rational_dense.Vector_rational_dense'>
sage: v.polyhedron()
A 2-dimensional polyhedron in QQ^2 defined as the convex hull of 2 vertices and 2 rays.
sage: r = trunc_quadr.ray_generator().next()
sage: r
A ray in the direction (1, 0)
sage: r()
(1, 0)
sage: [x for x in v.neighbors()]
[A ray in the direction (1, 0), A vertex at (0, 1)]
Inequalities 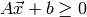 (and, similarly, equations) are specified by a list [b, A]:
(and, similarly, equations) are specified by a list [b, A]:
sage: Polyhedron(ieqs = [[0,1,0],[0,0,1],[1,-1,-1]]).Hrepresentation()
[An inequality (1, 0) x + 0 >= 0, An inequality (0, 1) x + 0 >= 0, An inequality (-1, -1) x + 1 >= 0]
REFERENCES:
Komei Fukuda’s FAQ in Polyhedral Computation
AUTHORS:
- Marshall Hampton: first version, bug fixes, and various improvements, 2008 and 2009
- Arnaud Bergeron: improvements to triangulation and rendering, 2008
- Sebastien Barthelemy: documentation improvements, 2008
- Volker Braun: refactoring, handle non-compact case, 2009
TESTS:
TestSuite(s).run()
Bases: sage.geometry.polyhedra.Hrepresentation
A linear equation of the polyhedron. That is, the polyhedron is strictly smaller-dimensional than the ambient space, and contained in this hyperplane. Inherits from Hrepresentation.
Tests whether the hyperplane defined by the equation contains the given vertex/ray/line.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0,0],[1,1,0],[1,2,0]])
sage: v = p.vertex_generator().next()
sage: v
A vertex at (0, 0, 0)
sage: a = p.equation_generator().next()
sage: a
An equation (0, 0, 1) x + 0 == 0
sage: a.contains(v)
True
Tests whether the interior of the halfspace (excluding its boundary) defined by the inequality contains the given vertex/ray/line.
NOTE:
Returns False for any equation.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0,0],[1,1,0],[1,2,0]])
sage: v = p.vertex_generator().next()
sage: v
A vertex at (0, 0, 0)
sage: a = p.equation_generator().next()
sage: a
An equation (0, 0, 1) x + 0 == 0
sage: a.interior_contains(v)
False
Tests if this object is an equation. By construction, it must be.
TESTS:
sage: p = Polyhedron(vertices = [[0,0,0],[1,1,0],[1,2,0]])
sage: a = p.equation_generator().next()
sage: a.is_equation()
True
Bases: sage.geometry.polyhedra.PolyhedronRepresentation
The internal base class for H-representation objects of a polyhedron. Inherits from PolyhedronRepresentation.
Returns the coefficient vector 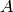 in
in  .
.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,1,0],[0,0,1],[1,-1,0,],[1,0,-1]])
sage: pH = p.Hrepresentation(0)
sage: pH.A()
(1, 0)
Alias for neighbors().
TESTS:
sage: p = Polyhedron(ieqs = [[0,0,0,2],[0,0,1,0,],[0,10,0,0],[1,-1,0,0],[1,0,-1,0,],[1,0,0,-1]])
sage: pH = p.Hrepresentation(0)
sage: a = list(pH.neighbors())
sage: b = list(pH.adjacent())
sage: a==b
True
Returns the constant 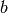 in
in 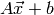 .
.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,1,0],[0,0,1],[1,-1,0,],[1,0,-1]])
sage: pH = p.Hrepresentation(0)
sage: pH.b()
0
Evaluates the left hand side 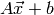 on the given
vertex/ray/line.
on the given
vertex/ray/line.
NOTES:
- Evaluating on a vertex returns
- Evaluating on a ray returns
. Only the sign or whether it is zero is meaningful.
- Evaluating on a line returns
. Only whether it is zero or not is meaningful.
EXAMPLES:
sage: triangle = Polyhedron(vertices=[[1,0],[0,1],[-1,-1]])
sage: ineq = triangle.inequality_generator().next()
sage: ineq
An inequality (-1, -1) x + 1 >= 0
sage: [ ineq.eval(v) for v in triangle.vertex_generator() ]
[0, 0, 3]
sage: [ ineq * v for v in triangle.vertex_generator() ]
[0, 0, 3]
If you pass a vector, it is assumed to be the coordinate vector of a point:
sage: ineq.eval( vector(ZZ, [3,2]) )
-4
Returns a generator for the incident H-representation objects, that is, the vertices/rays/lines satisfying the (in)equality.
EXAMPLES:
sage: triangle = Polyhedron(vertices=[[1,0],[0,1],[-1,-1]])
sage: ineq = triangle.inequality_generator().next()
sage: ineq
An inequality (-1, -1) x + 1 >= 0
sage: [ v for v in ineq.incident()]
[A vertex at (1, 0), A vertex at (0, 1)]
sage: p = Polyhedron(vertices=[[0,0,0],[0,1,0],[0,0,1]], rays=[[1,-1,-1]])
sage: ineq = p.Hrepresentation(2)
sage: ineq
An inequality (1, 1, 0) x + 0 >= 0
sage: [ x for x in ineq.incident() ]
[A ray in the direction (1, -1, -1),
A vertex at (0, 0, 0),
A vertex at (0, 0, 1)]
Returns True if the object is part of a H-representation (inequality or equation).
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,1,0],[0,0,1],[1,-1,0,],[1,0,-1]])
sage: pH = p.Hrepresentation(0)
sage: pH.is_H()
True
Returns True if the object is an equation of the H-representation.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,1,0],[0,0,1],[1,-1,0,],[1,0,-1]], eqns = [[1,1,-1]])
sage: pH = p.Hrepresentation(0)
sage: pH.is_equation()
True
Returns whether the incidence matrix element (Vobj,self) == 1
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,0,0,1],[0,0,1,0,],[0,1,0,0],[1,-1,0,0],[1,0,-1,0,],[1,0,0,-1]])
sage: pH = p.Hrepresentation(0)
sage: pH.is_incident(p.Vrepresentation(1))
True
sage: pH.is_incident(p.Vrepresentation(5))
False
Returns True if the object is an inequality of the H-representation.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,1,0],[0,0,1],[1,-1,0,],[1,0,-1]])
sage: pH = p.Hrepresentation(0)
sage: pH.is_inequality()
True
Iterate over the adjacent facets (i.e. inequalities/equations)
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,0,0,1],[0,0,1,0,],[0,1,0,0],[1,-1,0,0],[1,0,-1,0,],[1,0,0,-1]])
sage: pH = p.Hrepresentation(0)
sage: a = list(pH.neighbors())
sage: a[0]
An inequality (0, 1, 0) x + 0 >= 0
sage: list(a[0])
[0, 0, 1, 0]
Bases: sage.geometry.polyhedra.Hrepresentation
A linear inequality (supporting hyperplane) of the polyhedron. Inherits from Hrepresentation.
Tests whether the halfspace (including its boundary) defined by the inequality contains the given vertex/ray/line.
EXAMPLES:
sage: p = polytopes.cross_polytope(3)
sage: i1 = p.inequality_generator().next()
sage: [i1.contains(q) for q in p.vertex_generator()]
[True, True, True, True, True, True]
sage: p2 = 3*polytopes.n_cube(3)
sage: [i1.contains(q) for q in p2.vertex_generator()]
[True, False, True, True, False, False, True, False]
Tests whether the interior of the halfspace (excluding its boundary) defined by the inequality contains the given vertex/ray/line.
EXAMPLES:
sage: p = polytopes.cross_polytope(3)
sage: i1 = p.inequality_generator().next()
sage: [i1.interior_contains(q) for q in p.vertex_generator()]
[True, False, True, False, True, False]
sage: p2 = 3*polytopes.n_cube(3)
sage: [i1.interior_contains(q) for q in p2.vertex_generator()]
[True, False, True, True, False, False, True, False]
If you pass a vector, it is assumed to be the coordinate vector of a point:
sage: P = Polyhedron(vertices=[[1,1],[1,-1],[-1,1],[-1,-1]])
sage: p = vector(ZZ, [1,0] )
sage: [ ieq.interior_contains(p) for ieq in P.inequality_generator() ]
[True, True, True, False]
Returns True since this is, by construction, an inequality.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0,0],[1,1,0],[1,2,0]])
sage: a = p.inequality_generator().next()
sage: a.is_inequality()
True
Bases: sage.geometry.polyhedra.Vrepresentation
A line (Minkowski summand 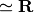 ) of the
polyhedron. Inherits from Vrepresentation.
) of the
polyhedron. Inherits from Vrepresentation.
Returns 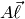
EXAMPLES:
sage: p = Polyhedron(ieqs = [[1, 0, 0, 1],[1,1,0,0]])
sage: a = p.line_generator().next()
sage: h = p.inequality_generator().next()
sage: a.evaluated_on(h)
0
Tests if the object is a line. By construction it must be.
TESTS:
sage: p = Polyhedron(ieqs = [[1, 0, 0, 1],[1,1,0,0]])
sage: a = p.line_generator().next()
sage: a.is_line()
True
Bases: sage.structure.sage_object.SageObject
A class for polyhedral objects. You may either instantiate with vertex/ray/line or inequalities/equations data, but not both. Redundant data will automatically be removed, and the complementary representation will be computed.
EXAMPLES:
Construct some polyhedra:
sage: square_from_vertices = Polyhedron(vertices = [[1, 1], [1, -1], [-1, 1], [-1, -1]])
sage: square_from_ieqs = Polyhedron(ieqs = [[1, 0, 1], [1, 1, 0], [1, 0, -1], [1, -1, 0]])
sage: list(square_from_ieqs.vertex_generator())
[A vertex at (1, -1),
A vertex at (1, 1),
A vertex at (-1, 1),
A vertex at (-1, -1)]
sage: list(square_from_vertices.inequality_generator())
[An inequality (0, 1) x + 1 >= 0,
An inequality (1, 0) x + 1 >= 0,
An inequality (0, -1) x + 1 >= 0,
An inequality (-1, 0) x + 1 >= 0]
sage: p = Polyhedron(vertices = [[1.1, 2.2], [3.3, 4.4]], field=RDF)
sage: p.n_inequalities()
2
The same polyhedron given in two ways:
sage: p = Polyhedron(ieqs = [[0,1,0,0],[0,0,1,0]])
sage: p.Vrepresentation()
[A line in the direction (0, 0, 1),
A ray in the direction (1, 0, 0),
A ray in the direction (0, 1, 0),
A vertex at (0, 0, 0)]
sage: q = Polyhedron(vertices=[[0,0,0]], rays=[[1,0,0],[0,1,0]], lines=[[0,0,1]])
sage: q.Hrepresentation()
[An inequality (1, 0, 0) x + 0 >= 0,
An inequality (0, 1, 0) x + 0 >= 0]
Finally, a more complicated example. Take 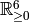 with
coordinates
with
coordinates 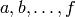 and
and
- The inequality
- The inequality
- The equation
sage: positive_coords = Polyhedron(ieqs=[[0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 0, 1]])
sage: P = Polyhedron(ieqs=positive_coords.inequalities() + [[0,0,1,-1,-1,1,0], [0,0,-1,1,-1,1,0]], eqns=[[-31,1,1,1,1,1,1]])
sage: P
A 5-dimensional polyhedron in QQ^6 defined as the convex hull of 7 vertices.
sage: P.dim()
5
sage: P.Vrepresentation()
[A vertex at (0, 31/2, 31/2, 0, 0, 0), A vertex at (0, 31/2, 0, 0, 31/2, 0), A vertex at (0, 0, 0, 0, 31, 0), A vertex at (0, 0, 31/2, 0, 31/2, 0), A vertex at (0, 0, 0, 31/2, 31/2, 0), A vertex at (31, 0, 0, 0, 0, 0), A vertex at (0, 0, 0, 0, 0, 31)]
Finally, a more complicated example. Take 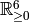 with
coordinates
with
coordinates 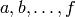 and
and
- The inequality
- The inequality
- The equation
sage: positive_coords = Polyhedron(ieqs=[[0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 0, 1]])
sage: P = Polyhedron(ieqs=positive_coords.inequalities() + [[0,0,1,-1,-1,1,0], [0,0,-1,1,-1,1,0]], eqns=[[-31,1,1,1,1,1,1]])
sage: P
A 5-dimensional polyhedron in QQ^6 defined as the convex hull of 7 vertices.
sage: P.dim()
5
sage: P.Vrepresentation()
[A vertex at (0, 31/2, 31/2, 0, 0, 0), A vertex at (0, 31/2, 0, 0, 31/2, 0), A vertex at (0, 0, 0, 0, 31, 0), A vertex at (0, 0, 31/2, 0, 31/2, 0), A vertex at (0, 0, 0, 31/2, 31/2, 0), A vertex at (31, 0, 0, 0, 0, 0), A vertex at (0, 0, 0, 0, 0, 31)]
NOTES:
- Once constructed, a Polyhedron object is immutable.
- Although the option field = RDF allows numerical data to be used, it might not give the right answer for degenerate input data - the results can depend upon the tolerance setting of cddlib.
Returns an iterator over the objects of the H-representation (inequalities or equations).
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: p.Hrep_generator().next()
An inequality (0, 0, 1) x + 1 >= 0
Returns the objects of the H-representaton. Each entry is either an inequality or a equation.
INPUT:
The optional argument is an index in 0...n_Hrepresentations(). Without an argument, returns the list of all H-representation objects.
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: p.Hrepresentation(0)
An inequality (0, 0, 1) x + 1 >= 0
sage: p.Hrepresentation(0) == p.Hrepresentation() [0]
True
Returns an iterator over the objects of the V-representation (vertices, rays, and lines).
EXAMPLES:
sage: p = polytopes.cyclic_polytope(3,4)
sage: vg = p.Vrep_generator()
sage: vg.next()
A vertex at (0, 0, 0)
sage: vg.next()
A vertex at (1, 1, 1)
Returns the objects of the V-representation. Each entry is either a vertex, a ray, or a line.
INPUT:
The optional argument is an index in 0...n_Hrepresentations(). Without an argument, returns the list of all H-representation objects.
EXAMPLES:
sage: p = polytopes.n_simplex(4)
sage: p.Vrepresentation(0)
A vertex at (0, 0, 0, -44721/50000)
sage: p.Vrepresentation(0) == p.Vrepresentation() [0]
True
This is an alias for vertex_adjacency_matrix()
EXAMPLES:
sage: polytopes.n_cube(3).adjacency_matrix()
[0 1 1 0 1 0 0 0]
[1 0 0 1 0 1 0 0]
[1 0 0 1 0 0 1 0]
[0 1 1 0 0 0 0 1]
[1 0 0 0 0 1 1 0]
[0 1 0 0 1 0 0 1]
[0 0 1 0 1 0 0 1]
[0 0 0 1 0 1 1 0]
Returns the dimension of the ambient space.
EXAMPLES:
sage: poly_test = Polyhedron(vertices = [[1,0,0,0],[0,1,0,0]])
sage: poly_test.ambient_dim()
4
Returns a polyhedron that is a bipyramid over the original.
EXAMPLES:
sage: octahedron = polytopes.cross_polytope(3)
sage: cross_poly_4d = octahedron.bipyramid()
sage: cross_poly_4d.n_vertices()
8
sage: q = [list(v) for v in cross_poly_4d.vertex_generator()]
sage: q
[[0, 0, 0, 1],
[0, 0, 1, 0],
[0, 1, 0, 0],
[0, 0, 0, -1],
[0, 0, -1, 0],
[0, -1, 0, 0],
[1, 0, 0, 0],
[-1, 0, 0, 0]]
Now check that bipyramids of cross-polytopes are cross-polytopes:
sage: q2 = [list(v) for v in polytopes.cross_polytope(4).vertex_generator()]
sage: [v in q2 for v in q]
[True, True, True, True, True, True, True, True]
Returns the bounded edges (excluding rays and lines).
OUTPUT:
A generator for pairs of vertices, one pair per edge.
EXAMPLES:
sage: p = Polyhedron(vertices=[[1,0],[0,1]], rays=[[1,0],[0,1]])
sage: [ e for e in p.bounded_edges() ]
[[A vertex at (1, 0), A vertex at (0, 1)]]
sage: for e in p.bounded_edges(): print e
[A vertex at (1, 0), A vertex at (0, 1)]
Writes the inequalities/equations data of the polyhedron in cdd’s H-representation format.
OUTPUT:
A string. If you save the output to filename.ine then you can run the stand-alone cdd via cddr+ filename.ine
EXAMPLES:
sage: p = polytopes.n_cube(2)
sage: print p.cdd_Hrepresentation()
H-representation
begin
4 3 rational
1 0 1
1 1 0
1 0 -1
1 -1 0
end
Writes the vertices/rays/lines data of the polyhedron in cdd’s V-representation format.
OUTPUT:
A string. If you save the output to filename.ext then you can run the stand-alone cdd via cddr+ filename.ext
EXAMPLES:
sage: q = Polyhedron(vertices = [[1,1],[0,0],[1,0],[0,1]])
sage: print q.cdd_Vrepresentation()
V-representation
begin
4 3 rational
1 1 1
1 0 0
1 1 0
1 0 1
end
Returns the average of the vertices. Returns the origin for the empty polytope. All rays and lines are ignored.
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: p = p + vector([1,0,0])
sage: p.center()
(1, 0, 0)
Return the common field for both self and other.
INPUT:
The argument other must be either:
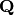 or
or 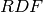
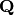 or
or 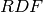
OUTPUT:
Either 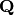 or
or 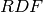 . Raises TypeError if other is not a
suitable input.
. Raises TypeError if other is not a
suitable input.
Note
“Real” numbers in sage are not necessarily elements of
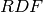 . For example, the literal
. For example, the literal 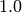 is not.
is not.
EXAMPLES:
sage: triangle_QQ = Polyhedron(vertices = [[1,0],[0,1],[1,1]], field=QQ)
sage: triangle_RDF = Polyhedron(vertices = [[1,0],[0,1],[1,1]], field=RDF)
sage: triangle_QQ.coerce_field(QQ)
Rational Field
sage: triangle_QQ.coerce_field(triangle_RDF)
Real Double Field
sage: triangle_RDF.coerce_field(triangle_QQ)
Real Double Field
sage: triangle_QQ.coerce_field(RDF)
Real Double Field
sage: triangle_QQ.coerce_field(ZZ)
Rational Field
sage: triangle_QQ.coerce_field(1/2)
Rational Field
sage: triangle_QQ.coerce_field(0.5)
Real Double Field
Returns whether the polyhedron contains the given point. See also Polyhedron.interior_contains(point).
EXAMPLES:
sage: P = Polyhedron(vertices=[[1,1],[1,-1],[0,0]])
sage: P.contains( [1,0] )
True
sage: P.contains( P.center() ) # true for any convex set
True
Returns the convex hull of the set-theoretic union of the two polyhedra.
EXAMPLES:
sage: a_simplex = polytopes.n_simplex(3)
sage: verts = a_simplex.vertices()
sage: verts = [[x[0]*3/5+x[1]*4/5, -x[0]*4/5+x[1]*3/5, x[2]] for x in verts]
sage: another_simplex = Polyhedron(vertices = verts)
sage: simplex_union = a_simplex.convex_hull(another_simplex)
sage: simplex_union.n_vertices()
7
Returns the dimension of the polyhedron.
EXAMPLES:
sage: simplex = Polyhedron(vertices = [[1,0,0,0],[0,0,0,1],[0,1,0,0],[0,0,1,0]])
sage: simplex.dim()
3
sage: simplex.ambient_dim()
4
Returns a new polyhedron formed from two points on each edge between two vertices.
INPUT:
- cut_frac - how deeply to cut into the edge. Default is
.
OUTPUT:
A Polyhedron object, truncated as described above.
EXAMPLES:
Truncating a cube:
sage: cube = polytopes.n_cube(3)
sage: trunc_cube = cube.edge_truncation()
sage: trunc_cube.n_vertices()
24
sage: trunc_cube.n_inequalities()
14
Returns a generator for the linear equations satisfied by the polyhedron.
EXAMPLES:
sage: p = polytopes.regular_polygon(8,field=RDF)
sage: p3 = Polyhedron(vertices = [x+[0] for x in p.vertices()], field=RDF)
sage: p3.equation_generator().next()
An equation (0.0, 0.0, 1.0) x + 0.0 == 0
Returns the linear constraints of the polyhedron. As with inequalities, each constraint is given as [b -a1 -a2 ... an] where for variables x1, x2,..., xn, the polyhedron satisfies the equation b = a1*x1 + a2*x2 + ... + an*xn.
NOTES:
It is recommended to use equation_generator() instead to iterate over the list of Equation objects.
EXAMPLES:
sage: test_p = Polyhedron(vertices = [[1,2,3,4],[2,1,3,4],[4,3,2,1],[3,4,1,2]])
sage: test_p.equations()
[[-10, 1, 1, 1, 1]]
Returns the f-vector (number of faces in each dimension) of the polytope as a list.
EXAMPLES:
sage: p = Polyhedron(vertices = [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1], [0, 0, 0]])
sage: p.f_vector()
[1, 7, 12, 7, 1]
Computes the face-lattice poset. Elements are tuples of (vertices, facets) - i.e. this keeps track of both the vertices in each face, and all the facets containing them.
EXAMPLES:
sage: c5_10 = Polyhedron(vertices = [[i,i^2,i^3,i^4,i^5] for i in range(1,11)])
sage: c5_10_fl = c5_10.face_lattice()
sage: [len(x) for x in c5_10_fl.level_sets()]
[1, 10, 45, 100, 105, 42, 1]
TESTS:
sage: c5_20 = Polyhedron(vertices = [[i,i^2,i^3,i^4,i^5] for i in range(1,21)]) # not tested - very long time
sage: c5_20_fl = c5_20.face_lattice() # not tested - very long time
sage: [len(x) for x in c5_20_fl.level_sets()] # not tested - very long time
[1, 20, 190, 580, 680, 272, 1]
sage: polytopes.n_cube(2).face_lattice().plot()
sage: level_sets = polytopes.cross_polytope(2).face_lattice().level_sets()
sage: print level_sets[0], level_sets[-1]
[(None, (0, 1, 2, 3))] [((0, 1, 2, 3), None)]
REFERENCES:
‘Computing the Face Lattice of a Polytope from its Vertex-Facet Incidences’, by V. Kaibel and M.E. Pfetsch.
Returns the adjacency matrix for the facets and hyperplanes.
EXAMPLES:
sage: polytopes.n_simplex(4).facet_adjacency_matrix()
[0 1 1 1 1]
[1 0 1 1 1]
[1 1 0 1 1]
[1 1 1 0 1]
[1 1 1 1 0]
Returns a list of face indices (i.e. indices of H-representation objects) and the indices of faces adjacent to them.
NOTES:
Instead of working with face indices, you can use the H-representation objects directly (see example).
EXAMPLES:
sage: p = polytopes.permutahedron(4)
sage: p.facial_adjacencies()[0:3]
[[0, [1, 2, 12, 13]], [1, [0, 2, 3, 6, 8, 13]], [2, [0, 1, 3, 4, 7, 12]]]
sage: f0 = p.Hrepresentation(0)
sage: f0.index() == 0
True
sage: f0_adjacencies = [f0.index(), [n.index() for n in f0.neighbors()]]
sage: p.facial_adjacencies()[0] == f0_adjacencies
True
Returns the face-vertex incidences in the form ![[f_i, [v_{i_0}, v_{i_1},\dots ,v_{i_2}]]](../../_images/math/dd3a1f5054f8981ac65d632db594cc969a6f96bc.png) .
.
NOTES:
Instead of working with face/vertex indices, you can use the H-representation/V-representation objects directly (see examples).
OUTPUT:
The face indices are the indices of the H-representation objects, and the vertex indices are the indices of the V-representation objects.
EXAMPLES:
sage: p = Polyhedron(vertices = [[5,0,0],[0,5,0],[5,5,0],[0,0,0],[2,2,5]])
sage: p.facial_incidences()
[[0, [1, 3, 4]],
[1, [0, 3, 4]],
[2, [0, 2, 4]],
[3, [1, 2, 4]],
[4, [0, 1, 2, 3]]]
sage: f0 = p.Hrepresentation(0)
sage: f0.index() == 0
True
sage: f0_incidences = [f0.index(), [v.index() for v in f0.incident()]]
sage: p.facial_incidences()[0] == f0_incidences
True
Return the number type that we are working with, either QQ (exact arithmetic using gmp, default) or RDF (double precision floating-point arithmetic)
EXAMPLES:
sage: triangle = Polyhedron(vertices = [[1,0],[0,1],[1,1]])
sage: triangle.field() == QQ
True
Returns the Gale transform of a polytope as described in the reference below.
OUTPUT:
A list of vectors, the Gale transform. The dimension is the dimension of the affine dependencies of the vertices of the polytope.
EXAMPLES:
This is from the reference, for a triangular prism:
sage: p = Polyhedron(vertices = [[0,0],[0,1],[1,0]])
sage: p2 = p.prism()
sage: p2.gale_transform()
[(1, 0), (0, 1), (-1, -1), (-1, 0), (0, -1), (1, 1)]
REFERENCES:
Lectures in Geometric Combinatorics, R.R.Thomas, 2006, AMS Press.
Returns a graph in which the vertices correspond to vertices of the polyhedron, and edges to edges.
OUTPUT:
A graph
EXAMPLES:
sage: g3 = polytopes.n_cube(3).graph()
sage: len(g3.automorphism_group())
48
sage: s4 = polytopes.n_simplex(4).graph()
sage: s4.is_eulerian()
True
Deprecated. Alias for inequalities()
EXAMPLES:
sage: p3 = Polyhedron(vertices = permutations([1,2,3,4]))
sage: p3.ieqs() == p3.inequalities()
True
Returns the incidence matrix.
NOTES:
The columns correspond to inequalities/equations in the order self.Hrepresentation(), the rowns correspond to vertices/rays/lines in the order self.Vrepresentation()
EXAMPLES:
sage: p = polytopes.cuboctahedron()
sage: p.incidence_matrix()
[0 0 1 0 0 1 0 0 1 1 0 0 0 0]
[0 0 0 1 0 0 0 0 0 1 1 0 1 0]
[0 1 1 0 0 0 0 0 1 0 0 0 0 1]
[0 0 0 0 0 0 0 0 0 0 1 1 1 1]
[1 1 0 0 0 0 0 0 0 0 0 1 0 1]
[0 0 0 0 0 0 0 0 1 1 1 0 0 1]
[1 0 0 0 0 0 0 1 0 0 0 1 1 0]
[1 1 1 0 0 0 1 0 0 0 0 0 0 0]
[1 0 0 0 1 0 1 1 0 0 0 0 0 0]
[0 0 0 1 1 0 0 1 0 0 0 0 1 0]
[0 0 0 1 1 1 0 0 0 1 0 0 0 0]
[0 0 1 0 1 1 1 0 0 0 0 0 0 0]
sage: v = p.Vrepresentation(0)
sage: v
A vertex at (0, -1/2, -1/2)
sage: h = p.Hrepresentation(2)
sage: h
An inequality (0, 2, 0) x + 1 >= 0
sage: h.eval(v) # evaluation (0, 2, 0) * (0, -1/2, -1/2) + 1
0
sage: h*v # same as h.eval(v)
0
sage: p.incidence_matrix() [0,2] # this entry is (v,h)
1
sage: h.contains(v)
True
sage: p.incidence_matrix() [2,0] # note: not symmetric
0
Returns a list of inequalities as coefficient lists.
NOTES:
It is recommended to use inequality_generator() instead to iterate over the list of Inequality objects.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0,0],[0,0,1],[0,1,0],[1,0,0],[2,2,2]])
sage: p.inequalities()[0:3]
[[0, 0, 0, 1], [0, 0, 1, 0], [0, 1, 0, 0]]
sage: p3 = Polyhedron(vertices = permutations([1,2,3,4]))
sage: ieqs = p3.inequalities()
sage: ieqs[0]
[-1, 0, 0, 1, 0]
sage: ieqs[-1]
[4, -1, 0, 0, 0]
sage: ieqs == [list(x) for x in p3.inequality_generator()]
True
Returns a generator for the defining inequalities of the polyhedron.
OUTPUT:
A generator of the inequality Hrepresentation objects.
EXAMPLES:
sage: triangle = Polyhedron(vertices=[[1,0],[0,1],[1,1]])
sage: for v in triangle.inequality_generator(): print(v)
An inequality (-1, 0) x + 1 >= 0
An inequality (0, -1) x + 1 >= 0
An inequality (1, 1) x + -1 >= 0
sage: [ v for v in triangle.inequality_generator() ]
[An inequality (-1, 0) x + 1 >= 0,
An inequality (0, -1) x + 1 >= 0,
An inequality (1, 1) x + -1 >= 0]
sage: [ [v.A(), v.b()] for v in triangle.inequality_generator() ]
[[(-1, 0), 1], [(0, -1), 1], [(1, 1), -1]]
Returns whether the interior of the polyhedron contains the given point.
EXAMPLES:
sage: P = Polyhedron(vertices=[[0,0],[1,1],[1,-1]])
sage: P.contains( [1,0] )
True
sage: P.interior_contains( [1,0] )
False
If the polyhedron is of strictly smaller dimension than the ambient space, its interior is empty:
sage: P = Polyhedron(vertices=[[0,1],[0,-1]])
sage: P.contains( [0,0] )
True
sage: P.interior_contains( [0,0] )
False
Returns the intersection of one polyhedron with another.
EXAMPLES:
sage: cube = polytopes.n_cube(3)
sage: oct = polytopes.cross_polytope(3)
sage: cube_oct = cube.intersection(oct*2)
sage: len(list( cube_oct.vertex_generator() ))
12
sage: cube_oct
A 3-dimensional polyhedron in QQ^3 defined as the convex hull of 12 vertices.
Tests for boundedness of the polytope.
EXAMPLES:
sage: p = polytopes.icosahedron()
sage: p.is_compact()
True
sage: p = Polyhedron(ieqs = [[0,1,0,0],[0,0,1,0],[0,0,0,1],[1,-1,0,0]])
sage: p.is_compact()
False
Tests for simplicity of a polytope.
EXAMPLES:
sage: p = Polyhedron([[0,0,0],[1,0,0],[0,1,0],[0,0,1]])
sage: p.is_simple()
True
sage: p = Polyhedron([[0,0,0],[4,4,0],[4,0,0],[0,4,0],[2,2,2]])
sage: p.is_simple()
False
REFERENCES:
http://en.wikipedia.org/wiki/Simple_polytope
Returns a generator for the lines of the polyhedron.
EXAMPLES:
sage: pr = Polyhedron(rays = [[1,0],[-1,0],[0,1]], vertices = [[-1,-1]])
sage: pr.line_generator().next().vector()
(1, 0)
Deprecated. Use equations() instead. Returns the linear constraints of the polyhedron. As with inequalities, each constraint is given as [b -a1 -a2 ... an] where for variables x1, x2,..., xn, the polyhedron satisfies the equation b = a1*x1 + a2*x2 + ... + an*xn.
EXAMPLES:
sage: test_p = Polyhedron(vertices = [[1,2,3,4],[2,1,3,4],[4,3,2,1],[3,4,1,2]])
sage: test_p.linearities()
[[-10, 1, 1, 1, 1]]
sage: test_p.linearities() == test_p.equations()
True
Returns a list of lines of the polyhedron. The line data is given as a list of coordinates rather than as a Hrepresentation object.
NOTES:
It is recommended to use line_generator() instead to iterate over the list of Line objects.
EXAMPLES:
sage: p = Polyhedron(rays = [[1,0],[-1,0],[0,1],[1,1]], vertices = [[-2,-2],[2,3]])
sage: p.lines()
[[1, 0]]
sage: p.lines() == [list(x) for x in p.line_generator()]
True
Computes the volume of a polytope.
OUTPUT:
The volume, cast to RDF (although lrs seems to output a rational value this must be an approximation in some cases).
EXAMPLES:
sage: polytopes.n_cube(3).lrs_volume() #optional, needs lrs package installed
8.0
sage: (polytopes.n_cube(3)*2).lrs_volume() #optional, needs lrs package installed
64.0
sage: polytopes.twenty_four_cell().lrs_volume() #optional, needs lrs package installed
2.0
REFERENCES:
David Avis’s lrs program.
Returns the number of objects that make up the H-representation of the polyhedron.
EXAMPLES:
sage: p = polytopes.cross_polytope(4)
sage: p.n_Hrepresentation()
16
sage: p.n_Hrepresentation() == p.n_inequalities() + p.n_equations()
True
Returns the number of objects that make up the V-representation of the polyhedron.
EXAMPLES:
sage: p = polytopes.n_simplex(4)
sage: p.n_Vrepresentation()
5
sage: p.n_Vrepresentation() == p.n_vertices() + p.n_rays() + p.n_lines()
True
Returns the number of equations. The representation will always be minimal, so the number of equations is the codimension of the polyhedron in the ambient space.
EXAMPLES:
sage: p = Polyhedron(vertices = [[1,0,0],[0,1,0],[0,0,1]])
sage: p.n_equations()
1
Returns the number of facets in the polyhedron. This is the same as the n_inequalities function.
EXAMPLES:
sage: p = Polyhedron(vertices = [[t,t^2,t^3] for t in range(6)])
sage: p.n_facets()
8
Returns the number of inequalities. The representation will always be minimal, so the number of inequalities is the number of facets of the polyhedron in the ambient space.
EXAMPLES:
sage: p = Polyhedron(vertices = [[1,0,0],[0,1,0],[0,0,1]])
sage: p.n_inequalities()
3
Returns the number of lines. The representation will always be minimal.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0]], rays=[[0,1],[0,-1]])
sage: p.n_lines()
1
Returns the number of rays. The representation will always be minimal.
EXAMPLES:
sage: p = Polyhedron(vertices = [[1,0],[0,1]], rays=[[1,1]])
sage: p.n_rays()
1
Returns the number of vertices. The representation will always be minimal.
EXAMPLES:
sage: p = Polyhedron(vertices = [[1,0],[0,1],[1,1]], rays=[[1,1]])
sage: p.n_vertices()
2
Returns the polar (dual) polytope. The original vertices are translated so that their barycenter is at the origin, and then the vertices are used as the coefficients in the polar inequalities.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0,1],[0,1,0],[1,0,0],[0,0,0],[1,1,1]])
sage: p
A 3-dimensional polyhedron in QQ^3 defined as the convex hull of 5 vertices.
sage: p.polar()
A 3-dimensional polyhedron in QQ^3 defined as the convex hull of 6 vertices.
Returns a prism of the original polyhedron.
EXAMPLES:
sage: square = polytopes.n_cube(2)
sage: cube = square.prism()
sage: cube
A 3-dimensional polyhedron in QQ^3 defined as the convex hull of 8 vertices.
sage: hypercube = cube.prism()
sage: hypercube.n_vertices()
16
Returns a projection object.
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: proj = p.projection()
sage: proj
The projection of a polyhedron into 3 dimensions.
Returns a polyhedron that is a pyramid over the original.
EXAMPLES:
sage: square = polytopes.n_cube(2)
sage: egyptian_pyramid = square.pyramid()
sage: egyptian_pyramid.n_vertices()
5
sage: for v in egyptian_pyramid.vertex_generator(): print v
A vertex at (0, 1, 1)
A vertex at (0, -1, 1)
A vertex at (0, 1, -1)
A vertex at (0, -1, -1)
A vertex at (1, 0, 0)
Returns the maximal distance from the center to a vertex. All rays and lines are ignored.
NOTES:
The radius for a rational vector is, in general, not rational. use radius_square() if you need a rational distance measure.
EXAMPLES:
sage: p = polytopes.n_cube(4)
sage: p.radius()
8
Returns the square of the maximal distance from the center to a vertex. All rays and lines are ignored.
EXAMPLES:
sage: p = polytopes.permutahedron(4, project = False)
sage: p.radius_square()
720
Returns a generator for the rays of the polyhedron.
EXAMPLES:
sage: pi = Polyhedron(ieqs = [[1,1,0],[1,0,1]])
sage: pir = pi.ray_generator()
sage: [x.vector() for x in pir]
[(1, 0), (0, 1)]
Returns a list of rays as coefficient lists.
NOTES:
It is recommended to use ray_generator() instead to iterate over the list of Ray objects.
OUTPUT:
A list of rays as lists of coordinates.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,0,0,1],[0,0,1,0],[1,1,0,0]])
sage: p.rays()
[[1, 0, 0], [0, 1, 0], [0, 0, 1]]
sage: p.rays() == [list(r) for r in p.ray_generator()]
True
Returns solid rendering of a 2- or 3-d polytope.
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: p_solid = p.render_solid(opacity = .7)
sage: type(p_solid)
<class 'sage.plot.plot3d.base.Graphics3dGroup'>
For polytopes in 2 or 3 dimensions, returns the edges as a list of lines.
EXAMPLES:
sage: p = Polyhedron([[1,2,],[1,1],[0,0]])
sage: p_wireframe = p.render_wireframe()
sage: p_wireframe._Graphics__objects
[Line defined by 2 points, Line defined by 2 points, Line defined by 2 points]
Returns a projection object whose transformed coordinates are a Schlegel projection of the polyhedron.
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: sch_proj = p.schlegel_projection()
sage: schlegel_edge_indices = sch_proj.lines
sage: schlegel_edges = [sch_proj.coordinates_of(x) for x in schlegel_edge_indices]
sage: len([x for x in schlegel_edges if x[0][0] > 0])
8
Returns a simplicial complex from a triangulation of the polytope.
Warning: This first triangulates the polytope using triangulated_facial_incidences, and this function may fail in dimensions greater than 3, although it usually doesn’t.
OUTPUT:
A simplicial complex.
EXAMPLES:
sage: p = polytopes.cuboctahedron()
sage: sc = p.simplicial_complex()
sage: sc
Simplicial complex with 13 vertices and 20 facets
Returns a list of the form [face_index, [v_i_0, v_i_1,...,v_i_{n-1}]] where the face_index refers to the original defining inequality. For a given face, the collection of triangles formed by each list of v_i should triangulate that face.
In dimensions greater than 3, this is computed by randomly lifting each face up a dimension; this does not always work! This should eventually be fixed by using lrs or another program that computes triangulations.
EXAMPLES:
If the figure is already composed of triangles, then all is well:
sage: Polyhedron(vertices = [[5,0,0],[0,5,0],[5,5,0],[2,2,5]]).triangulated_facial_incidences()
[[0, [0, 2, 3]], [1, [0, 1, 2]], [2, [1, 2, 3]], [3, [0, 1, 3]]]
Otherwise some faces get split up to triangles:
p = polytopes.regular_polygon(5)
sage: Polyhedron(vertices = [[2,0,0],[4,1,0],[0,5,0],[5,5,0],[1,1,0],[0,0,1]]).triangulated_facial_incidences()
[[0, [0, 1, 5]], [1, [0, 4, 5]], [2, [2, 4, 5]], [3, [2, 3, 5]], [4, [1, 3, 5]], [5, [0, 1, 4]], [5, [1, 4, 3]], [5, [4, 3, 2]]]
Deprecated. Use 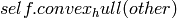 instead.
instead.
EXAMPLES:
sage: Polyhedron(vertices=[[0]]).union( Polyhedron(vertices=[[1]]) )
doctest:...: DeprecationWarning: (Since Sage Version 4.4.4) The function union is replaced by convex_hull.
A 1-dimensional polyhedron in QQ^1 defined as the convex hull of 2 vertices.
Returns a list of vertex indices and their adjacent vertices.
NOTES:
Instead of working with vertex indices, you can use the V-representation objects directly (see examples).
OUTPUT:
The vertex indices are the indices of the V-representation objects.
EXAMPLES:
sage: permuta3 = Polyhedron(vertices = permutations([1,2,3,4]))
sage: permuta3.vertex_adjacencies()[0:3]
[[0, [1, 2, 6]], [1, [0, 3, 7]], [2, [0, 4, 8]]]
sage: v0 = permuta3.Vrepresentation(0)
sage: v0.index() == 0
True
sage: list( v0.neighbors() )
[A vertex at (1, 2, 4, 3), A vertex at (1, 3, 2, 4), A vertex at (2, 1, 3, 4)]
sage: v0_adjacencies = [v0.index(), [v.index() for v in v0.neighbors()]]
sage: permuta3.vertex_adjacencies()[0] == v0_adjacencies
True
Returns the binary matrix of vertex adjacencies.
EXAMPLES:
sage: polytopes.n_simplex(4).vertex_adjacency_matrix()
[0 1 1 1 1]
[1 0 1 1 1]
[1 1 0 1 1]
[1 1 1 0 1]
[1 1 1 1 0]
Returns a generator for the vertices of the polyhedron.
EXAMPLES:
sage: triangle = Polyhedron(vertices=[[1,0],[0,1],[1,1]])
sage: for v in triangle.vertex_generator(): print(v)
A vertex at (1, 0)
A vertex at (0, 1)
A vertex at (1, 1)
sage: v_gen = triangle.vertex_generator()
sage: v_gen.next() # the first vertex
A vertex at (1, 0)
sage: v_gen.next() # the second vertex
A vertex at (0, 1)
sage: v_gen.next() # the third vertex
A vertex at (1, 1)
sage: try: v_gen.next() # there are only three vertices
... except StopIteration: print "STOP"
STOP
sage: type(v_gen)
<type 'generator'>
sage: [ v for v in triangle.vertex_generator() ]
[A vertex at (1, 0), A vertex at (0, 1), A vertex at (1, 1)]
Returns a graph in which the vertices correspond to vertices of the polyhedron, and edges to edges.
EXAMPLES:
sage: g3 = polytopes.n_cube(3).vertex_graph()
sage: len(g3.automorphism_group())
48
sage: s4 = polytopes.n_simplex(4).vertex_graph()
sage: s4.is_eulerian()
True
Returns the vertex-face incidences in the form ![[v_i, [f_{i_0}, f_{i_1},\dots ,f_{i_2}]]](../../_images/math/3590fab0b247f11c2f36d597dde5bd74b87905b9.png) .
.
NOTES:
Instead of working with face/vertex indices, you can use the H-representation/V-representation objects directly (see examples).
EXAMPLES:
sage: from sage.geometry.polyhedra import polytopes
sage: p = polytopes.n_simplex(3)
sage: p.vertex_incidences()
[[0, [0, 1, 3]], [1, [0, 2, 3]], [2, [1, 2, 3]], [3, [0, 1, 2]]]
sage: v0 = p.Vrepresentation(0)
sage: v0.index() == 0
True
sage: p.vertex_incidences()[0] == [ v0.index(), [h.index() for h in v0.incident()] ]
True
Returns a list of vertices of the polyhedron.
NOTES:
It is recommended to use vertex_generator() instead to iterate over the list of Vertex objects.
EXAMPLES:
sage: triangle = Polyhedron(vertices=[[1,0],[0,1],[1,1]])
sage: triangle.vertices()
[[1, 0], [0, 1], [1, 1]]
sage: a_simplex = Polyhedron(ieqs = [[0,1,0,0,0],[0,0,1,0,0],[0,0,0,1,0],[0,0,0,0,1]], eqns = [[1,-1,-1,-1,-1]])
sage: a_simplex.vertices()
[[0, 0, 0, 1], [0, 0, 1, 0], [0, 1, 0, 0], [1, 0, 0, 0]]
sage: a_simplex.vertices() == [list(v) for v in a_simplex.vertex_generator()]
True
Bases: sage.structure.sage_object.SageObject
The internal base class for all representation objects of Polyhedron (vertices/rays/lines and inequalites/equations)
NOTES:
You should not (and cannot) instantiate it yourself. You can only obtain them from a Polyhedron() class.
Returns an arbitrary but fixed number according to the internal storage order.
NOTES:
H-representation and V-representation objects are enumerated independently. That is, amongst all vertices/rays/lines there will be one with index()==0, and amongs all inequalities/equations there will be one with index()==0, unless the polyhedron is empty or spans the whole space.
EXAMPLES:
sage: s = Polyhedron(vertices=[[1],[-1]])
sage: first_vertex = s.vertex_generator().next()
sage: first_vertex.index()
0
sage: first_vertex == s.Vrepresentation(0)
True
Returns the underlying polyhedron.
TESTS:
sage: import sage.geometry.polyhedra as P
sage: pr = P.PolyhedronRepresentation(Polyhedron(vertices = [[1,2,3]]), [1,2,3])
sage: pr.polyhedron()
A 0-dimensional polyhedron in QQ^3 defined as the convex hull of 1 vertex.
Returns the vector representation of the representation object.
NOTES:
- For vertices/lines/rays this is a vector of length ambient_dim(). For inequalities and equations this is a vector of length ambient_dim()+1
EXAMPLES:
sage: s = polytopes.cuboctahedron()
sage: v = s.vertex_generator().next()
sage: v
A vertex at (0, -1/2, -1/2)
sage: v.vector()
(0, -1/2, -1/2)
sage: v()
(0, -1/2, -1/2)
sage: type(v())
<type 'sage.modules.vector_rational_dense.Vector_rational_dense'>
A class of constructors for commonly used, famous, or interesting polytopes.
Returns the Birkhoff polytope with n! vertices. Each vertex is a (flattened) n by n permutation matrix.
INPUT:
- n - a positive integer giving the size of the permutation matrices.
EXAMPLES:
sage: b3 = polytopes.Birkhoff_polytope(3)
sage: b3.n_vertices()
6
Also known as the truncated icosahedron, an Archimedean solid. It has 32 faces and 60 vertices. Rational coordinates are not exact.
EXAMPLES:
sage: bb = polytopes.buckyball()
sage: bb.n_vertices()
60
sage: bb.n_inequalities() # number of facets
32
sage: bb.field()
Rational Field
Returns a cross-polytope in dimension dim_n. These are the generalization of the octahedron.
INPUT:
- dim_n - The dimension of the cross-polytope, a positive integer.
OUTPUT:
A Polyhedron object of the dim_n-dimensional cross-polytope, with exact coordinates.
EXAMPLES:
sage: four_cross = polytopes.cross_polytope(4)
sage: four_cross.is_simple()
False
sage: four_cross.n_vertices()
8
An Archimedean solid with 12 vertices and 14 faces. Dual to the rhombic dodecahedron.
EXAMPLES:
sage: co = polytopes.cuboctahedron()
sage: co.n_vertices()
12
sage: co.n_inequalities()
14
Returns a cyclic polytope in dimension=dim_n and with points_n number of points.
INPUT:
- dim_n - a positive integer, the dimension of the polytope.
- points_n - the number of vertices.
OUTPUT:
A cyclic polytope of dim_n with points_n vertices on the moment curve (t,t^2,...,t^n), as Polyhedron object.
EXAMPLES:
sage: c = polytopes.cyclic_polytope(4,10)
sage: c.n_inequalities()
35
Returns a dodecahedron.
INPUT:
- field - Either QQ (in which case a rational approximation to the golden ratio is used) or RDF.
EXAMPLES:
sage: d12 = polytopes.dodecahedron()
sage: d12.n_inequalities()
12
An Archimedean solid with 48 vertices and 26 faces.
EXAMPLES:
sage: gr = polytopes.great_rhombicuboctahedron()
sage: gr.n_vertices()
48
sage: gr.n_inequalities()
26
The hypersimplex in dimension dim_n with d choose k vertices, projected into (dim_n - 1) dimensions.
INPUT:
- n - the numbers (1,...,n) are permuted
- project - If False the polyhedron is left in dimension n.
OUTPUT:
A Polyhedron object representing the hypersimplex.
EXAMPLES:
sage: h_4_2 = polytopes.hypersimplex(4,2) # combinatorially equivalent to octahedron
sage: h_4_2.n_vertices()
6
sage: h_4_2.n_inequalities()
8
Returns an icosahedron with edge length 1. The vertices are rational, so a rational approximation of the golden ratio is used.
INPUT:
- field - Either QQ or RDF. The icosahedron’s coordinates contain the golden ratio, so there is no exact representation possible.
OUTPUT:
A Polyhedron object of a floating point or rational approximation to the regular 3d icosahedron.
EXAMPLES:
sage: ico = polytopes.icosahedron()
sage: sum(sum( ico.vertex_adjacency_matrix() ))/2
30
Returns a cube in the given dimension
INPUT:
- dim_n - The dimension of the cube, a positive integer.
OUTPUT:
A Polyhedron object of the dim_n-dimensional cube, with exact coordinates.
EXAMPLES:
sage: four_cube = polytopes.n_cube(4)
sage: four_cube.is_simple()
True
Returns a rational approximation to a regular simplex in dimension dim_n.
INPUT:
- dim_n - The dimension of the cross-polytope, a positive
integer.
- project - Optional argument, whether to project
orthogonally. Default is True.
OUTPUT:
A Polyhedron object of the dim_n-dimensional simplex.
EXAMPLES:
sage: s5 = polytopes.n_simplex(5)
sage: s5.dim()
5
A matrix of rational approximations to orthonormal vectors to (1,...,1).
INPUT:
OUTPUT:
A matrix over QQ whose rows are close to an orthonormal basis to the subspace normal to (1,...,1).
EXAMPLES:
sage: from sage.geometry.polyhedra import Polytopes
sage: m = Polytopes.orthonormal_1(5)
sage: m
[ 70711/100000 -7071/10000 0 0 0]
[ 1633/4000 1633/4000 -81649/100000 0 0]
[ 7217/25000 7217/25000 7217/25000 -43301/50000 0]
[ 22361/100000 22361/100000 22361/100000 22361/100000 -44721/50000]
This face-regular, vertex-uniform polytope is dual to the truncated icosahedron. It has 60 faces and 32 vertices.
EXAMPLES:
sage: pd = polytopes.pentakis_dodecahedron()
sage: pd.n_vertices()
32
sage: pd.n_inequalities() # number of facets
60
The standard permutahedron of (1,...,n) projected into n-1 dimensions.
INPUT:
- n - the numbers (1,...,n) are permuted
- project - If False the polyhedron is left in dimension n.
OUTPUT:
A Polyhedron object representing the permutahedron.
EXAMPLES:
sage: perm4 = polytopes.permutahedron(4)
sage: perm4
A 3-dimensional polyhedron in QQ^3 defined as the convex hull of 24 vertices.
sage: polytopes.permutahedron(5).show() # long time
Takes a ndim-dimensional point and projects it onto the plane perpendicular to (1,1,...,1).
INPUT:
- fpoint - a list of ndim numbers
EXAMPLES:
sage: from sage.geometry.polyhedra import Polytopes
sage: Polytopes.project_1([1,1,1,1,2])
[1/100000, 1/100000, 1/50000, -559/625]
Returns a regular polygon with n vertices. Over the rational field the vertices may not be exact.
INPUT:
- n - a positive integer, the number of vertices.
EXAMPLES:
sage: octagon = polytopes.regular_polygon(8)
sage: len(octagon.vertices())
8
This face-regular, vertex-uniform polytope is dual to the cuboctahedron. It has 14 vertices and 12 faces.
EXAMPLES:
sage: rd = polytopes.rhombic_dodecahedron()
sage: rd.n_vertices()
14
sage: rd.n_inequalities()
12
Returns the standard 600-cell polytope.
OUTPUT:
A Polyhedron object of the 4-dimensional 600-cell, a regular polytope. In many ways this is an analogue of the icosahedron. The coordinates of this polytope are rational approximations of the true coordinates of the 600-cell, some of which involve the (irrational) golden ratio.
EXAMPLES:
sage: p600 = polytopes.six_hundred_cell() # not tested - very long time
sage: len(list(p600.bounded_edges())) # not tested - very long time
120
An Archimedean solid with 24 vertices and 26 faces.
EXAMPLES:
sage: sr = polytopes.small_rhombicuboctahedron()
sage: sr.n_vertices()
24
sage: sr.n_inequalities()
26
Returns the standard 24-cell polytope.
OUTPUT:
A Polyhedron object of the 4-dimensional 24-cell, a regular polytope. The coordinates of this polytope are exact.
EXAMPLES:
sage: p24 = polytopes.twenty_four_cell()
sage: v = p24.vertex_generator().next()
sage: for adj in v.neighbors(): print adj
A vertex at (1/2, 1/2, 1/2, -1/2)
A vertex at (1/2, 1/2, -1/2, 1/2)
A vertex at (1/2, -1/2, 1/2, 1/2)
A vertex at (-1/2, 1/2, 1/2, 1/2)
A vertex at (0, 0, 0, 1)
A vertex at (0, 0, 1, 0)
A vertex at (0, 1, 0, 0)
A vertex at (1, 0, 0, 0)
Bases: sage.structure.sage_object.SageObject
Converts a coordinate vector to its internal index.
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: proj = p.projection()
sage: proj.coord_index_of(vector((1,1,1)))
0
Converts list of coordinate vectors to the corresponding list of internal indices.
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: proj = p.projection()
sage: proj.coord_indices_of([vector((1,1,1)),vector((1,-1,1))])
[0, 2]
Given a list of indices, returns the projected coordinates.
EXAMPLES:
sage: p = polytopes.n_simplex(4).projection()
sage: p.coordinates_of([1])
[[0, 0, -43301/50000, 22361/100000]]
Returns the identity projection of the polyhedron.
EXAMPLES:
sage: p = polytopes.icosahedron()
sage: from sage.geometry.polyhedra import Projection
sage: pproj = Projection(p)
sage: ppid = pproj.identity()
sage: ppid.dimension
3
Returns the filled interior (a polygon) of a polyhedron in 2d.
EXAMPLES:
sage: cps = [i^3 for i in srange(-2,2,1/5)]
sage: p = Polyhedron(vertices = [[(t^2-1)/(t^2+1),2*t/(t^2+1)] for t in cps])
sage: proj = p.projection()
sage: filled_poly = proj.render_fill_2d()
sage: filled_poly.axes_width()
0.8000...
Returns the outline (edges) of a polyhedron in 2d.
EXAMPLES:
sage: penta = polytopes.regular_polygon(5)
sage: outline = penta.projection().render_outline_2d()
sage: outline._Graphics__objects[0]
Line defined by 2 points
Returns the points of a polyhedron in 2d.
EXAMPLES:
sage: hex = polytopes.regular_polygon(6)
sage: proj = hex.projection()
sage: hex_points = proj.render_points_2d()
sage: hex_points._Graphics__objects
[Point set defined by 6 point(s)]
Returns solid 3d rendering of a 3d polytope.
EXAMPLES:
sage: p = polytopes.n_cube(3).projection()
sage: p_solid = p.render_solid_3d(opacity = .7)
sage: type(p_solid)
<class 'sage.plot.plot3d.base.Graphics3dGroup'>
Returns the 3d rendering of the vertices.
EXAMPLES:
sage: p = polytopes.cross_polytope(3)
sage: proj = p.projection()
sage: verts = proj.render_vertices_3d()
sage: verts.bounding_box()
((-1.0, -1.0, -1.0), (1.0, 1.0, 1.0))
Returns the 3d wireframe rendering.
EXAMPLES:
sage: cube = polytopes.n_cube(3)
sage: cube_proj = cube.projection()
sage: wire = cube_proj.render_wireframe_3d()
sage: print wire.tachyon().split('\n')[77] # for testing
FCylinder base 1.0 -1.0 1.0 apex 1.0 1.0 1.0 rad 0.005 texture...
The Schlegel projection.
The vertices are normalized to the unit sphere, and stereographically projected from a point slightly outside of the sphere.
INPUT:
- projection_direction - The direction of the Schlegel projection. By default, the vector consisting of the first n primes is chosen.
EXAMPLES:
sage: cube4 = polytopes.n_cube(4)
sage: from sage.geometry.polyhedra import Projection
sage: Projection(cube4).schlegel([1,0,0,0])
The projection of a polyhedron into 3 dimensions.
sage: _.show()
The stereographic projection.
INPUT:
EXAMPLES:
sage: from sage.geometry.polyhedra import Projection
sage: proj = Projection(polytopes.buckyball()) #long time
sage: proj #long time
The projection of a polyhedron into 3 dimensions.
sage: proj.stereographic([5,2,3]).show() #long time
sage: Projection( polytopes.twenty_four_cell() ).stereographic([2,0,0,0])
The projection of a polyhedron into 3 dimensions.
The Schlegel projection from the given input point.
EXAMPLES:
sage: from sage.geometry.polyhedra import ProjectionFuncSchlegel
sage: proj = ProjectionFuncSchlegel([2,2,2])
sage: proj(vector([1.1,1.1,1.11]))[0]
0.0302...
The stereographic (or perspective) projection.
EXAMPLES:
sage: from sage.geometry.polyhedra import ProjectionFuncStereographic
sage: cube = polytopes.n_cube(3).vertices()
sage: proj = ProjectionFuncStereographic([1.1,1.1,1.1])
sage: ppoints = [proj(vector(x)) for x in cube]
sage: ppoints[0]
(0.0, 0.0)
Bases: sage.geometry.polyhedra.Vrepresentation
A ray of the polyhedron. Inherits from Vrepresentation.
Returns 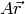
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,0,1],[0,1,0],[1,-1,0]])
sage: a = p.ray_generator().next()
sage: h = p.inequality_generator().next()
sage: a.evaluated_on(h)
1
Tests if this object is a ray. Always True by construction.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,0,1],[0,1,0],[1,-1,0]])
sage: a = p.ray_generator().next()
sage: a.is_ray()
True
Bases: sage.geometry.polyhedra.Vrepresentation
A vertex of the polyhedron. Inherits from Vrepresentation.
Returns 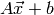
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: v = p.vertex_generator().next()
sage: h = p.inequality_generator().next()
sage: v
A vertex at (1, 1, 1)
sage: h
An inequality (0, 0, 1) x + 1 >= 0
sage: v.evaluated_on(h)
2
Tests if this object is a vertex. By construction it always is.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[0,0,1],[0,1,0],[1,-1,0]])
sage: a = p.vertex_generator().next()
sage: a.is_vertex()
True
Bases: sage.geometry.polyhedra.PolyhedronRepresentation
The base class for V-representation objects of a polyhedron. Inherits from PolyhedronRepresentation.
Alias for neighbors().
TESTS:
sage: p = Polyhedron(vertices = [[0,0],[1,0],[0,3],[1,4]])
sage: v = p.vertex_generator().next()
sage: a = v.neighbors().next()
sage: b = v.adjacent().next()
sage: a==b
True
Returns a generator for the equations/inequalities that are satisfied on the given vertex/ray/line.
EXAMPLES:
sage: triangle = Polyhedron(vertices=[[1,0],[0,1],[-1,-1]])
sage: ineq = triangle.inequality_generator().next()
sage: ineq
An inequality (-1, -1) x + 1 >= 0
sage: [ v for v in ineq.incident()]
[A vertex at (1, 0), A vertex at (0, 1)]
sage: p = Polyhedron(vertices=[[0,0,0],[0,1,0],[0,0,1]], rays=[[1,-1,-1]])
sage: ineq = p.Hrepresentation(2)
sage: ineq
An inequality (1, 1, 0) x + 0 >= 0
sage: [ x for x in ineq.incident() ]
[A ray in the direction (1, -1, -1),
A vertex at (0, 0, 0),
A vertex at (0, 0, 1)]
Returns True if the object is part of a V-representation (a vertex, ray, or line).
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0],[1,0],[0,3],[1,3]])
sage: v = p.vertex_generator().next()
sage: v.is_V()
True
Returns whether the incidence matrix element (self,Hobj) == 1
EXAMPLES:
sage: p = polytopes.n_cube(3)
sage: h1 = p.inequality_generator().next()
sage: h1
An inequality (0, 0, 1) x + 1 >= 0
sage: v1 = p.vertex_generator().next()
sage: v1
A vertex at (1, 1, 1)
sage: v1.is_incident(h1)
False
Returns True if the object is a line of the V-representation. This method is over-ridden by the corresponding method in the derived class Line.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[1, 0, 0, 0, 1], [1, 1, 0, 0, 0], [1, 0, 1, 0, 0]])
sage: line1 = p.line_generator().next()
sage: line1.is_line()
True
sage: v1 = p.vertex_generator().next()
sage: v1.is_line()
False
Returns True if the object is a ray of the V-representation. This method is over-ridden by the corresponding method in the derived class Ray.
EXAMPLES:
sage: p = Polyhedron(ieqs = [[1, 0, 0, 0, 1], [1, 1, 0, 0, 0], [1, 0, 1, 0, 0]])
sage: r1 = p.ray_generator().next()
sage: r1.is_ray()
True
sage: v1 = p.vertex_generator().next()
sage: v1
A vertex at (-1, -1, 0, -1)
sage: v1.is_ray()
False
Returns True if the object is a vertex of the V-representation. This method is over-ridden by the corresponding method in the derived class Vertex.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0],[1,0],[0,3],[1,3]])
sage: v = p.vertex_generator().next()
sage: v.is_vertex()
True
sage: p = Polyhedron(ieqs = [[1, 0, 0, 0, 1], [1, 1, 0, 0, 0], [1, 0, 1, 0, 0]])
sage: r1 = p.ray_generator().next()
sage: r1.is_vertex()
False
Returns a generator for the adjacent vertices/rays/lines.
EXAMPLES:
sage: p = Polyhedron(vertices = [[0,0],[1,0],[0,3],[1,4]])
sage: v = p.vertex_generator().next()
sage: v.neighbors().next()
A vertex at (1, 0)
Return a string containing the H-representation in cddlib’s ine format.
EXAMPLES:
sage: from sage.geometry.polyhedra import cdd_Hrepresentation
sage: cdd_Hrepresentation('rational', None, [[0,1]])
'H-representation\nlinearity 1 1\nbegin\n 1 2 rational\n 0 1\nend\n'
Return a string containing the V-representation in cddlib’s ext format.
NOTE:
If there is no vertex given, then the origin will be implicitly added. You cannot write the empty V-representation (which cdd would refuse to process).
EXAMPLES:
sage: from sage.geometry.polyhedra import cdd_Vrepresentation
sage: print cdd_Vrepresentation('rational', [[0,0]], [[1,0]], [[0,1]])
V-representation
linearity 1 1
begin
3 3 rational
0 0 1
0 1 0
1 0 0
end
Returns the vertices/rays in cyclic order if possible.
NOTES:
This works if and only if each vertex/ray is adjacent to exactly two others. For example, any 2-dimensional polyhedron satisfies this.
EXAMPLES:
sage: from sage.geometry.polyhedra import cyclic_sort_vertices_2d
sage: square = Polyhedron([[1,0],[-1,0],[0,1],[0,-1]])
sage: vertices = [v for v in square.vertex_generator()]
sage: vertices
[A vertex at (1, 0),
A vertex at (-1, 0),
A vertex at (0, 1),
A vertex at (0, -1)]
sage: cyclic_sort_vertices_2d(vertices)
[A vertex at (0, -1),
A vertex at (1, 0),
A vertex at (0, 1),
A vertex at (-1, 0)]
The identity projection.
EXAMPLES:
sage: from sage.geometry.polyhedra import projection_func_identity
sage: projection_func_identity((1,2,3))
[1, 2, 3]
Returns 2d rendering of the projection of a polyhedron into 2-dimensional ambient space.
EXAMPLES:
sage: p1 = Polyhedron(vertices=[[1,1]], rays=[[1,1]])
sage: q1 = p1.projection()
sage: p2 = Polyhedron(vertices=[[1,0], [0,1], [0,0]])
sage: q2 = p2.projection()
sage: p3 = Polyhedron(vertices=[[1,2]])
sage: q3 = p3.projection()
sage: p4 = Polyhedron(vertices=[[2,0]], rays=[[1,-1]], lines=[[1,1]])
sage: q4 = p4.projection()
sage: q1.show() + q2.show() + q3.show() + q4.show()
sage: from sage.geometry.polyhedra import render_2d
sage: q = render_2d(p1.projection())
sage: q._Graphics__objects
[Point set defined by 1 point(s), Arrow from (1.0,1.0) to (2.0,2.0), Polygon defined by 3 points]
Returns 3d rendering of a polyhedron projected into 3-dimensional ambient space.
NOTE:
This method, render_3d, is used in the show() method of a polyhedron if it is in 3 dimensions.
EXAMPLES:
sage: p1 = Polyhedron(vertices=[[1,1,1]], rays=[[1,1,1]])
sage: p2 = Polyhedron(vertices=[[2,0,0], [0,2,0], [0,0,2]])
sage: p3 = Polyhedron(vertices=[[1,0,0], [0,1,0], [0,0,1]], rays=[[-1,-1,-1]])
sage: p1.projection().show() + p2.projection().show() + p3.projection().show()
It correctly handles various degenerate cases:
sage: Polyhedron(lines=[[1,0,0],[0,1,0],[0,0,1]]).show() # whole space
sage: Polyhedron(vertices=[[1,1,1]], rays=[[1,0,0]], lines=[[0,1,0],[0,0,1]]).show() # half space
sage: Polyhedron(vertices=[[1,1,1]], lines=[[0,1,0],[0,0,1]]).show() # R^2 in R^3
sage: Polyhedron(rays=[[0,1,0],[0,0,1]], lines=[[1,0,0]]).show() # quadrant wedge in R^2
sage: Polyhedron(rays=[[0,1,0]], lines=[[1,0,0]]).show() # upper half plane in R^3
sage: Polyhedron(lines=[[1,0,0]]).show() # R^1 in R^2
sage: Polyhedron(rays=[[0,1,0]]).show() # Half-line in R^3
sage: Polyhedron(vertices=[[1,1,1]]).show() # point in R^3
Returns a 3d rendering of the Schlegel projection of a 4d polyhedron projected into 3-dimensional space.
NOTES:
The show() method of Polyhedron() uses this to draw itself if the ambient dimension is 4.
INPUT:
EXAMPLES:
sage: poly = polytopes.twenty_four_cell()
sage: poly
A 4-dimensional polyhedron in QQ^4 defined as the convex hull of 24 vertices.
sage: poly.show()
sage: poly.show(projection_direction=[2,5,11,17])
sage: type( poly.show() )
<class 'sage.plot.plot3d.base.Graphics3dGroup'>
TESTS:
sage: from sage.geometry.polyhedra import render_4d
sage: p = polytopes.n_cube(4)
sage: q = render_4d(p)
sage: tach_str = q.tachyon()
sage: tach_str.count('FCylinder')
32