Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
A right (respectively left) Yamanouchi word on a completely ordered alphabet, for instance [1,2,...,n], is a word math such that any right (respectively left) factor of math contains more entries math than math. For example, the word [2, 3, 2, 2, 1, 3, 1, 2, 1, 1] is a right Yamanouchi one.
The evaluation of a word math encodes the number of occurrences of each letter of math. In the case of Yamanouchi words, the evaluation is a partition. For example, the word [2, 3, 2, 2, 1, 3, 1, 2, 1, 1] has evaluation [4, 4, 2].
Yamanouchi words can be useful in the computation of
Littlewood-Richardson coefficients  .
According to the Littlewood-Richardson
rule,
.
According to the Littlewood-Richardson
rule,  is the number of skew tableaux
of shape
is the number of skew tableaux
of shape  and evaluation
and evaluation 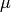 ,
whose row readings are Yamanouchi words.
,
whose row readings are Yamanouchi words.