Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Words »

AUTHORS:
- Franco Saliola (2008-12-17): merged into sage
- Sebastien Labbe (2008-12-17): merged into sage
- Arnaud Bergeron (2008-12-17): merged into sage
- Amy Glen (2008-12-17): merged into sage
- Sebastien Labbe (2009-12-19): Added S-adic words (ticket #7543)
USE:
To see a list of all word constructors, type “words.” and then press the tab key. The documentation for each constructor includes information about each word, which provides a useful reference.
EXAMPLES:
sage: t = words.ThueMorseWord(); t
word: 0110100110010110100101100110100110010110...
Bases: sage.combinat.words.word.FiniteWord_list
Returns the lower Christoffel word of slope 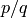 , where
, where  and
and
 are relatively prime non-negative integers, over the given
two-letter alphabet.
are relatively prime non-negative integers, over the given
two-letter alphabet.
The Christoffel word of slope `p/q` is obtained from the
Cayley graph of 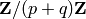 with generator
with generator  as
follows. If
as
follows. If  is an edge in the Cayley graph, then
is an edge in the Cayley graph, then
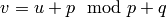 . Label the edge
. Label the edge  by
alphabet[1] if
by
alphabet[1] if 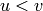 and alphabet[0] otherwise. The Christoffel
word is the word obtained by reading the edge labels along the
cycle beginning from 0.
and alphabet[0] otherwise. The Christoffel
word is the word obtained by reading the edge labels along the
cycle beginning from 0.
EXAMPLES:
sage: words.LowerChristoffelWord(4,7)
word: 00100100101
sage: words.LowerChristoffelWord(4,7,alphabet='ab')
word: aabaabaabab
TESTS:
sage: words.LowerChristoffelWord(1,0)
word: 1
sage: words.LowerChristoffelWord(0,1,'xy')
word: x
sage: words.LowerChristoffelWord(1,1)
word: 01
Returns the Markoff number associated to the Christoffel word self.
The Markoff number of a Christoffel word  is
is 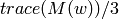 ,
where
,
where 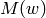 is the
is the 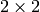 matrix obtained by applying the
morphism:
0 -> matrix(2,[2,1,1,1])
1 -> matrix(2,[5,2,2,1])
matrix obtained by applying the
morphism:
0 -> matrix(2,[2,1,1,1])
1 -> matrix(2,[5,2,2,1])
EXAMPLES:
sage: w0 = words.LowerChristoffelWord(4,7)
sage: w1, w2 = w0.standard_factorization()
sage: (m0,m1,m2) = (w.markoff_number() for w in (w0,w1,w2))
sage: (m0,m1,m2)
(294685, 13, 7561)
sage: m0**2 + m1**2 + m2**2 == 3*m0*m1*m2
True
Returns the standard factorization of the Christoffel word self.
The standard factorization of a Christoffel word  is the
unique factorization of
is the
unique factorization of  into two Christoffel words.
into two Christoffel words.
EXAMPLES:
sage: w = words.LowerChristoffelWord(5,9)
sage: print w
word: 00100100100101
sage: w1, w2 = w.standard_factorization()
sage: print w1
word: 001
sage: print w2
word: 00100100101
sage: w = words.LowerChristoffelWord(51,37)
sage: w1, w2 = w.standard_factorization()
sage: w1
word: 0101011010101101011
sage: w2
word: 0101011010101101011010101101010110101101...
sage: w1 * w2 == w
True
Bases: object
Constructor of several famous words.
EXAMPLES:
sage: words.ThueMorseWord()
word: 0110100110010110100101100110100110010110...
sage: words.FibonacciWord()
word: 0100101001001010010100100101001001010010...
sage: words.ChristoffelWord(5, 8)
word: 0010010100101
sage: words.RandomWord(10, 4) # not tested random
word: 1311131221
sage: words.CodingOfRotationWord(alpha=0.618, beta=0.618)
word: 1010110101101101011010110110101101101011...
sage: tm = WordMorphism('a->ab,b->ba')
sage: fib = WordMorphism('a->ab,b->a')
sage: tmword = words.ThueMorseWord([0, 1])
sage: from itertools import repeat
sage: words.s_adic(tmword, repeat('a'), {0:tm, 1:fib})
word: abbaababbaabbaabbaababbaababbaabbaababba...
Note
To see a list of all word constructors, type words. and then hit the TAB key. The documentation for each constructor includes information about each word, which provides a useful reference.
TESTS:
sage: from sage.combinat.words.word_generators import WordGenerator
sage: words2 = WordGenerator()
sage: type(loads(dumps(words2)))
<class 'sage.combinat.words.word_generators.WordGenerator'>
Returns the characteristic Sturmian word (also called standard Sturmian word) of given slope.
Over a binary alphabet 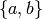 , the characteristic Sturmian
word
, the characteristic Sturmian
word 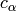 of irrational slope
of irrational slope  is the infinite word
satisfying
is the infinite word
satisfying 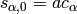 and
and 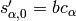 ,
where
,
where 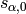 and
and 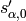 are respectively the lower
and upper mechanical words with slope
are respectively the lower
and upper mechanical words with slope  and intercept
and intercept  .
Equivalently, for irrationnal
.
Equivalently, for irrationnal  ,
,
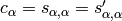 .
.
Let ![\alpha = [0, d_1 + 1, d_2, d_3, \ldots]](../../../_images/math/28f854f3df220e8b053aeb87de2ca199d9314697.png) be the continued
fraction expansion of
be the continued
fraction expansion of  . It has been shown that the
characteristic Sturmian word of slope
. It has been shown that the
characteristic Sturmian word of slope  is also the limit of
the sequence:
is also the limit of
the sequence: 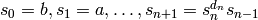 for
for 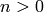 .
.
See Section 2.1 of [1] for more details.
INPUT:
![]0, 1[](../../../_images/math/011c4b0c26fa7e791477a453d7bd05b2d4cfaa9e.png)
![]0, 1[](../../../_images/math/011c4b0c26fa7e791477a453d7bd05b2d4cfaa9e.png)
OUTPUT:
word
ALGORITHM:
Let ![[0, d_1 + 1, d_2, d_3, \ldots]](../../../_images/math/e7708d96a9ace9d353e82a1a6ec136ae8bf37d98.png) be the continued fraction
expansion of
be the continued fraction
expansion of  . Then, the characteristic Sturmian word of
slope
. Then, the characteristic Sturmian word of
slope  is the limit of the sequence:
is the limit of the sequence: 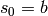 ,
, 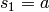 and
and 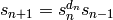 for
for 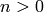 .
.
EXAMPLES:
From real slope:
sage: words.CharacteristicSturmianWord(1/golden_ratio^2)
word: 0100101001001010010100100101001001010010...
sage: words.CharacteristicSturmianWord(4/5)
word: 11110
sage: words.CharacteristicSturmianWord(5/14)
word: 01001001001001
sage: words.CharacteristicSturmianWord(pi-3)
word: 0000001000000100000010000001000000100000...
From an iterator of the continued fraction expansion of a real:
sage: def cf():
... yield 0
... yield 2
... while True: yield 1
sage: F = words.CharacteristicSturmianWord(cf()); F
word: 0100101001001010010100100101001001010010...
sage: Fib = words.FibonacciWord(); Fib
word: 0100101001001010010100100101001001010010...
sage: F[:10000] == Fib[:10000]
True
The alphabet may be specified:
sage: words.CharacteristicSturmianWord(cf(), 'rs')
word: rsrrsrsrrsrrsrsrrsrsrrsrrsrsrrsrrsrsrrsr...
The characteristic sturmian word of slope 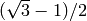 :
:
sage: words.CharacteristicSturmianWord((sqrt(3)-1)/2)
word: 0100100101001001001010010010010100100101...
The same word defined from the continued fraction expansion of
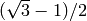 :
:
sage: from itertools import cycle, chain
sage: it = chain([0], cycle([2, 1]))
sage: words.CharacteristicSturmianWord(it)
word: 0100100101001001001010010010010100100101...
The first terms of the standard sequence of the characteristic
sturmian word of slope 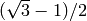 :
:
sage: words.CharacteristicSturmianWord([0,2])
word: 01
sage: words.CharacteristicSturmianWord([0,2,1])
word: 010
sage: words.CharacteristicSturmianWord([0,2,1,2])
word: 01001001
sage: words.CharacteristicSturmianWord([0,2,1,2,1])
word: 01001001010
sage: words.CharacteristicSturmianWord([0,2,1,2,1,2])
word: 010010010100100100101001001001
sage: words.CharacteristicSturmianWord([0,2,1,2,1,2,1])
word: 0100100101001001001010010010010100100101...
TESTS:
sage: words.CharacteristicSturmianWord([1,1,1],'xyz')
...
TypeError: alphabet does not contain two distinct elements
sage: words.CharacteristicSturmianWord(5/4)
...
ValueError: The argument slope (=5/4) must be in ]0,1[.
sage: words.CharacteristicSturmianWord(1/golden_ratio^2, bits=30)
word: 0100101001001010010100100101001001010010...
sage: _.length()
28657
sage: a = words.LowerMechanicalWord(1/pi)[1:]
sage: b = words.UpperMechanicalWord(1/pi)[1:]
sage: c = words.CharacteristicSturmianWord(1/pi)
sage: n = 500; a[:n] == b[:n] == c[:n]
True
sage: alpha = random()
sage: c = words.CharacteristicSturmianWord(alpha)
sage: l = words.LowerMechanicalWord(alpha)[1:]
sage: u = words.UpperMechanicalWord(alpha)[1:]
sage: i = 10000; j = i + 500; c[i:j] == l[i:j] == u[i:j]
True
sage: a, b = 207, 232
sage: u = words.ChristoffelWord(a, b)
sage: v = words.CharacteristicSturmianWord(a/(a+b))
sage: u[1:-1] == v[:-2]
True
REFERENCES:
Returns the infinite word obtained from the coding of rotation of
parameters 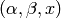 over the given two-letter alphabet.
over the given two-letter alphabet.
The coding of rotation corresponding to the parameters
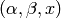 is the symbolic sequence
is the symbolic sequence 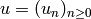 defined over the binary alphabet
defined over the binary alphabet 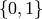 by
by 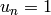 if
if
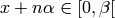 and
and 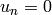 otherwise. See [1].
otherwise. See [1].
EXAMPLES:
sage: alpha = 0.45
sage: beta = 0.48
sage: words.CodingOfRotationWord(0.45, 0.48)
word: 1101010101001010101011010101010010101010...
sage: words.CodingOfRotationWord(0.45, 0.48, alphabet='xy')
word: yyxyxyxyxyxxyxyxyxyxyyxyxyxyxyxxyxyxyxyx...
TESTS:
sage: words.CodingOfRotationWord(0.51,0.43,alphabet=[1,0,2])
...
TypeError: alphabet does not contain two distinct elements
REFERENCES:
Returns the Fibonacci word on the given two-letter alphabet.
INPUT:
Recursive construction: the Fibonacci word is the limit of the
following sequence of words: 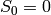 ,
, 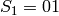 ,
,
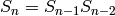 for
for 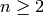 .
.
Fixed point construction: the Fibonacci word is the fixed point of the
morphism: 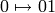 and
and 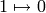 . Hence, it can be constructed
by the following read-write process:
. Hence, it can be constructed
by the following read-write process:
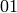 ,
,  , append
, append 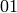 to the word;
to the word; , append
, append  to the word;
to the word;Function: Over the alphabet 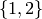 , the n-th letter of the
Fibonacci word is
, the n-th letter of the
Fibonacci word is
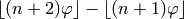 where
where 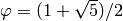 is the golden ratio.
is the golden ratio.
EXAMPLES:
sage: w = words.FibonacciWord(construction_method="recursive"); w
word: 0100101001001010010100100101001001010010...
sage: v = words.FibonacciWord(construction_method="recursive", alphabet='ab'); v
word: abaababaabaababaababaabaababaabaababaaba...
sage: u = words.FibonacciWord(construction_method="fixed point"); u
word: 0100101001001010010100100101001001010010...
sage: words.FibonacciWord(construction_method="fixed point", alphabet=[4, 1])
word: 4144141441441414414144144141441441414414...
sage: words.FibonacciWord([0,1], 'function')
word: 0100101001001010010100100101001001010010...
sage: words.FibonacciWord('ab', 'function')
word: abaababaabaababaababaabaababaabaababaaba...
TESTS:
sage: from math import floor, sqrt
sage: golden_ratio = (1 + sqrt(5))/2.0
sage: a = golden_ratio / (1 + 2*golden_ratio)
sage: wn = lambda n : int(floor(a*(n+2)) - floor(a*(n+1)))
sage: f = Words([0,1])(wn); f
word: 0100101001001010010100100101001001010010...
sage: f[:10000] == w[:10000]
True
sage: f[:10000] == u[:10000] #long time
True
sage: words.FibonacciWord("abc")
...
TypeError: alphabet does not contain two distinct elements
Returns the fixed point of the morphism beginning with first_letter.
A fixed point of a morphism 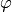 is a word
is a word  such that
such that
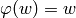 .
.
INPUT:
EXAMPLES:
sage: mu = {0:[0,1], 1:[1,0]}
sage: tm = words.FixedPointOfMorphism(mu,0); tm
word: 0110100110010110100101100110100110010110...
sage: TM = words.ThueMorseWord()
sage: tm[:1000] == TM[:1000]
True
sage: mu = {0:[0,1], 1:[0]}
sage: f = words.FixedPointOfMorphism(mu,0); f
word: 0100101001001010010100100101001001010010...
sage: F = words.FibonacciWord(); F
word: 0100101001001010010100100101001001010010...
sage: f[:1000] == F[:1000]
True
sage: fp = words.FixedPointOfMorphism('a->abc,b->,c->','a'); fp
word: abc
Returns the lower mechanical word with slope  and
intercept
and
intercept 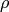
The lower mechanical word 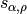 with
slope
with
slope  and intercept
and intercept 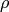 is defined by
is defined by
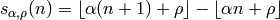 [1].
[1].
INPUT:
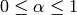
OUTPUT:
infinite word
EXAMPLES:
sage: words.LowerMechanicalWord(1/golden_ratio^2)
word: 0010010100100101001010010010100100101001...
sage: words.LowerMechanicalWord(1/5)
word: 0000100001000010000100001000010000100001...
sage: words.LowerMechanicalWord(1/pi)
word: 0001001001001001001001000100100100100100...
TESTS:
sage: m = words.LowerMechanicalWord(1/golden_ratio^2)[1:]
sage: s = words.CharacteristicSturmianWord(1/golden_ratio^2)
sage: m[:500] == s[:500]
True
REFERENCES:
This function finds and returns the minimal smooth prefix of length n.
See [1] for a definition.
INPUT:
OUTPUT:
word – the prefix
NOTE:
Be patient, this function can take a really long time if asked for a large prefix.
EXAMPLES:
sage: words.MinimalSmoothPrefix(10)
word: 1212212112
REFERENCES:
Returns a random word of length  over the given
over the given  -letter
alphabet.
-letter
alphabet.
INPUT:
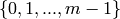 ) any container of
length m that is suitable to build an instance of
OrderedAlphabet (list, tuple, str, ...)
) any container of
length m that is suitable to build an instance of
OrderedAlphabet (list, tuple, str, ...)EXAMPLES:
sage: words.RandomWord(10) # random results
word: 0110100101
sage: words.RandomWord(10, 4) # random results
word: 0322313320
sage: words.RandomWord(100, 7) # random results
word: 2630644023642516442650025611300034413310...
sage: words.RandomWord(100, 7, range(-3,4)) # random results
word: 1,3,-1,-1,3,2,2,0,1,-2,1,-1,-3,-2,2,0,3,0,-3,0,3,0,-2,-2,2,0,1,-3,2,-2,-2,2,0,2,1,-2,-3,-2,-1,0,...
sage: words.RandomWord(100, 5, "abcde") # random results
word: acebeaaccdbedbbbdeadeebbdeeebeaaacbadaac...
sage: words.RandomWord(17, 5, "abcde") # random results
word: dcacbbecbddebaadd
TESTS:
sage: words.RandomWord(2,3,"abcd")
...
TypeError: alphabet does not contain 3 distinct elements
Returns the standard episturmian word (or epistandard word) directed by directive_word. Over a 2-letter alphabet, this function gives characteristic Sturmian words.
An infinite word  over a finite alphabet
over a finite alphabet  is said to be
standard episturmian (or epistandard) iff there exists an
infinite word
is said to be
standard episturmian (or epistandard) iff there exists an
infinite word 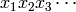 over
over  (called the directive
word of
(called the directive
word of  ) such that
) such that  is the limit as
is the limit as  goes to infinity of
goes to infinity of
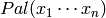 , where
, where 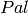 is the iterated palindromic closure
function.
is the iterated palindromic closure
function.
Note that an infinite word is episturmian if it has the same set of factors as some epistandard word.
See for instance [1], [2], and [3].
INPUT:
EXAMPLES:
sage: Fibonacci = words.StandardEpisturmianWord(Words('ab')('ab')); Fibonacci
word: abaababaabaababaababaabaababaabaababaaba...
sage: Tribonacci = words.StandardEpisturmianWord(Words('abc')('abc')); Tribonacci
word: abacabaabacababacabaabacabacabaabacababa...
sage: S = words.StandardEpisturmianWord(Words('abcd')('aabcabada')); S
word: aabaacaabaaabaacaabaabaacaabaaabaacaabaa...
sage: S = words.StandardEpisturmianWord(Fibonacci); S
word: abaabaababaabaabaababaabaababaabaabaabab...
sage: S[:25]
word: abaabaababaabaabaababaaba
sage: S = words.StandardEpisturmianWord(Tribonacci); S
word: abaabacabaabaabacabaababaabacabaabaabaca...
sage: words.StandardEpisturmianWord(123)
...
TypeError: directive_word is not a word, so it cannot be used to build an episturmian word
sage: words.StandardEpisturmianWord(Words('ab'))
...
TypeError: directive_word is not a word, so it cannot be used to build an episturmian word
REFERENCES:
Returns the (Generalized) Thue-Morse word over the given alphabet.
There are several ways to define the Thue-Morse word  .
We use the following definition:
.
We use the following definition: ![t[n]](../../../_images/math/2113acbf85681e75fd265fb1a833ff234c7d3c67.png) is the sum modulo
is the sum modulo  of
the digits in the given base expansion of
of
the digits in the given base expansion of  .
.
INPUT:
EXAMPLES:
Thue-Morse word:
sage: t = words.ThueMorseWord(); t
word: 0110100110010110100101100110100110010110...
Thue-Morse word on other alphabets:
sage: t = words.ThueMorseWord('ab'); t
word: abbabaabbaababbabaababbaabbabaabbaababba...
sage: t = words.ThueMorseWord(['L1', 'L2'])
sage: t[:8]
word: L1,L2,L2,L1,L2,L1,L1,L2
Generalized Thue Morse word:
sage: words.ThueMorseWord(alphabet=(0,1,2), base=2)
word: 0112122012202001122020012001011212202001...
sage: t = words.ThueMorseWord(alphabet=(0,1,2), base=5); t
word: 0120112012201200120112012120122012001201...
sage: t[100:130].critical_exponent()
10/3
TESTS:
sage: words.ThueMorseWord(alphabet='ab', base=1)
...
ValueError: base (=1) and len(alphabet) (=2) must be at least 2
REFERENCES:
Returns the upper Christoffel word of slope 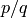 , where
, where
 and
and  are relatively prime non-negative
integers, over the given alphabet.
are relatively prime non-negative
integers, over the given alphabet.
The upper Christoffel word of slope `p/q` is equal to the
reversal of the lower Christoffel word of slope 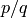 .
Equivalently, if
.
Equivalently, if 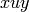 is the lower Christoffel word of
slope
is the lower Christoffel word of
slope 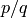 , where
, where  and
and  are letters,
then
are letters,
then 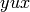 is the upper Christoffel word of slope
is the upper Christoffel word of slope
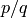 (because
(because  is a palindrome).
is a palindrome).
INPUT:
EXAMPLES:
sage: words.UpperChristoffelWord(1,0)
word: 1
sage: words.UpperChristoffelWord(0,1)
word: 0
sage: words.UpperChristoffelWord(1,1)
word: 10
sage: words.UpperChristoffelWord(4,7)
word: 10100100100
TESTS::
sage: words.UpperChristoffelWord(51,43,"abc")
...
ValueError: alphabet must contain exactly two distinct elements
Returns the upper mechanical word with slope  and
intercept
and
intercept 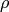
The upper mechanical word 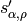 with
slope
with
slope  and intercept
and intercept 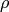 is defined by
is defined by
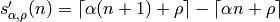 . [1]
. [1]
INPUT:
OUTPUT:
infinite word
EXAMPLES:
sage: words.UpperMechanicalWord(1/golden_ratio^2)
word: 1010010100100101001010010010100100101001...
sage: words.UpperMechanicalWord(1/5)
word: 1000010000100001000010000100001000010000...
sage: words.UpperMechanicalWord(1/pi)
word: 1001001001001001001001000100100100100100...
TESTS:
sage: m = words.UpperMechanicalWord(1/golden_ratio^2)[1:]
sage: s = words.CharacteristicSturmianWord(1/golden_ratio^2)
sage: m[:500] == s[:500]
True
REFERENCES:
Returns the n-th dual Fibonacci Tile [1].
EXAMPLES:
sage: for i in range(4): words.dual_fibonacci_tile(i)
Path: 3210
Path: 32123032301030121012
Path: 3212303230103230321232101232123032123210...
Path: 3212303230103230321232101232123032123210...
REFERENCES:
Returns the n-th Fibonacci Tile [1].
EXAMPLES:
sage: for i in range(3): words.fibonacci_tile(i)
Path: 3210
Path: 323030101212
Path: 3230301030323212323032321210121232121010...
REFERENCES:
Returns the s-adic infinite word obtained from a sequence of morphisms applied on a letter.
DEFINITION (from [1]):
Let  be a infinite word over an alphabet
be a infinite word over an alphabet 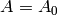 . A
standard representation of
. A
standard representation of  is obtained from a sequence of
substitutions
is obtained from a sequence of
substitutions 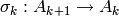 and a sequence of letters
and a sequence of letters
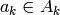 such that:
such that:
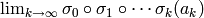 .
Given a set of substitutions
.
Given a set of substitutions  , we say that the representation is
, we say that the representation is
 -adic standard if the subtitutions are chosen in
-adic standard if the subtitutions are chosen in  .
.
INPUT:
OUTPUT:
A word.
EXAMPLES:
Let’s define three morphisms and compute the first nested succesive prefixes of the s-adic word:
sage: m1 = WordMorphism('e->gh,f->hg')
sage: m2 = WordMorphism('c->ef,d->e')
sage: m3 = WordMorphism('a->cd,b->dc')
sage: words.s_adic([m1],'e')
word: gh
sage: words.s_adic([m1,m2],'ec')
word: ghhg
sage: words.s_adic([m1,m2,m3],'eca')
word: ghhggh
When the given sequence of morphism is finite, one may simply give the last letter, i.e. 'a', instead of giving all of them, i.e. 'eca':
sage: words.s_adic([m1,m2,m3],'a')
word: ghhggh
sage: words.s_adic([m1,m2,m3],'b')
word: ghghhg
If the letters don’t satisfy the hypothesis of the algorithm (nested prefixes), an error is raised:
sage: words.s_adic([m1,m2,m3],'ecb')
...
ValueError: The hypothesis of the algorithm used is not satisfied: the image of the 3-th letter (=b) under the 3-th morphism (=WordMorphism: a->cd, b->dc) should start with the 2-th letter (=c).
Let’s define the Thue-Morse morphism and the Fibonacci morphism which will be used below to illustrate more examples and let’s import the repeat tool from the itertools:
sage: tm = WordMorphism('a->ab,b->ba')
sage: fib = WordMorphism('a->ab,b->a')
sage: from itertools import repeat
Two trivial examples of infinite s-adic words:
sage: words.s_adic(repeat(tm),repeat('a'))
word: abbabaabbaababbabaababbaabbabaabbaababba...
sage: words.s_adic(repeat(fib),repeat('a'))
word: abaababaabaababaababaabaababaabaababaaba...
A less trivial infinite s-adic word:
sage: t = words.ThueMorseWord([tm,fib])
sage: words.s_adic(t, repeat('a'))
word: abbaababbaabbaabbaababbaababbaabbaababba...
The same thing using a sequence of indices:
sage: tmword = words.ThueMorseWord([0,1])
sage: words.s_adic(tmword, repeat('a'), [tm,fib])
word: abbaababbaabbaabbaababbaababbaabbaababba...
The correspondance of the indices may be given as a dict:
sage: words.s_adic(tmword, repeat('a'), {0:tm,1:fib})
word: abbaababbaabbaabbaababbaababbaabbaababba...
because dict are more versatile for indices:
sage: tmwordTF = words.ThueMorseWord('TF')
sage: words.s_adic(tmwordTF, repeat('a'), {'T':tm,'F':fib})
word: abbaababbaabbaabbaababbaababbaabbaababba...
or by a callable:
sage: f = lambda n: tm if n == 0 else fib
sage: words.s_adic(words.ThueMorseWord(), repeat('a'), f)
word: abbaababbaabbaabbaababbaababbaabbaababba...
Random infinite s-adic words:
sage: from sage.misc.prandom import randint
sage: def it():
... while True: yield randint(0,1)
sage: words.s_adic(it(), repeat('a'), [tm,fib])
word: abbaabababbaababbaabbaababbaabababbaabba...
sage: words.s_adic(it(), repeat('a'), [tm,fib])
word: abbaababbaabbaababbaababbaabbaababbaabba...
sage: words.s_adic(it(), repeat('a'), [tm,fib])
word: abaaababaabaabaaababaabaaababaaababaabaa...
An example where the sequences cycle on two morphisms and two letters:
sage: G = WordMorphism('a->cd,b->dc')
sage: H = WordMorphism('c->ab,d->ba')
sage: from itertools import cycle
sage: words.s_adic([G,H],'ac')
word: cddc
sage: words.s_adic(cycle([G,H]),cycle('ac'))
word: cddcdccddccdcddcdccdcddccddcdccddccdcddc...
The morphism 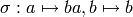 can’t satisfy the
hypothesis of the nested prefixes, but one may compute arbitrarily
long finite words having the limit
can’t satisfy the
hypothesis of the nested prefixes, but one may compute arbitrarily
long finite words having the limit 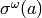 :
:
sage: sigma = WordMorphism('a->ba,b->b')
sage: words.s_adic(repeat(sigma),repeat('a'))
...
ValueError: The hypothesis of the algorithm used is not satisfied: the image of the 2-th letter (=a) under the 2-th morphism (=WordMorphism: a->ba, b->b) should start with the 1-th letter (=a).
sage: words.s_adic([sigma],'a')
word: ba
sage: words.s_adic([sigma,sigma],'a')
word: bba
sage: words.s_adic([sigma]*3,'a')
word: bbba
sage: words.s_adic([sigma]*4,'a')
word: bbbba
sage: words.s_adic([sigma]*5,'a')
word: bbbbba
sage: words.s_adic([sigma]*6,'a')
word: bbbbbba
sage: words.s_adic([sigma]*7,'a')
word: bbbbbbba
The following examples illustrates an  -adic word defined over an
infinite set
-adic word defined over an
infinite set  of morphisms
of morphisms 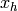 :
:
sage: x = lambda h:WordMorphism({1:[2],2:[3]+[1]*(h+1),3:[3]+[1]*h})
sage: for h in [0,1,2,3]: print h, x(h)
0 WordMorphism: 1->2, 2->31, 3->3
1 WordMorphism: 1->2, 2->311, 3->31
2 WordMorphism: 1->2, 2->3111, 3->311
3 WordMorphism: 1->2, 2->31111, 3->3111
sage: w = Word(lambda n : valuation(n+1, 2) ); w
word: 0102010301020104010201030102010501020103...
sage: s = words.s_adic(w, repeat(3), x); s
word: 3232232232322322322323223223232232232232...
sage: prefixe = s[:10000]
sage: map(prefixe.number_of_factors, range(15))
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
sage: [_[i+1] - _[i] for i in range(len(_)-1)]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
TESTS:
sage: tm = WordMorphism('a->ab,b->ba')
sage: fib = WordMorphism('a->ab,b->a')
sage: w = words.s_adic([fib,tm,tm,fib,tm,fib]*3,'a')
sage: w
word: abaaabaababaabaaababaaababaaabaababaabaa...
sage: w.length()
32400
sage: w.parent()
Words over Ordered Alphabet ['a', 'b']
sage: type(w)
<class 'sage.combinat.words.word.FiniteWord_iter_with_caching'>
sage: words.s_adic([fib,tm,tm,fib,tm,fib],'aaaaaaa')
word: abaaabaababaabaaababaaababaaabaababa
sage: words.s_adic([0,1,0,1,0,1,0,1],'a',[tm,fib])
word: abbaabababbaabbaababbaababbaabababbaabba...
sage: words.s_adic([fib,fib],'bb')
...
ValueError: The hypothesis of the algorithm used is not satisfied: the image of the 2-th letter (=b) under the 2-th morphism (=WordMorphism: a->ab, b->a) should start with the 1-th letter (=b).
Test on different letters:
sage: tm = WordMorphism({0:[0,1], 1:[1,0]})
sage: fib = WordMorphism({0:[0,1], 1:[0]})
sage: f = lambda n: tm if n == 0 else fib
sage: words.s_adic(words.ThueMorseWord(), repeat(0), f)
word: 0110010110011001100101100101100110010110...
Testing the message error for the third argument:
sage: words.s_adic(words.ThueMorseWord(), repeat(0), 5)
...
TypeError: morphisms (=5) must be None, callable or provide a __getitem__ method.
AUTHORS:
- Sebastien Labbe (2009-12-18): initial version
REFERENCES: