Combinatorial Species

This file defines the main classes for working with combinatorial species, operations on them, as well as some implementations of basic species required for other constructions.

This code is based on the work of Ralf Hemmecke and Martin Rubey’s Aldor-Combinat, which can be found at http://www.risc.uni-linz.ac.at/people/hemmecke/aldor/combinat/index.html. In particular, the relevant section for this file can be found at http://www.risc.uni-linz.ac.at/people/hemmecke/AldorCombinat/combinatse8.html.

Weighted Species:

As a first application of weighted species, we count unlabeled ordered trees by total number of nodes and number of internal nodes. To achieve this, we assign a weight of 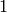to the leaves and of to internal nodes:

sage: q = QQ['q'].gen()
sage: leaf = species.SingletonSpecies()
sage: internal_node = species.SingletonSpecies(weight=q)
sage: L = species.LinearOrderSpecies(min=1)
sage: T = species.CombinatorialSpecies()
sage: T.define(leaf + internal_node*L(T))
sage: T.isotype_generating_series().coefficients(6)
[0, 1, q, q^2 + q, q^3 + 3*q^2 + q, q^4 + 6*q^3 + 6*q^2 + q]

Consider the following:

sage: T.isotype_generating_series().coefficient(4)
q^3 + 3*q^2 + q

This means that, among the trees on 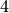nodes, one has a single internal node, three have two internal nodes, and one has three internal nodes.

class sage.combinat.species.species.GenericCombinatorialSpecies(min=None, max=None, weight=None)

Bases: sage.structure.sage_object.SageObject

algebraic_equation_system()

Returns a system of algebraic equations satisfied by this species. The nodes are numbered in the order that they appear as vertices of the associated digraph.

EXAMPLES:

sage: B = species.BinaryTreeSpecies()
sage: B.algebraic_equation_system()
[-node3^2 + node1, -node1 + node3 - z]

sage: B.digraph().vertices()
[Combinatorial species,
 Product of (Combinatorial species) and (Combinatorial species),
 Singleton species,
 Sum of (Singleton species) and (Product of (Combinatorial species) and (Combinatorial species))]

sage: B.algebraic_equation_system()[0].parent()
Multivariate Polynomial Ring in node0, node1, node2, node3 over Fraction Field of Univariate Polynomial Ring in z over Rational Field

composition(g)

EXAMPLES:

sage: S = species.SetSpecies()
sage: S(S)
Composition of (Set species) and (Set species)

cycle_index_series(*args, **kwds)

Returns the cycle index series for this species.

EXAMPLES:

sage: P = species.PermutationSpecies()
sage: g = P.cycle_index_series()
sage: g.coefficients(4)
[p[], p[1], p[1, 1] + p[2], p[1, 1, 1] + p[2, 1] + p[3]]

digraph()

Returns a directed graph where the vertices are the individual species that make up this one.

EXAMPLES:

sage: X = species.SingletonSpecies()
sage: B = species.CombinatorialSpecies()
sage: B.define(X+B*B)
sage: g = B.digraph(); g
Multi-digraph on 4 vertices

sage: g, labels = g.canonical_label(certify=True)
sage: list(sorted(labels.items()))
[(Combinatorial species, 0),
 (Product of (Combinatorial species) and (Combinatorial species), 2),
 (Singleton species, 1),
 (Sum of (Singleton species) and (Product of (Combinatorial species) and (Combinatorial species)), 3)]
sage: g.edges()
[(0, 3, None), (2, 0, None), (2, 0, None), (3, 1, None), (3, 2, None)]

functorial_composition(g)

Returns the functorial composition of self with g.

EXAMPLES:

sage: E = species.SetSpecies()
sage: E2 = E.restricted(min=2, max=3)
sage: WP = species.SubsetSpecies()
sage: P2 = E2*E
sage: G = WP.functorial_composition(P2)
sage: G.isotype_generating_series().coefficients(5)
[1, 1, 2, 4, 11]

generating_series(*args, **kwds)

Returns the generating series for this species. This is an exponential generating series so the nth coefficient of the series corresponds to the number of labeled structures with n labels divided by n!.

EXAMPLES:

sage: P = species.PermutationSpecies()
sage: g = P.generating_series()
sage: g.coefficients(4)
[1, 1, 1, 1]
sage: g.counts(4)
[1, 1, 2, 6]
sage: P.structures([1,2,3]).list()
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
sage: len(_)
6

is_weighted()

Returns True if this species has a nontrivial weighting associated with it.

EXAMPLES:

sage: C = species.CycleSpecies()
sage: C.is_weighted()
False

isotype_generating_series(*args, **kwds)

Returns the isotype generating series for this species. The nth coefficient of this series corresponds to the number of isomorphism types for the structures on n labels.

EXAMPLES:

sage: P = species.PermutationSpecies()
sage: g = P.isotype_generating_series()
sage: g.coefficients(4)
[1, 1, 2, 3]
sage: g.counts(4)
[1, 1, 2, 3]
sage: P.isotypes([1,2,3]).list()
[[2, 3, 1], [2, 1, 3], [1, 2, 3]]
sage: len(_)
3

isotypes(labels, structure_class=None)

EXAMPLES:

sage: F = CombinatorialSpecies()
sage: F.isotypes([1,2,3]).list()
...
NotImplementedError

product(g)

Returns the product of self and g.

EXAMPLES:

sage: P = species.PermutationSpecies()
sage: F = P * P; F
Product of (Permutation species) and (Permutation species)

restricted(min=None, max=None)

EXAMPLES:

sage: S = species.SetSpecies().restricted(min=3); S
Set species with min=3
sage: S.structures([1,2]).list()
[]
sage: S.generating_series().coefficients(5)
[0, 0, 0, 1/6, 1/24]

structures(labels, structure_class=None)

EXAMPLES:

sage: F = CombinatorialSpecies()
sage: F.structures([1,2,3]).list()
...
NotImplementedError

sum(g)

Returns the sum of self and g.

EXAMPLES:

sage: P = species.PermutationSpecies()
sage: F = P + P; F
Sum of (Permutation species) and (Permutation species)
sage: F.structures([1,2]).list()
[[1, 2], [2, 1], [1, 2], [2, 1]]

weight_ring()

Returns the ring in which the weights of this species occur.

By default, this is just the field of rational numbers.

EXAMPLES:

sage: species.SetSpecies().weight_ring()
Rational Field

weighted(weight)

Returns a version of this species with the specified weight.

EXAMPLES:

sage: t = ZZ['t'].gen()
sage: C = species.CycleSpecies(); C
Cyclic permutation species
sage: C.weighted(t)
Cyclic permutation species with weight=t