CoalgebrasWithBasis

class sage.categories.coalgebras_with_basis.CoalgebrasWithBasis(base, name=None)

Bases: sage.categories.category_types.Category_over_base_ring

The category of coalgebras with a distinguished basis

EXAMPLES:

sage: CoalgebrasWithBasis(ZZ)
Category of coalgebras with basis over Integer Ring
sage: CoalgebrasWithBasis(ZZ).super_categories()
[Category of modules with basis over Integer Ring, Category of coalgebras over Integer Ring]

TESTS:

sage: TestSuite(CoalgebrasWithBasis(ZZ)).run()

class ElementMethods

class CoalgebrasWithBasis.ParentMethods

coproduct()

If coproduct_basis() is available, construct the coproduct morphism from self to self 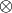self by extending it by linearity

EXAMPLES:

sage: A = HopfAlgebrasWithBasis(QQ).example(); A
An example of Hopf algebra with basis: the group algebra of the Dihedral group of order 6 as a permutation group over Rational Field
sage: [a,b] = A.algebra_generators()
sage: a, A.coproduct(a)
(B[(1,2,3)], B[(1,2,3)] # B[(1,2,3)])
sage: b, A.coproduct(b)
(B[(1,3)], B[(1,3)] # B[(1,3)])

CoalgebrasWithBasis.super_categories(*args, **kwds)

EXAMPLES:

sage: CoalgebrasWithBasis(QQ).super_categories()
[Category of modules with basis over Rational Field, Category of coalgebras over Rational Field]