In Sage, we can create the number field
![\QQ(\sqrt[3]{2})](_images/math/c79d00be2051541ca454120136c786792a8bde88.png) as follows.
as follows.
sage: K.<alpha> = NumberField(x^3 - 2)
The above creates two Sage objects, 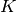 and
and
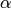 . Here
. Here 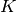 “is” (isomorphic to) the number
field
“is” (isomorphic to) the number
field ![\QQ(\sqrt[3]{2})](_images/math/c79d00be2051541ca454120136c786792a8bde88.png) , as we confirm below:
, as we confirm below:
sage: K
Number Field in alpha with defining polynomial x^3 - 2
and 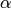 is a root of
is a root of 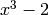 , so
, so
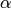 is an abstract choice of
is an abstract choice of ![\sqrt[3]{2}](_images/math/9fdfe572d1673f00f286d5ed753942d18f401cbb.png) (no
specific embedding of the number field
(no
specific embedding of the number field 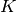 into
into
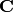 is chosen by default in Sage-3.1.2):
is chosen by default in Sage-3.1.2):
sage: alpha^3
2
sage: (alpha+1)^3
3*alpha^2 + 3*alpha + 3
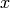 ¶
¶Note that we did not define 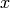 above before using it.
You could “break” the above example by redefining
above before using it.
You could “break” the above example by redefining 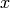 to be
something funny:
to be
something funny:
sage: x = 1
sage: K.<alpha> = NumberField(x^3 - 2)
...
TypeError: polynomial (=-1) must be a polynomial.
The Traceback above indicates that there was an error. Potentially lots of detailed information about the error (a “traceback”) may be given after the word Traceback and before the last line, which contains the actual error messages.
Note
Important: whenever you use Sage and get a big error, look at the last line for the actual error, and only look at the rest if you are feeling adventurous. In the notebook, the part indicated by ... above is not displayed; to see it, click just to the left of the word Traceback and the traceback will appear.
If you redefine 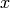 as above, but need to define a number
field using the indeterminate
as above, but need to define a number
field using the indeterminate 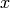 , you have several
options. You can reset
, you have several
options. You can reset 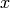 to its default value at the
start of Sage, you can redefine
to its default value at the
start of Sage, you can redefine 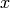 to be a symbolic
variable, or you can define
to be a symbolic
variable, or you can define 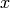 to be a polynomial
indeterminate (a polygen):
to be a polynomial
indeterminate (a polygen):
sage: reset('x')
sage: x
x
sage: x = 1
sage: x = var('x')
sage: x
x
sage: x = 1
sage: x = polygen(QQ, 'x')
sage: x
x
sage: x = 1
sage: R.<x> = PolynomialRing(QQ)
sage: x
x
One you have created a number field 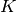 , type K.[tab key] to
see a list of functions. Type, e.g., K.Minkowski_embedding?[tab
key] to see help on the Minkowski_embedding command. To see
source code, type K.Minkowski_embedding??[tab key].
, type K.[tab key] to
see a list of functions. Type, e.g., K.Minkowski_embedding?[tab
key] to see help on the Minkowski_embedding command. To see
source code, type K.Minkowski_embedding??[tab key].
sage: K.<alpha> = NumberField(x^3 - 2)
sage: K.[tab key]
Another natural way for us to create certain number fields is to
create a symbolic expression and adjoin it to the rational
numbers. Unlike Pari and Magma (and like Mathematica and Maple), Sage
also supports manipulation of symbolic expressions and solving
equations, without defining abstract structures such as a number
fields. For example, we can define a variable 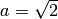 as an
abstract symbolic object by simply typing a = sqrt(2). When we
type parent(a) below, Sage tells us the mathematical object that
it views
as an
abstract symbolic object by simply typing a = sqrt(2). When we
type parent(a) below, Sage tells us the mathematical object that
it views  as being an element of; in this case, it’s the ring
of all symbolic expressions.
as being an element of; in this case, it’s the ring
of all symbolic expressions.
sage: a = sqrt(2)
sage: parent(a)
Symbolic Ring
In particular, typing sqrt(2) does not numerically extract an
approximation to 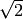 , like it would in Pari or Magma. We
illustrate this below by calling Pari (via the gp interpreter) and
Magma directly from within Sage. After we evaluate the following two
input lines, copies of GP/Pari and Magma are running, and there is a
persistent connection between Sage and those sessions.
, like it would in Pari or Magma. We
illustrate this below by calling Pari (via the gp interpreter) and
Magma directly from within Sage. After we evaluate the following two
input lines, copies of GP/Pari and Magma are running, and there is a
persistent connection between Sage and those sessions.
sage: gp('sqrt(2)')
1.414213562373095048801688724...
sage: magma('Sqrt(2)') # optional - magma
1.414213562373095048801688724...
You probably noticed a pause when evaluated the second line as Magma started up. Also, note the # optional comment, which indicates that the line won’t work if you don’t have Magma installed.
Incidentally, if you want to numerically evaluate 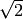 in
Sage, just give the optional prec argument to the sqrt
function, which takes the required number of bits (binary digits)
of precision.
in
Sage, just give the optional prec argument to the sqrt
function, which takes the required number of bits (binary digits)
of precision.
sage: sqrt(2, prec=100)
1.4142135623730950488016887242
It’s important to note in computations like this that there is not an
a priori guarantee that prec bits of the answer are all
correct. Instead, what happens is that Sage creates the number
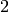 as a floating point number with
as a floating point number with 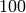 bits of
accuracy, then asks Paul Zimmerman’s MPFR C library to compute the
square root of that approximate number.
bits of
accuracy, then asks Paul Zimmerman’s MPFR C library to compute the
square root of that approximate number.
We return now to our symbolic expression 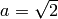 . If
you ask to square
. If
you ask to square 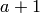 you simply get the formal square.
To expand out this formal square, we use the expand command.
you simply get the formal square.
To expand out this formal square, we use the expand command.
sage: a = sqrt(2)
sage: (a+1)^2
(sqrt(2) + 1)^2
sage: expand((a+1)^2)
2*sqrt(2) + 3
Given any symbolic expression for which Sage can computes its
minimal polynomial, you can construct the number field obtained by
adjoining that expression to 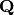 . The notation is
quite simple - just type QQ[a] where a is the symbolic expression.
. The notation is
quite simple - just type QQ[a] where a is the symbolic expression.
sage: a = sqrt(2)
sage: K.<b> = QQ[a]
sage: K
Number Field in sqrt2 with defining polynomial x^2 - 2
sage: b
sqrt2
sage: (b+1)^2
2*sqrt2 + 3
sage: QQ[a/3 + 5]
Number Field in a with defining polynomial x^2 - 10*x + 223/9
You can’t create the number field 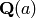 in Sage by
typing QQ(a), which has a very different meaning in Sage. It
means “try to create a rational number from
in Sage by
typing QQ(a), which has a very different meaning in Sage. It
means “try to create a rational number from  .” Thus QQ(a)
in Sage is the analogue of QQ!a in Magma (Pari has no notion of
rings such as QQ).
.” Thus QQ(a)
in Sage is the analogue of QQ!a in Magma (Pari has no notion of
rings such as QQ).
sage: a = sqrt(2)
sage: QQ(a)
...
TypeError: unable to convert sqrt(2) to a rational
In general, if 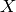 is a ring, or vector space or other “parent
structure” in Sage, and
is a ring, or vector space or other “parent
structure” in Sage, and  is an element, type X(a) to
make an element of
is an element, type X(a) to
make an element of 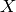 from
from  . For example, if
. For example, if 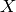 is the finite field of order
is the finite field of order 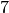 , and
, and 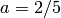 is a
rational number, then X(a) is the finite field element
is a
rational number, then X(a) is the finite field element 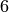 (as a quick exercise, check that this is mathematically the correct
interpretation).
(as a quick exercise, check that this is mathematically the correct
interpretation).
sage: X = GF(7); a = 2/5
sage: X(a)
6
As a slightly less trivial illustration of symbolic manipulation, consider the cubic equation
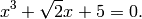
In Sage, we can create this equation, and find an exact symbolic solution.
sage: x = var('x')
sage: eqn = x^3 + sqrt(2)*x + 5 == 0
sage: a = solve(eqn, x)[0].rhs()
The first line above makes sure that the symbolic variable 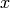 is defined, the second creates the equation eqn, and the third
line solves eqn for
is defined, the second creates the equation eqn, and the third
line solves eqn for 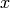 , extracts the first solution (there
are three), and takes the right hand side of that solution and assigns
it to the variable a.
, extracts the first solution (there
are three), and takes the right hand side of that solution and assigns
it to the variable a.
To see the solution nicely typeset, use the show command
sage: show(a)
-\frac{1}{2} ...
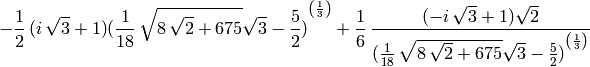
You can also see the latex needed to paste  into a paper
by typing latex(a). The latex
command works on most Sage objects.
into a paper
by typing latex(a). The latex
command works on most Sage objects.
sage: latex(a)
-\frac{1}{2} \, {\left(i \, \sqrt{3} + 1\right)} ...
Next, we construct the number field obtained by adjoining the solution
a to 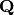 . Notice that the minimal polynomial of the
root is
. Notice that the minimal polynomial of the
root is 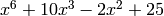 .
.
Warning
The following tests are currently broken until Trac ticket #5338 is fixed.
sage: K.<b> = QQ[a]
sage: K
Number Field in a with defining
polynomial x^6 + 10*x^3 - 2*x^2 + 25
sage: a.minpoly()
x^6 + 10*x^3 - 2*x^2 + 25
sage: b.minpoly()
x^6 + 10*x^3 - 2*x^2 + 25
We can now compute interesting invariants of the number field
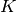
sage: K.class_number()
5
sage: K.galois_group().order()
72