Bibliography

1

Biler, P., Local and global solvability of some parabolic systems modelling chemotaxis, Adv. Math. Sci. Appl., 8 (1998) 715-743.

2

Childress, S. and Percus, J. K., Nonlinear aspects of chemotaxis, Math. Biosci., 56 (1981), 217-237.

3

Diaz, J. I., Nagai, T. and Rakotoson, J. M., Symmetrization techniques on unbounded domains: Application to a chemotaxis system on 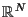${\mathbb{R}}^N$, J. Differential Equations, 145 (1998), 156-183.

4

Gajewski, H. and Zacharias, K., Global behavior of a reaction-diffusion system modelling chemotaxis, Math. Nachr., 195 (1998), 77-114.

5

Harada, G., Nagai, T., Senba, T. and Suzuki, T., Concentration lemma, Brezis-Merle type inequality, and a parabolic system of chemotaxis, Advances in Differential Equations, 6 (2001), 1255-1280.

6

Henry, D., Geometric Theory of Semilinear Parabolic Equations, Lecture Note in Math., 840, Springer, 1981.

7

Herrero, M. A. and Velázquez, J. J. L., A blow-up mechanism for a chemotactic model, Ann. Scuola Normale Sup. Pisa, XXIV (1997), 633-683.

8

Horstmann, D. and Wang, G., Blow-up in a chemotaxis model without symmetry assumptions, Euro. Jnl of Applied Mathematics, 12(2001), 159-177.

9

Jäger, W. and Luckhaus, S., On explosions of solutions to a system of partial differential equations modelling chemotaxis, Trans. Amer. Math. Soc., 329 (1992), 819-824.

10

Keller, E. F. and Segel, L. A., Initiation of slime mold aggregation viewed as an instability, J. Theor. Biol., 26 (1970), 399-415.

11

Ladyzhenskaya, O. A., Solonnikov, V. A. and Uralt'seva, N. N., Linear and Quasi-linear Equations of Parabolic Type, Nauka, Moscow, 1967: English translation: Amer. Math. Soc., Providence, R. I., 1968.

12

Nagai, T., Behavior of solutions to a parabolic-elliptic system modelling chemotaxis, J. Korean Math. Soc., 37 (2000), 721-733.

13

Nagai, T., Blowup of nonradial solutions to parabolic-elliptic systems modeling chemotaxis in two-dimensional domains, J. of Inequal. & Appl., 6 (2001), 37-55.

14

Nagai, T., Global existence and blowup of solutions to a chemotaxis system, Proceedings of the Second World Congress of Nonlinear Analysis(Athens, 2000), Nonlinear Anal. 47 (2001), 777-787.

15

Nagai, T., Senba, T. and Suzuki, T., Chemotactic collapse in a parabolic system of mathematical biology, Hiroshima Math. J., 30 (2000), 463-497.

16

Nagai, T., Senba, T. and Yoshida, K., Application of the Trudinger-Moser inequality to a parabolic system of chemotaxis, Funkcialaj Ekvacioj, 40(1997), 411-433.

17

Nanjundiah, V., Chemotaxis, signal relaying, and aggregation morphology, J. Theor. Biol., 42 (1973), 63-105.

18

Senba, T. and Suzuki, T., Chemotactic collapse in a parabolic-elliptic system of mathematical biology, Advances in Differential Equations, 6 (2000), 21-50.

19

Yagi, A., Norm behavior of solutions to the parabolic system of chemotaxis, Math. Japonica, 45 (1997), 241-265.