next up previous
: Bibliography : Decay Properties and Asymptotic : Decay Properties and Asymptotic

Introduction

In this paper, we study the large time behavior of bounded solutions to the Cauchy problem for the following system of partial differential equations in $ {\mathbb{R}}^n$, $ n\ge 2$:

(1.1)   $\displaystyle \frac{\partial u}{\partial t}=\nabla\cdot(\nabla u-u\nabla v),$ $\displaystyle x\in{\mathbb{R}}^n, \ t>0,$
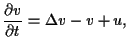(1.2)   $\displaystyle \frac{\partial v}{\partial t}=\Delta v-v+u,$ $\displaystyle x\in{\mathbb{R}}^n, \ t>0,$
(1.3)   $\displaystyle u(x,0)=u_0,\quad v(x,0)=v_0,$ $\displaystyle x\in{\mathbb{R}}^n.$

The system (1.1), (1.2) is a mathematical model describing chemotaxis, that is, the directed movement of an organism in response to gradients of a chemical attractant(see [2,10,17]). $ u(x,t)$ corresponds to the population of the organism at place $ x$ and time $ t$, and $ v(x,t)$ to the concentration of the chemical.

Throughout this paper, it is always assumed that

    $\displaystyle u_0, \ v_0, \ \partial_jv_0 \in L^1({\mathbb{R}}^n)\cap{\cal B}({\mathbb{R}}^n) \ (1\le j\le n).$

Here, we use the notation $ \partial_j=\partial/\partial x_j$ for simplicity, and $ {\cal B}({\mathbb{R}}^n)$ is the Banach space of all bounded and uniformly continuous functions on $ {\mathbb{R}}^n$ with the usual supremum norm. We write (1.1)-(1.3) in the form of the integral equation:

(1.4) $\displaystyle u(t)=$ $\displaystyle e^{t\Delta}u_0 - \int_0^t \nabla\cdot e^{(t-s)\Delta}(u\nabla v)(s)ds,$
(1.5) $\displaystyle v(t)=$ $\displaystyle e^{-t}e^{t\Delta}v_0 + \int_0^t e^{-t+s}e^{(t-s)\Delta}u(s)ds,$

where

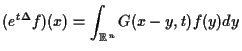    $\displaystyle (e^{t\Delta}f)(x)=\int_{{\mathbb{R}}^n} G(x-y,t)f(y)dy$

and $ G(x,t)$ is the heat kernel

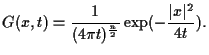    $\displaystyle G(x,t)=\frac{1}{(4\pi t)^{\frac{n}{2}}}\exp (-\frac{\vert x\vert^2 }{4t}).$

A function $ (u(x,t), v(x,t))$ on $ {\mathbb{R}}^n\times [0, T] \ (0<T<\infty)$ is said to be a solution of (1.1)-(1.3) on $ {\mathbb{R}}^n\times [0, T]$ if

    $\displaystyle u, \ v, \ \partial_jv \in C([0, T] : L^1({\mathbb{R}}^n))\cap C([0, T] : {\cal B}({\mathbb{R}}^n)) \quad (1\le j\le n)$

and $ (u, v)$ satisfies (1.4), (1.5) on $ [0, T]$. It is also said that $ (u, v)$ is a solution of (1.1)-(1.3) on $ {\mathbb{R}}^n \times [0,\infty)$ if $ (u, v)$ is a solution of (1.1)-(1.3) on $ {\mathbb{R}}^n\times [0, T]$ for every $ 0<T<\infty$. Using standard regularity arguments for the heat equation(see Chapter IV of [11]), we see that $ (u, v)$ is a classical solution of (1.1)-(1.3), which satisfies

$\displaystyle u, v \in C((0, T): W^{2,p}({\mathbb{R}}^n))\cap C^1((0, T): L^p({\mathbb{R}}^n))$   for every $\displaystyle \ 1<p<\infty.$

It is shown in [14] that every bounded solution of (1.1)-(1.3) on $ {\mathbb{R}}^2\times [0, \infty)$ decays to zero as $ t\to\infty$ and behaves like the heat kernel. We give the large time behavior for higher dimensional case in the following theorem. In what follows, $ \Vert\cdot\Vert _p$ represents the usual $ L^p$-norm.

Theorem 1.1   Let $ (u, v)$ be a solution of (1.1)-(1.3) on $ {\mathbb{R}}^n \times [0,\infty)$ and $ n\ge 2$. Suppose that

(1.6) $\displaystyle \sup_{t>0} \bigl( \Vert u(t)\Vert _p + \Vert v(t)\Vert _p \bigr)<\infty$   for $\displaystyle p=1, \infty.$

Then, for every $ 1<p\le \infty$,

      $\displaystyle \sup_{t>0} (1+t)^{n(1-1/p)/2}\bigl( \Vert u(t)\Vert _p + \Vert v(t)\Vert _p \bigr)< \infty,$
      $\displaystyle \lim_{t\to\infty} t^{n(1-1/p)/2}\Big\Vert u(t)- \int_{{\mathbb{R}}^n}u_0\,dy G(t)\Big\Vert _p=0,$
      $\displaystyle \lim_{t\to\infty} t^{n(1-1/p)/2}\Big\Vert v(t)- \int_{{\mathbb{R}}^n}u_0\,dy G(t)\Big\Vert _p=0.$

For nonnegative solutions of (1.1)-(1.3), we need (1.6) only for $ p=\infty$, because integrating (1.4) and (1.5) on $ {\mathbb{R}}^n$ respectively, we observe that

    $\displaystyle \Vert u(t)\Vert _1= \Vert u_0\Vert _1,\quad \Vert v(t)\Vert _1= e^{-t}\Vert v_0\Vert _1 + (1- e^{-t})\Vert u_0\Vert _1.$

Concerning the existence of bounded solutions, it is possible for a nonnegative solution of (1.1)-(1.3) in $ {\mathbb{R}}^n (n\ge 2)$ to blow up in finite time(see [2]). For a simplified version of (1.1)-(1.2) replaced (1.2) by $ 0=\Delta v -v + u$ in $ {\mathbb{R}}^2$, it is shown that the nonnegative solution exists globally in time under the condition $ \int_{{\mathbb{R}}^2} u_0\,dx<8\pi$(see [3]), and that the finite-time blowup of nonnegative solutions may occur under the condition $ \int_{{\mathbb{R}}^2} u_0\,dx>8\pi$(see [3,12]). It is also shown in [12] that the finite-time blowup of nonnegative solutions in $ {\mathbb{R}}^n (n\ge 3)$ may occur even if $ \int_{{\mathbb{R}}^n} u_0\,dx$ is small. For blowup problems to (1.1), (1.2) in a bounded domain, we refer to [1,4,5,7,8,9,13,15,16,18,19] and the references therein.

The following theorem gives the existence of bounded solutions to (1.1)-(1.3) in $ {\mathbb{R}}^n, n\ge 2$, when $ \Vert u_0\Vert _1, \Vert\nabla v_0\Vert _1, \Vert\nabla v_0\Vert _\infty$ are small but $ \Vert u_0\Vert _\infty$ is not necessarily small. The uniqueness of solutions is also given in the theorem. The nonnegativity of solutions is not assumed.

Theorem 1.2   (i) The uniqueness of solutions to (1.1)-(1.3) holds.

(ii) Let $ n\ge 2$. For any given $ K>0$ let $ (u_0, v_0)$ be an initial function satisfying

    $\displaystyle \Vert u_0\Vert _\infty \le K.$

Then there exists a small $ \delta>0$, depending on $ K$, such that (1.1)-(1.3) admits a solution on $ {\mathbb{R}}^n \times [0,\infty)$ satisfying (1.6), provided that

    $\displaystyle \Vert u_0\Vert _1 \le\delta, \ \Vert\nabla v_0\Vert _1 \le\delta, \ \Vert\nabla v_0\Vert _\infty \le\delta.$

next up previous
: Bibliography : Decay Properties and Asymptotic : Decay Properties and Asymptotic
Nobuki Takayama Heisei 16-1-21.