| (1.1) | 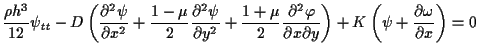 |
in | |
| (1.2) | 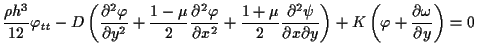 |
in | |
| (1.3) | ![$\displaystyle \rho h \omega_{tt} - K\left[ { \frac{\partial }{\partial x}\left(...
... y}\left( {\varphi + \frac{\partial {\omega}}{\partial y} } \right) } \right]=0$](img9.png) |
in |

We assume that the plate is clamped along ![]() , that is
, that is
![$\displaystyle D\left[ { \nu_1\frac{\partial {\psi}}{\partial x}+\mu\nu_1\frac{\...
...i}}{\partial y}+\frac{\partial {\varphi}}{\partial x}} \right)\nu_2 } \right] ,$](img27.png) | |||
![$\displaystyle D\left[ { \nu_2\frac{\partial {\varphi}}{\partial y}+\mu\nu_2\fra...
...i}}{\partial y}+\frac{\partial {\varphi}}{\partial x}} \right)\nu_1 } \right] ,$](img29.png) | |||
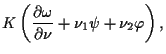 |
Concerning memory condition on the boundary we can cite only a few works. In [1] Ciarletta established theorems of existence, uniqueness and asymptotic stability for a linear model of heat conduction. In this case the memory condition describes a boundary that can absorb heat and due to the hereditary term, can retain part of it. In [2] Fabrizio and Morro consider a linear electromagnetic model and proved the existence, uniqueness and asymptotic stability of the solutions. In [6] Muñoz Rivera and Andrade showed exponential stability for a non homogeneous anisotropic system when the resolvent kernel of the memory is exponential type. Polynomial resolvent kernel was not considered in that work.
The nonlinear one-dimensional wave equation with memory condition on
the boundary was studied by Qin [7], he showed existence,
uniqueness and stability of global solutions provided the initial
data is small in
![]() , this result was improved by
Muñoz Rivera and Andrade [5], by taking small
initial data in
, this result was improved by
Muñoz Rivera and Andrade [5], by taking small
initial data in
![]() .
.
The uniform stabilization of system (1.1)-(1.4) for frictional boundary conditions instead of condition (1.5) was studied by Lagnese [3], who proved, under some geometrical conditions that the energy associated to the Mindlin-Timoshenko's plate decays exponentially as time goes to infinity.
The aim of this paper is to study the asymptotic behavior of solutions of
system (1.1)-(1.6). We show that the
solution decays exponentially to zero provided the relaxation
functions ![]() decays exponentially
to zero. Moreover, if
decays exponentially
to zero. Moreover, if ![]() decays polynomially, then we show that the
corresponding solution also decays polynomially to zero with the
same rate of decay.
decays polynomially, then we show that the
corresponding solution also decays polynomially to zero with the
same rate of decay.
The remainder part of this paper is organized as follows. In the next section we establish the existence, uniqueness and regularity of solutions. In section 3 we show the exponential decay of the first order energy and finally, in section 4 we prove the polynomial decay.