


: Bibliography
: Lower Estimates for the
: Lower Estimates for the
Consider the first and the second Painlevé equations
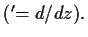 All the solutions of
these equations are meromorphic in the whole complex
plane
All the solutions of
these equations are meromorphic in the whole complex
plane 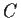 ([5], [9]).
Every solution of (I) is transcendental, and equation
(II)
([5], [9]).
Every solution of (I) is transcendental, and equation
(II)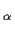 admits a rational solution if and only if
admits a rational solution if and only if
 $Z$
(e.g. [2], [8]); these equations
define Painlevé transcendents.
$Z$
(e.g. [2], [8]); these equations
define Painlevé transcendents.
The growth of a meromorphic function 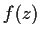 is measured
by the characteristic function defined by
is measured
by the characteristic function defined by
with
here 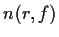 denotes the number of poles in
denotes the number of poles in
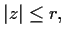 each counted according to its multiplicity
(for the notation of value distribution theory and basic
facts, see [4], [6]). Also we use the notation
each counted according to its multiplicity
(for the notation of value distribution theory and basic
facts, see [4], [6]). Also we use the notation
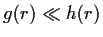 if
if
 as
as

The growth of each Painlevé transcendent is
estimated as follows ([10], [11]):
Theorem A.
Let 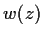 be an arbitrary solution of (I)
be an arbitrary solution of (I)
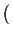 resp. (II)
resp. (II)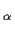
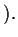 Then,
Then,
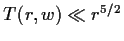
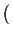 resp.
resp.
 On the other hand,
Mues and Redheffer [7] have shown the following:
Theorem B.
For every solution
On the other hand,
Mues and Redheffer [7] have shown the following:
Theorem B.
For every solution 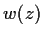 of (I), we have
of (I), we have
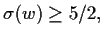 where
where
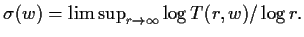 By these results, the order of the first Painlevé
transcendents is
By these results, the order of the first Painlevé
transcendents is 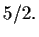
In this paper we improve on the result of Theorem B, and
under a certain condition, we give a lower estimate for
 of the second Painlevé transcendents.
Our results are stated as follows:
of the second Painlevé transcendents.
Our results are stated as follows:
Theorem 1.1
For every solution 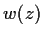 of
of (I)
, we have
An arbitrary solution of (I) is expressible in the form
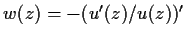 , where
, where 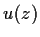 is an entire function
called a
is an entire function
called a 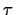 -function. Note that it
is uniquely determined apart from
the factor
-function. Note that it
is uniquely determined apart from
the factor
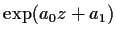
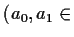 $C$
$C$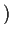 .
.
Theorem 1.2
For every solution of (I)
, its 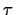 -function
-function
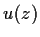 satisfies
satisfies
Remark 1.1
The implicit coefficients of the relation in Theorem 1.1 are
estimated as follows:
where

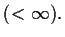
Remark 1.2
For every solution
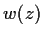
of (I), Boutroux
[
1] asserts the inequality
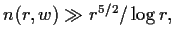
but his proof contains an incorrect
part.
Remark 1.3
If
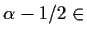 $Z$
$Z$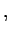
then equation
(II)
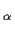
admits a one-parameter family of solutions
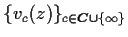
such that
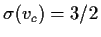
(see Section 4.3 and [
2]).



: Bibliography
: Lower Estimates for the
: Lower Estimates for the
Nobuki Takayama
Heisei 15-9-23.
![]() is measured
by the characteristic function defined by
is measured
by the characteristic function defined by
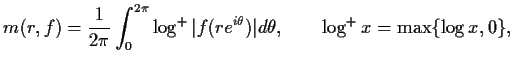

![]() be an arbitrary solution of (I)
be an arbitrary solution of (I)
![]() resp. (II)
resp. (II)![]()
![]() Then,
Then,
![]()
![]() resp.
resp.
![]() On the other hand,
Mues and Redheffer [7] have shown the following:
Theorem B.
For every solution
On the other hand,
Mues and Redheffer [7] have shown the following:
Theorem B.
For every solution ![]() of (I), we have
of (I), we have
![]() where
where
![]() By these results, the order of the first Painlevé
transcendents is
By these results, the order of the first Painlevé
transcendents is ![]()
![]() of the second Painlevé transcendents.
Our results are stated as follows:
of the second Painlevé transcendents.
Our results are stated as follows: