Bibliography

1

K. Aomoto, On the structure of integrals of power products of linear functions, Sci. Papers, Coll. Gen. Education, Univ. of Tokyo, 27 (1977), 49-61.

2

K. Aomoto, Special value of the hypergeometric function 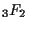${_3F_2}$ and connection formulae among asymptotic expansions, J. Indian Math. Soc., 51 (1987), 161-221.

3

W. Balser, Explicit evaluation of the Stokes' multipliers and central connection coefficients for certain systems of linear differential equations, Math. Nachr., 138 (1988), 131-144.

4

W. Balser, W. B. Jurkat and D. A. Lutz, Birkhoff invariants and Stokes' multipliers for meromorphic linear differential equations, J. Math. Anal. Appl., 71 (1979), 48-94.

5

W. Balser, W. B. Jurkat and D. A. Lutz, On the reduction of connection problems for differential equations with an irregular singular point to ones with only regular singularities, I, SIAM J. Math. Anal., 12 (1981), 691-721.

6

W. Balser, W. B. Jurkat and D. A. Lutz, On the reduction of connection problems for differential equations with an irregular singular point to ones with only regular singularities, II, SIAM J. Math. Anal., 19 (1988), 398-443.

7

G. D. Birkhoff, Singular points of ordinary linear differential equations, Trans. Amer. Math. Soc., 10 (1909), 436-470.

8

Y. Haraoka, Canonical forms of differential equations free from accessory parameters, SIAM J. Math. Anal., 25 (1994), 1203-1226.

9

Y. Haraoka, Monodromy representations of systems of differential equations free from accessory parameters, ibid. 25 (1994), 1595-1621.

10

Y. Haraoka, Irreducibility of accessory parameter free systems, Kumamoto J. Math., 8 (1995), 153-170.

11

Y. Haraoka, Integral representations of solutions of differential equations free from accessory parameters, Adv. Math., 169 (2002), 187-240.

12

M. Hukuhara, Sur les points singuliers des équations différentielles linéaires, III, Mem. Fac. Sci. Kyusyu Imp. Univ., 2 (1941), 125-137.

13

M. Hukuhara, ``Ordinary differential equations'', Second Edition, Iwanami Shoten, 1980 (in Japanese).

14

N. M. Katz, ``Rigid Local Systems'', Princeton Univ. Press, 1996.

15

Y. L. Luke, ``The Special Functions and Their Approximations'', Vol. I, Academic Press, New York and London, 1969.

16

K. Matsumoto, T. Sasaki, N. Takayama and M. Yoshida, Monodromy of the hypergeometric differential equation of type (3,6), I, Duke Math. J., 71 (1993), 403-426.

17

K. Mimachi, An integral representation of the solution of a fourth order Fuchsian differential equation of Okubo type, Funk. Ekvac., 38 (1995), 411-416.

18

K. Okubo, Connction problems for systems of linear differential equaitons, in ``Japan-United States Seminar on Ordinary Differential Equations (Kyoto, 1971)'', pp. 238-248. Lecture Notes in Math., 243, Springer, Berlin, 1971.

19

K. Okubo, ``On the group of Fuchsian equations'', Seminar Reports of Tokyo Metropolitan University, Tokyo, 1987.

20

T. Sasai and S. Tsuchiya, On a fourth order Fuchsian differential equation of Okubo type, Funk. Ekvac., 34 (1991), 211-221.

21

T. Yokoyama, On an irreducibility condition for hypergeometric systems, Funk. Ekvac., 38 (1995), 11-19.