


: Bibliography
: Evaluation of Stokes multipliers
: Evaluation of Stokes multipliers
In [5] Balser, Jurkat and Lutz studied a system of linear differential
equations of Birkhoff canonical form of Poincaré rank one, i.e.
where 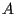 is a constant
is a constant 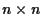 matrix and
matrix and
![$\Lambda={\rm diag}[\lambda_1,\dots,\lambda_n]$](img4.png) .
Under the assumuption that
.
Under the assumuption that
 has all distinct diagonal elements,
they showed
that the Stokes multipliers for (0.1) can be expressed by using the connection
coefficients for the associated system of linear differential equations
has all distinct diagonal elements,
they showed
that the Stokes multipliers for (0.1) can be expressed by using the connection
coefficients for the associated system of linear differential equations
which is Fuchsian and has regular singular points
 .
Balser [3] studied the same problem for the system (0.1) with
.
Balser [3] studied the same problem for the system (0.1) with
![$\Lambda={\rm diag}[0,\dots,0,1]$](img8.png) whose associated system (0.2) is equivalent
to the differential equation satisfied by the generalized hypergeometric
series
whose associated system (0.2) is equivalent
to the differential equation satisfied by the generalized hypergeometric
series 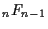 ,
and evaluated the Stokes multipliers for (0.1) explicitly.
As Balser's result suggests, we do not need the assumption that
,
and evaluated the Stokes multipliers for (0.1) explicitly.
As Balser's result suggests, we do not need the assumption that
 has all distinct diagonal elements
to establish the relation
between the Stokes multipliers for (0.1) and the connection coefficients
for (0.2) (Theorem 5.2).
Then the essential part of his result is the evaluation of the connection
coefficients for the associated system.
has all distinct diagonal elements
to establish the relation
between the Stokes multipliers for (0.1) and the connection coefficients
for (0.2) (Theorem 5.2).
Then the essential part of his result is the evaluation of the connection
coefficients for the associated system.
Recently we have shown that, if the monodromy representation of the system
(0.2)
defines a rigid local system
(we call such a system (0.2) rigid),
the solutions of the system have an integral representation ([11]).
Then, for rigid systems, by using the integral representation we can evaluate
the connection coefficients and hence the Stokes multipliers for the
corresponding system (0.1).
(Note that Balser's system (0.2) is also rigid.)
In this paper we take a rigid system of rank 4 whose solution can be
represented by a double integral,
evaluate the connection coefficients by using the integral,
and evaluate the Stokes multipliers for the corresponding system (0.1).
It seems hard to describe the connection coefficients for
a general rigid system;
however, the computation in this paper will be applied to each rigid system.



: Bibliography
: Evaluation of Stokes multipliers
: Evaluation of Stokes multipliers
Nobuki Takayama
Heisei 15-9-23.