Bibliography

1

Dolgachev, I. and Ortland, D., Point sets in projective spaces and theta functions, Astérisque Soc.Math.de France, 165(1988)

2

Grammaticos, B., Ramani, A. and Papageorgiou, V., Do integrable mappings have the Painlevé property?, Phys. Rev. Lett., 67(1991), 1825-1827

3

Jimbo, M. and Sakai, H., A q-analog of the sixth Painlevé equation, Lett. Math. Phys., 38(1996), 145-154

4

Kac, V., Infinite dimensional Lie algebras 3rd edn, Cambridge: Cambridge University Press(1990)

5

Kajiwara K., Noumi, M. and Yamada, Y., A study on the fourth 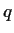$q$-Painlevé equation, J. Phys. A, 34(2001), 8563-8581

6

Kajiwara K., Noumi, M. and Yamada, Y., Discrete dynamical systems with 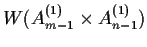$W(A^{(1)}_{m-1} \times A^{(1)}_{n-1})$ symmetry, preprint nlin.SI/0106029 (2001)

7

Looijenga, E., Rational surfaces with an anti-canonical cycle, Annals of Math., 114(1981), 267-322

8

Masuda, T., On the Rational Solutions of 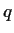$q$-Painlevé V Equation. Nagoya Math. J., at press, preprint nlin.SI/0107050 (2001)

9

Okamoto, K., Sur les feuilletages associés aux équations du second ordre à points critiques fixes de P.Painlevé (French), Japan J. Math., 5(1979), 1-79

10

Ramani, A., Grammaticos, B. and Hietarinta, J., Discrete versions of the Painlevé equations, Phys. Rev. Lett., 67(1991), 1829-1832

11

Sakai, H., Rational surfaces associated with affine root systems and geometry of the Painlevé equations, Commun. Math. Phys., 220(2001) 165-229

12

Takenawa, T., Discrete dynamical systems associated with root systems of indefinite type, Commun. Math. Phys., 224(2001) 657-681