Bibliography

1

M.Jimbo, T.Miwa, K.Ueno : Monodromy preserving deformation of linear ordinary differential equations with rational coefficients I, Physica,2D, 306 - 352 (1981).

2

M.Jimbo, T.Miwa : Monodromy preserving deformation of linear ordinary differential equations with rational coefficients II, Physica,2D, 407 - 448 (1981).

3

H.Kawamuko : Studies on the fourth Painlevé equation in several variables, Ph. D. dissertation, The University of Tokyo, (1997).

4

H.Kawamuko : On the holonomic deformation of linear differential equations, Proc. Japan Acad. Ser. A.,73, 152 - 154 (1997).

5

H.Kawamuko : On the polynomial Hamiltonian structure associated to the 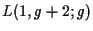$L(1,g+2;g)$ type, Proc. Japan Acad. Ser. A.,73, 155 - 157 (1997).

6

H.Kimura : The degeneration of the two dimensional Garnier system and the polynomial Hamiltonian structure, Ann.Math.Pura.Appl.,155, 25 - 74 (1989).

7

T.Miwa : Painlevé property of monodromy preserving deformation equations and the analyticity of 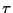$\tau$ functions, Publ. RIMS, Kyoto Univ.,17, 703-721 (1981).

8

Y.Murata : Rational solutions of the second and fourth Painlevé equations, Funk.Ekva.,28, 1 - 32 (1985).

9

K.Okamoto : Studies on the Painlevé equations 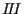$I\!I\!I$, Math.Ann.,275, 221 - 255 (1986).

10

K.Okamoto : The Hamiltonians associated to the Painlevé equations, Pysics. The Painlevé Property, ed. R. Conte, CRM Series in Mathematical Pysics (Springer, 1995), pages 735 - 787.