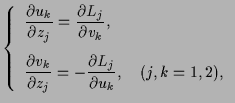 |
(P) |
The present article concerns rational solutions of the fourth Painlevé equation in two variables
=0
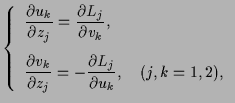 |
(P) |

In [3], we derived a non-linear differential equation in ![]() variables from a holonomic deformation of a certain linear differential equation. When
variables from a holonomic deformation of a certain linear differential equation. When ![]() , this non-linear differential equation is equivalent to the fourth Painlevé equation. The equation (P) corresponds to this non-linear differential equation in
, this non-linear differential equation is equivalent to the fourth Painlevé equation. The equation (P) corresponds to this non-linear differential equation in ![]() . By the general theorey of Miwa [7], it is known that (P) has the Painlevé property. The equation (P) is expected to have many interesting properties as the Painlevé equations in one variable.
. By the general theorey of Miwa [7], it is known that (P) has the Painlevé property. The equation (P) is expected to have many interesting properties as the Painlevé equations in one variable.
In this paper, we find all rational solutions of (P). These rational solutions suggest a symmetry of the transformation group of solutions.