


Next: About this document ...
Up: On uniqueness and existence
Previous: Introduction
- QL
- Qi, J. and Lu, Y., The slowly decaying solutions of
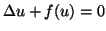 in
in
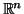 , Funkcialaj Ekvacioj, 41 (1998),
317-326.
, Funkcialaj Ekvacioj, 41 (1998),
317-326.
- SZ
- Serrin, J. and Zou, H., Classification of positive solutions of quasilinear elliptic equations, Topological Methods in
Nonlinear Analysis, 3 (1994), 1-26.
- Pan1
- Pan, X., Existence of singular solutions of semi-linear elliptic equations in
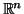 , Journal of Differential Equations, 94 (1991), 191-203
, Journal of Differential Equations, 94 (1991), 191-203
- Pan2
- Pan, X., Positive solutions of
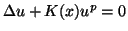 without decay conditions on
without decay conditions on 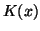 , Proceedings of the American Mathematical Society, 115 (1992), 699-710.
, Proceedings of the American Mathematical Society, 115 (1992), 699-710.
- NS
- Ni, W.-M. and Serrin, J., Nonexistence theorems for singular solutions of quasilinear differential equations, Communications on
Pure and Applied Mathematics, 39
 (1986), 379-399
(1986), 379-399
- LN
- Lin, C.-S. and Ni, W.-M., A counterexample to the nodal domain conjecture and a related semilinear equation, Proceedings of the American Mathematical Society, 102 (1988), 271-277.
- BFP
- Bamón, R. and Flores, I. and del Pino, M., Ground states of semilinear elliptic equations: a geometric approach, Ann. Inst. Henri Poincaré, Analyse non linéaire, 17 (2000), 551-581.
- Ni
- Ni, W.-M., On the elliptic equation
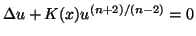 , its gereralizations, and applications in geometry, Indiana University Mathematical Journal, 31 (1982), 493-529.
, its gereralizations, and applications in geometry, Indiana University Mathematical Journal, 31 (1982), 493-529.
- Li
- Li, Y., Asymptotic behavior of positive solutions of equation
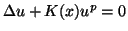 in
in
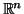 , Journal of Differential Equations, 95 (1992), 304-330.
, Journal of Differential Equations, 95 (1992), 304-330.
Masaaki Maniwa,
Department of Mathematics,
1-1, Minami-Ohsawa, Hachioji-shi,
Tokyo, 192-0397, Japan.
E-mail: mmaniwa@comp.metro-u.ac.jp
Nobuki Takayama
2003-01-30