Theorem 1.1
Suppose that
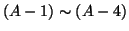
hold. Then any slowly
decaying solution of
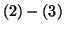
, if it exists, satisfies that for any
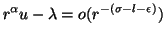 as as  |
(4) |
and there exists at most one slowly decaying solution of
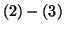
on
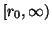
for any
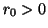
.
Remark 1.1
Theorem 1.1 is an extension of [QL], [SZ]. Actually, in [QL] they asserts existence and uniqueness for more general nonlinearity
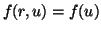
with
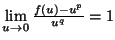
or
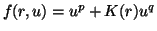
with a bounded function
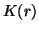
. However, their proof, even for the uniqueness, is based on the higher order asymptotic expansion of slowly decaying solutions. We suspect that such higher order asymptotic expansion can not be obtained if there is an oscillation in the higher order terms of

or
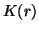
(cf.Theorem 1.2 and 1.3). The method of [QL] cannot be applied for
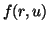
satisfying (A-1)
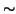
(A-4) in general.
Theorem 1.4
Suppose that (A-1)',(A-2)',(A-3)' hold and
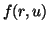
satisfies
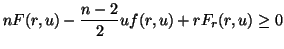 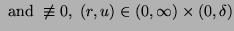 |
(5) |
for any

, where
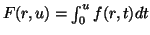
. Then any positive solution of
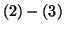
, if it exists on
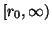
for some
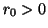
, can be extended to
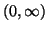
and satisfies
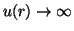 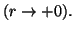 |
(6) |