


Next: Bibliography
Up: Periodic Solutions of Nonlinear
Previous: Periodic Solutions of Nonlinear
In the study of the motions of nonlinear vibrating string with
periodically oscillating ends, it seems to be interesting to investigate
under which conditions periodic motions exist.
In this paper, we shall consider an oscillating string of finite length
in the  -plane.
Let the ends of the string move time-periodically on the
-plane.
Let the ends of the string move time-periodically on the  -plane
and a nonlinear time-periodic vertical external force work on the string.
We shall be concerned with the existence of the time-periodic
motions of the vibrating string under small vertical external forces.
This problem is mathematically formulated as the existence problem of
periodic solutions of the Dirichlet boundary value
problem for one-dimensional wave equation with a time-periodic nonlinear
forcing term, where the boundaries oscillate periodically in
-plane
and a nonlinear time-periodic vertical external force work on the string.
We shall be concerned with the existence of the time-periodic
motions of the vibrating string under small vertical external forces.
This problem is mathematically formulated as the existence problem of
periodic solutions of the Dirichlet boundary value
problem for one-dimensional wave equation with a time-periodic nonlinear
forcing term, where the boundaries oscillate periodically in  on
the
on
the 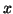 -axis and the ends of the string are forced to move periodically
in
-axis and the ends of the string are forced to move periodically
in  in the vertical direction.
in the vertical direction.
Let 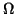 be a time-periodic noncylindrical domain in
be a time-periodic noncylindrical domain in 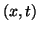 -plane
defined by
-plane
defined by
Here 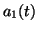 and
and 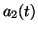 are periodic functions. The period is normalized
to
are periodic functions. The period is normalized
to  , for simplicity.
Consider BVP (the boundary value problem) for a nonlinear one-dimensional
wave equation :
, for simplicity.
Consider BVP (the boundary value problem) for a nonlinear one-dimensional
wave equation :
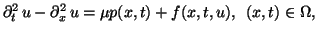 |
(1.1) |
 |
(1.2) |
where 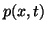 and
and 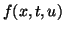 , and
, and
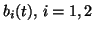 , are periodic
with period
, are periodic
with period  in
in  , and
, and 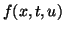 is of order more than or equal to 2
with respect to
is of order more than or equal to 2
with respect to 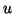 .
. 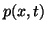 and
and 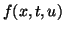 satisfy some compatible boundary
conditions (See (A4) later). As a typical example of
satisfy some compatible boundary
conditions (See (A4) later). As a typical example of 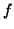 ,
if
,
if
 identically vanish,
then we give
identically vanish,
then we give
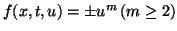 .
. 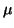 and
and 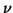 are small parameters and are supposed to satisfy
are small parameters and are supposed to satisfy
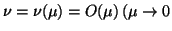 ) continuous in
) continuous in 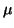 .
The above dependence of
.
The above dependence of 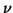 on
on 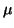 is naturally imposed because we shall
look for the small amplitude solutions and the external force
working the whole string is of
is naturally imposed because we shall
look for the small amplitude solutions and the external force
working the whole string is of
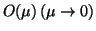 .
We assume that
.
We assume that 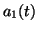 and
and 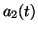 satisfy
satisfy

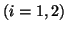 . This condition is natural in the sense that the boundaries
oscillate with slower speed than the eigenspeed
. This condition is natural in the sense that the boundaries
oscillate with slower speed than the eigenspeed  of waves by (1.1).
Otherwise, the shock waves come out.
of waves by (1.1).
Otherwise, the shock waves come out.
The aim of this paper is to show the existence of time-periodic
solutions with small amplitude of BVP (1.1)-(1.2)
with the same period  as that of the given data.
as that of the given data.
We define the following composed function 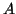 that is a fundamental tool
in this research. Let
that is a fundamental tool
in this research. Let 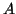 be a composed function defined by
be a composed function defined by
 |
(1.3) |
where 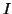 is an identity function,
is an identity function, 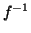 means the inverse function
of
means the inverse function
of 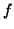 and
and 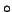 means the composition operation of functions
i.e.
means the composition operation of functions
i.e.
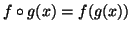 . Geometrically
. Geometrically 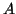 is
a map naturally defined by the reflected characteristics in the
is
a map naturally defined by the reflected characteristics in the 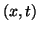 -plane.
-plane.
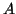 is one dimensional periodic dynamical system. It is known in a series
of works ([Ya1]-[Ya4], [Ya6]) that
is one dimensional periodic dynamical system. It is known in a series
of works ([Ya1]-[Ya4], [Ya6]) that 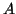 and its rotation number
and its rotation number 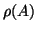 play an essential role in studying the qualitative behavior of solutions
of IBVP and BVP in domain with periodically oscillating boundaries.
For the definition of the rotation number,
see Notation and Definitions in this section.
play an essential role in studying the qualitative behavior of solutions
of IBVP and BVP in domain with periodically oscillating boundaries.
For the definition of the rotation number,
see Notation and Definitions in this section.
For the case where the ends of the string are fixed, BVP is of the form
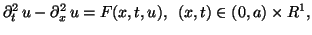 |
(1.4) |
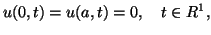 |
(1.5) |
where 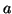 is a positive constant. In this case there are very many works
on the existence of time-periodic solutions of BVP (1.4)-(1.5)
(see [R1][R2][B-C-N][W] etc. and see the references therein).
It should be noted that the ratio of the period of the forcing term
is a positive constant. In this case there are very many works
on the existence of time-periodic solutions of BVP (1.4)-(1.5)
(see [R1][R2][B-C-N][W] etc. and see the references therein).
It should be noted that the ratio of the period of the forcing term
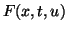 to the length
to the length 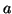 of the interval
of the interval
![$ [\,0,a \,]$](img36.png) plays
an important role in the study of the behavior of the solution.
That is, the behaviors depend on the rationality or irrationality of
the ratio. As is shown in [Ya8], even in the linear case i.e.,
plays
an important role in the study of the behavior of the solution.
That is, the behaviors depend on the rationality or irrationality of
the ratio. As is shown in [Ya8], even in the linear case i.e.,
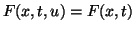 in (1.4) it happens that there are no bounded solutions,
as a matter of course, no periodic solutions of (1.1)-(1.2)
if the Diophantine order of the irrational ratio is large
and the differentiability of
in (1.4) it happens that there are no bounded solutions,
as a matter of course, no periodic solutions of (1.1)-(1.2)
if the Diophantine order of the irrational ratio is large
and the differentiability of 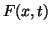 is small. It is known
that if the Diophantine order of a real number is large, the number is
well-approximated by the rational numbers.
is small. It is known
that if the Diophantine order of a real number is large, the number is
well-approximated by the rational numbers.
On the other hand, in our moving-boundary problem (1.1)-(1.2)
the difficulty consists in the following.
The length of the interval
![$ [\,a_1(t),a_2(t)\,]$](img39.png) varies continuously as time
varies continuously. Hence the ratio takes both rational and irrational
values as time proceeds.
However, this difficulty is essentially overcome by introducing the rotation
number of
varies continuously as time
varies continuously. Hence the ratio takes both rational and irrational
values as time proceeds.
However, this difficulty is essentially overcome by introducing the rotation
number of 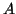 . In a series of papers ([Ya4], [Ya6] and [Ya-Yo])
we clarified the interesting fact that the rotation number plays
the same role as the length of the interval as the ends are fixed.
. In a series of papers ([Ya4], [Ya6] and [Ya-Yo])
we clarified the interesting fact that the rotation number plays
the same role as the length of the interval as the ends are fixed.
We shall show that under the Diophantine condition on the rotation number
(See the assumption (A3) in this section)
there exists a small  -periodic solution of BVP (1.1)-(1.2) (Theorem 1.1).
It is well-known in number theory ([Kh]) that
all real numbers with periodic continued fraction expansions satisfy
the above Diophantine condition.
Especially the set of all algebraic numbers of degree 2 is equal to
the above set.
-periodic solution of BVP (1.1)-(1.2) (Theorem 1.1).
It is well-known in number theory ([Kh]) that
all real numbers with periodic continued fraction expansions satisfy
the above Diophantine condition.
Especially the set of all algebraic numbers of degree 2 is equal to
the above set.
Our steps to show the results on the existence of periodic solutions are
as follows.
First we shall reduce the function 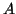 to the affine function,
using the Herman-Yoccoz reduction theorem ([H], [Yoc])
(see Proposition 2.1) :
to the affine function,
using the Herman-Yoccoz reduction theorem ([H], [Yoc])
(see Proposition 2.1) :
Here  is the rotation number of
is the rotation number of 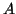 and
and 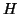 is a conjugate function
that is one-dimensional periodic dynamical system of
is a conjugate function
that is one-dimensional periodic dynamical system of 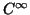 .
Then, using the conjugate function
.
Then, using the conjugate function 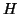 , we shall construct
a domain transformation
, we shall construct
a domain transformation
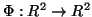 in section 2 :
in section 2 :
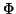 is the bijection of the noncylindrical domain
is the bijection of the noncylindrical domain 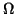 to a cylindrical
domain
to a cylindrical
domain
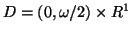 , maps the boundaries of
, maps the boundaries of 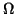 ,
,
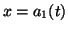 ,
,
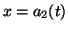 onto the boundaries of
onto the boundaries of  ,
,
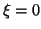 ,
,
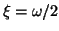 (resp.)
and preserves the d'Alembertian form (Proposition 2.2). The last statement
means that the transformed differential operator contains only d'Alembertian
but has no lower order differential operators.
Such transformations were developped in [Ya4], [Ya6] and [Ya-Yo]. It should
be noted that the above d'Alembertian preserving property has good advantage
to study the qualitative behavior of the solutions. Second, applying
the domain transformation
(resp.)
and preserves the d'Alembertian form (Proposition 2.2). The last statement
means that the transformed differential operator contains only d'Alembertian
but has no lower order differential operators.
Such transformations were developped in [Ya4], [Ya6] and [Ya-Yo]. It should
be noted that the above d'Alembertian preserving property has good advantage
to study the qualitative behavior of the solutions. Second, applying
the domain transformation 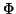 to BVP (1.1)-(1.2), we shall obtain BVP
in the cylindrical domain
to BVP (1.1)-(1.2), we shall obtain BVP
in the cylindrical domain  :
:
 |
(1.6) |
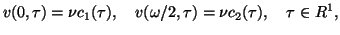 |
(1.7) |
where
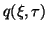 and
and
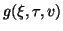 , and
, and
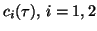 , are
, are
 -periodic in
-periodic in 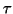 , and
, and
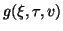 is of order more than or equal
to
is of order more than or equal
to 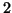 with respect to
with respect to  .
Then we shall show the existence of an
.
Then we shall show the existence of an  -periodic solution of BVP (1.6)-(1.7)
(Theorem 3.1).
In case of
-periodic solution of BVP (1.6)-(1.7)
(Theorem 3.1).
In case of
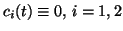 , the problem (1.6)-(1.7) was considered
by [BN-Ma] and [Mc].
Under some monotonicity conditions and the Lipshitz condition on
, the problem (1.6)-(1.7) was considered
by [BN-Ma] and [Mc].
Under some monotonicity conditions and the Lipshitz condition on 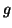 and
the Diophantine condition on the ratio of the length of the interval to
the period of
and
the Diophantine condition on the ratio of the length of the interval to
the period of 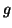 , they showed the existence of periodic weak solution.
, they showed the existence of periodic weak solution.
To show our results, first we shall decompose BVP (1.6)-(1.7)
into two linear homogeneous BVPs
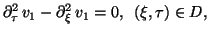 |
(1.8) |
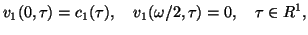 |
(1.9) |
 |
(1.10) |
 |
(1.11) |
and nonlinear BVP
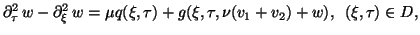 |
(1.12) |
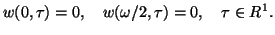 |
(1.13) |
Then we shall show the existence of periodic solutions of BVP (1.8)-(1.9)
and (1.10)-(1.11) (Proposition 3.1), using the method of [Ya3]. In order
to show the existence of a periodic solution of BVP (1.12)-(1.13),
we shall apply the standard contracting mapping principle in suitable function
space to our BVP (1.6)-(1.7).
This is similar to the existence theorem ([Ya5], pp.519-521) of periodic
solutions of nonlinear evolution equations of second order.
Then by the principle of superposition,
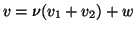 is
the
is
the  -periodic
-periodic 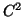 solution of BVP (1.6)-(1.7). Finally,
by operating the inverse
solution of BVP (1.6)-(1.7). Finally,
by operating the inverse 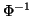 of the domain transformation
of the domain transformation 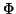 to
the above
to
the above  , we shall obtain the desired
, we shall obtain the desired  -periodic solution of
BVP (1.1)-(1.2).
-periodic solution of
BVP (1.1)-(1.2).
Notation and Definitions.
Rotation Number. Let
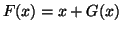 be one dimensional
periodic dynamical system. This means that
be one dimensional
periodic dynamical system. This means that 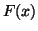 is a continuous monotone
increasing function and
is a continuous monotone
increasing function and  is an
is an  -periodic function. We denote the set
of such functions
-periodic function. We denote the set
of such functions 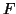 by
by 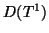 .
.
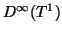 is the subgroup of
is the subgroup of 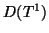 whose elements are of
whose elements are of 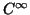 -class.
According to H. Poincaré, the rotation number
-class.
According to H. Poincaré, the rotation number 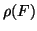 of
of
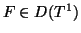 is defined by
is defined by
where 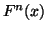 is the
is the 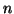 -th iterate of
-th iterate of 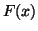 . It is well-known ([H])
that
. It is well-known ([H])
that 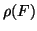 is independent of
is independent of 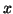 and the convergence is uniform with
respect to
and the convergence is uniform with
respect to 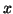 . As we regard
. As we regard 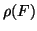 as a functional of
as a functional of 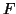 ,
, 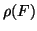 is continuous with respect to
is continuous with respect to
 .
Note that the rotation number has the conjugate-invariant property.
Namely, one has the following identity
for any
.
Note that the rotation number has the conjugate-invariant property.
Namely, one has the following identity
for any
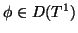 . Since clearly the rotation number
of
. Since clearly the rotation number
of
 (
( : constant) is equal to
: constant) is equal to  ,
it follows that
,
it follows that
 for any
for any
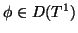 .
For more details of the rotation numbers, see [H].
.
For more details of the rotation numbers, see [H].
Some Function Spaces.
Let 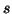 be a nonnegative integer. Let
be a nonnegative integer. Let 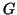 be an open set in
be an open set in 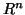 .
Let
.
Let 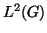 ,
,  and
and 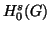 be the usual Lebesgue
space and Sobolev spaces (resp.) with norms
be the usual Lebesgue
space and Sobolev spaces (resp.) with norms
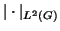 and
and
 .
. 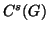 is defined as usual with norm
is defined as usual with norm
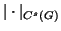 .
We omit
.
We omit 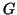 in the norms if there is no confusion. We write
in the norms if there is no confusion. We write
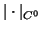 as
as
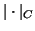 .
.
Let
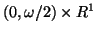 be denoted by
be denoted by  . Let
. Let
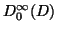 be
a function space whose elements
be
a function space whose elements 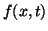 are defined in
are defined in  , of
, of
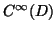 ,
,
 -periodic in
-periodic in  and have the supports contained in
and have the supports contained in  .
We denote a set
.
We denote a set
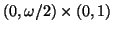 by
by 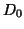 . Let
. Let 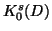 be
the completion of
be
the completion of
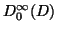 with respect to norm
with respect to norm
 .
We define function spaces
.
We define function spaces
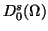 and
and
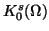 in the same way,
where
in the same way,
where 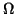 is the noncylindrical domain defined by in section 1.
In this paper, we write
is the noncylindrical domain defined by in section 1.
In this paper, we write 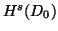 and
and 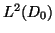 as
as 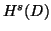 and
and 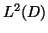 (resp.). All the function spaces
(resp.). All the function spaces 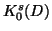 ,
, 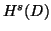 ,
,
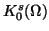 and
and
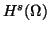 are Hilbert spaces with the above norms.
are Hilbert spaces with the above norms.
Main Theorem
We formulate our main result. Assume the following conditions.
Let 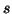 be an integer
be an integer 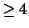 .
.
(A1)
 , are of
, are of 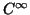 and
and  -periodic,
and satisfy
-periodic,
and satisfy
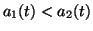 and
and
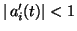 for
for 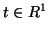 .
.
(A2)
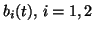 , are of
, are of 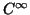 and
and  -periodic.
-periodic.
(A3) The rotation number 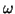 of
of 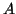 satisfies
the following Diophantine condition : There exists a positive constant
satisfies
the following Diophantine condition : There exists a positive constant
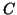 such that
the Diophantine inequality
such that
the Diophantine inequality
holds for all
 .
.
(A4) 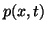 is of
is of 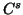 -class with respect to
-class with respect to
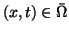 and
and  -periodic in
-periodic in  .
. 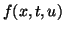 is
of
is
of 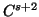 -class with respect to
-class with respect to
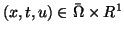 and
and  -periodic in
-periodic in  and satisfies
and satisfies
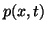 and
and 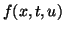 satisfy compatible boundary conditions :
holds for all
satisfy compatible boundary conditions :
holds for all 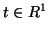 ,
and there exists a positive constant
,
and there exists a positive constant 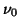 such that for any
such that for any 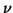 with
with
 ,
holds for all
,
holds for all 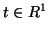 .
.
Remark 1. It is well-known in number theory ([Kh])
that all numbers with periodic continued fraction expansion satisfy (A3).
Note that the set of all algebraic numbers of degree 2 coinsides with
the above set.
Remark 2. 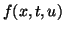 satisfying (A4) is written of the form
satisfying (A4) is written of the form
where  is of
is of 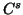 -class with respect to
-class with respect to
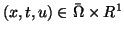 .
As an example of
.
As an example of 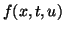 that satisfies the compatible boundary
condition in (A4), we can take
that satisfies the compatible boundary
condition in (A4), we can take  with
with
 ,
for all
,
for all
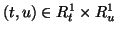 .
. 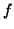 possibly depends on
the parameter
possibly depends on
the parameter 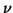 . As such an example we give
. As such an example we give
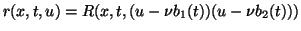 ,
where
,
where 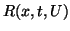 satisfies
satisfies
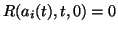 for all
for all 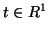 .
.
Remark 3. If 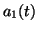 and
and 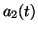 are constants, e.g.
are constants, e.g.
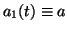 and
and
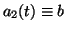 , then we have
, then we have
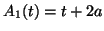 and
and
 , whence
, whence
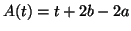 and
and
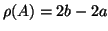 . This
means that
. This
means that 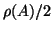 is equal to the length of the interval.
is equal to the length of the interval.
The existence of the boundary functions that satisfy both of
an analytical condition (A1) and a number-theoretic condition (A3) is assured
by the following proposition.
Proposition 1.1
Let
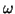
be any real number. Then there exists

-periodic
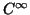
functions

, such that
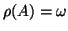
. Here
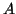
is defined by (1.3).
Proof. Note that the rotation number of
 is
equal to
is
equal to  and the rotation number is conjugate-invariant.
For a given
and the rotation number is conjugate-invariant.
For a given 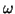 , we define
, we define 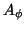 by
by
for
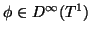 . Then clearly
. Then clearly
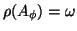 . For simplicity,
we set
. For simplicity,
we set
 . Then
. Then 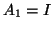 and
and
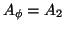 . We set
. We set
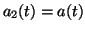 ,
for simplicity. Then by (1.3) we have an equality
where
,
for simplicity. Then by (1.3) we have an equality
where 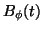 is an 1-periodic
is an 1-periodic  function and satisfy
function and satisfy
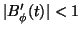 .
Then setting
.
Then setting
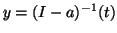 , we have
We consider a function
, we have
We consider a function
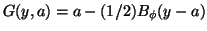 of
of 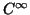 -class
with respect to
-class
with respect to 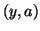 and apply the implicit function theorem to
a functional equation
and apply the implicit function theorem to
a functional equation
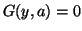 .
Since
.
Since  satisfies
satisfies
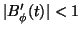 for any
for any 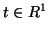 and hence
we have
this functional equation has a
and hence
we have
this functional equation has a 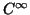 solution
solution 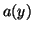 . Q.E.D.
. Q.E.D.
Our main theorem is the following.
Theorem 1.1
Assume (A1), (A2), (A3)
and (A4).
Then there exists a positive constant
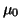
such that for any
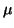
satisfying
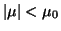
BVP (1.1)-(1.2) has
an

-periodic solution of
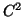
-class with respect to
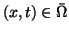
.



Next: Bibliography
Up: Periodic Solutions of Nonlinear
Previous: Periodic Solutions of Nonlinear
Nobuki Takayama
2003-01-30
![]() -plane.
Let the ends of the string move time-periodically on the
-plane.
Let the ends of the string move time-periodically on the ![]() -plane
and a nonlinear time-periodic vertical external force work on the string.
We shall be concerned with the existence of the time-periodic
motions of the vibrating string under small vertical external forces.
This problem is mathematically formulated as the existence problem of
periodic solutions of the Dirichlet boundary value
problem for one-dimensional wave equation with a time-periodic nonlinear
forcing term, where the boundaries oscillate periodically in
-plane
and a nonlinear time-periodic vertical external force work on the string.
We shall be concerned with the existence of the time-periodic
motions of the vibrating string under small vertical external forces.
This problem is mathematically formulated as the existence problem of
periodic solutions of the Dirichlet boundary value
problem for one-dimensional wave equation with a time-periodic nonlinear
forcing term, where the boundaries oscillate periodically in ![]() on
the
on
the ![]() -axis and the ends of the string are forced to move periodically
in
-axis and the ends of the string are forced to move periodically
in ![]() in the vertical direction.
in the vertical direction.
![]() be a time-periodic noncylindrical domain in
be a time-periodic noncylindrical domain in ![]() -plane
defined by
-plane
defined by
![]() as that of the given data.
as that of the given data.
![]() that is a fundamental tool
in this research. Let
that is a fundamental tool
in this research. Let ![]() be a composed function defined by
be a composed function defined by
![]() varies continuously as time
varies continuously. Hence the ratio takes both rational and irrational
values as time proceeds.
However, this difficulty is essentially overcome by introducing the rotation
number of
varies continuously as time
varies continuously. Hence the ratio takes both rational and irrational
values as time proceeds.
However, this difficulty is essentially overcome by introducing the rotation
number of ![]() . In a series of papers ([Ya4], [Ya6] and [Ya-Yo])
we clarified the interesting fact that the rotation number plays
the same role as the length of the interval as the ends are fixed.
. In a series of papers ([Ya4], [Ya6] and [Ya-Yo])
we clarified the interesting fact that the rotation number plays
the same role as the length of the interval as the ends are fixed.
![]() -periodic solution of BVP (1.1)-(1.2) (Theorem 1.1).
It is well-known in number theory ([Kh]) that
all real numbers with periodic continued fraction expansions satisfy
the above Diophantine condition.
Especially the set of all algebraic numbers of degree 2 is equal to
the above set.
-periodic solution of BVP (1.1)-(1.2) (Theorem 1.1).
It is well-known in number theory ([Kh]) that
all real numbers with periodic continued fraction expansions satisfy
the above Diophantine condition.
Especially the set of all algebraic numbers of degree 2 is equal to
the above set.
![]() to the affine function,
using the Herman-Yoccoz reduction theorem ([H], [Yoc])
(see Proposition 2.1) :
to the affine function,
using the Herman-Yoccoz reduction theorem ([H], [Yoc])
(see Proposition 2.1) :
![]() be one dimensional
periodic dynamical system. This means that
be one dimensional
periodic dynamical system. This means that ![]() is a continuous monotone
increasing function and
is a continuous monotone
increasing function and ![]() is an
is an ![]() -periodic function. We denote the set
of such functions
-periodic function. We denote the set
of such functions ![]() by
by ![]() .
.
![]() is the subgroup of
is the subgroup of ![]() whose elements are of
whose elements are of ![]() -class.
According to H. Poincaré, the rotation number
-class.
According to H. Poincaré, the rotation number ![]() of
of
![]() is defined by
is defined by

![]() be a nonnegative integer. Let
be a nonnegative integer. Let ![]() be an open set in
be an open set in ![]() .
Let
.
Let ![]() ,
, ![]() and
and ![]() be the usual Lebesgue
space and Sobolev spaces (resp.) with norms
be the usual Lebesgue
space and Sobolev spaces (resp.) with norms
![]() and
and
![]() .
. ![]() is defined as usual with norm
is defined as usual with norm
![]() .
We omit
.
We omit ![]() in the norms if there is no confusion. We write
in the norms if there is no confusion. We write
![]() as
as
![]() .
.
![]() be denoted by
be denoted by ![]() . Let
. Let
![]() be
a function space whose elements
be
a function space whose elements ![]() are defined in
are defined in ![]() , of
, of
![]() ,
,
![]() -periodic in
-periodic in ![]() and have the supports contained in
and have the supports contained in ![]() .
We denote a set
.
We denote a set
![]() by
by ![]() . Let
. Let ![]() be
the completion of
be
the completion of
![]() with respect to norm
with respect to norm
![]() .
We define function spaces
.
We define function spaces
![]() and
and
![]() in the same way,
where
in the same way,
where ![]() is the noncylindrical domain defined by in section 1.
In this paper, we write
is the noncylindrical domain defined by in section 1.
In this paper, we write ![]() and
and ![]() as
as ![]() and
and ![]() (resp.). All the function spaces
(resp.). All the function spaces ![]() ,
, ![]() ,
,
![]() and
and
![]() are Hilbert spaces with the above norms.
are Hilbert spaces with the above norms.
![]() be an integer
be an integer ![]() .
.
![]() , are of
, are of ![]() and
and ![]() -periodic,
and satisfy
-periodic,
and satisfy
![]() and
and
![]() for
for ![]() .
.
![]() , are of
, are of ![]() and
and ![]() -periodic.
-periodic.
![]() of
of ![]() satisfies
the following Diophantine condition : There exists a positive constant
satisfies
the following Diophantine condition : There exists a positive constant
![]() such that
the Diophantine inequality
such that
the Diophantine inequality
![]() is of
is of ![]() -class with respect to
-class with respect to
![]() and
and ![]() -periodic in
-periodic in ![]() .
. ![]() is
of
is
of ![]() -class with respect to
-class with respect to
![]() and
and ![]() -periodic in
-periodic in ![]() and satisfies
and satisfies
![]() satisfying (A4) is written of the form
satisfying (A4) is written of the form
![]() and
and ![]() are constants, e.g.
are constants, e.g.
![]() and
and
![]() , then we have
, then we have
![]() and
and
![]() , whence
, whence
![]() and
and
![]() . This
means that
. This
means that ![]() is equal to the length of the interval.
is equal to the length of the interval.
![]() is
equal to
is
equal to ![]() and the rotation number is conjugate-invariant.
For a given
and the rotation number is conjugate-invariant.
For a given ![]() , we define
, we define ![]() by
by