


Next: Bibliography
Up: Existence of global solutions
Previous: Existence of global solutions
In this note we consider the existence of global
solution to the initial value problem for the quasilinear wave
equation:
with
where
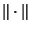 denotes
denotes 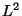 norm in
norm in 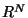 and
and 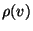 is a differentiable function satisfying
is a differentiable function satisfying
For the Kirchhoff type quasilinear wave equation it is natural to
seek for the solutions in the class
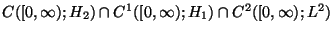 or a little weaker
space
or a little weaker
space
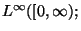
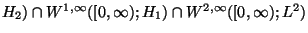 (cf. I. Lasiecka and J.Ong [2]), and we are interested in the global solution of the problem (1.1)-(1.2)
in such a class, ( we often call such a solution as
(cf. I. Lasiecka and J.Ong [2]), and we are interested in the global solution of the problem (1.1)-(1.2)
in such a class, ( we often call such a solution as 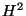 solution).
When
solution).
When 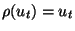 , linear, we see
, linear, we see
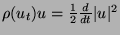 and by use of this fact we can easily
derive the a priori estimates
and by use of this fact we can easily
derive the a priori estimates
and
if
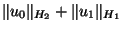 is small.
These a priori estimates are sufficient for the desired global solution.
Indeed, K. Mochizuki [5] has proved such result under a more general condition on the dissipation.
However, the proof heavily depends on the linearity of the dissipation
is small.
These a priori estimates are sufficient for the desired global solution.
Indeed, K. Mochizuki [5] has proved such result under a more general condition on the dissipation.
However, the proof heavily depends on the linearity of the dissipation 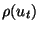 and cannot be applied
to the case of nonlinear dissipation.
Y. Yamada [9] proved the existence of global solutions without direct use of the decay properties.
But in [9] also, the linearity of the dissipation is essentially used.
The object of this note is to prove the existence of global
and cannot be applied
to the case of nonlinear dissipation.
Y. Yamada [9] proved the existence of global solutions without direct use of the decay properties.
But in [9] also, the linearity of the dissipation is essentially used.
The object of this note is to prove the existence of global 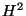 -solution when
-solution when 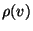 is weakly nonlinear as (1.3), though in our case, solution
is weakly nonlinear as (1.3), though in our case, solution 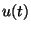 itself belongs to
itself belongs to
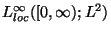 , not
, not
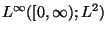 .
Our proof is based on the following observations.
First, we see for an assumed
.
Our proof is based on the following observations.
First, we see for an assumed 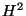 -solution
-solution 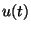 ,
,
where
and hence
Next, differentiating the equation we have
which is rewritten as
with  .
Since
.
Since
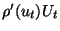 is linear in
is linear in 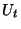 , we can expect the decay estimate
, we can expect the decay estimate
if 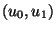 is small. This estimate is weaker than the case
of linear dissipation, but combining this with (1.4) we have a
hope to get desired
is small. This estimate is weaker than the case
of linear dissipation, but combining this with (1.4) we have a
hope to get desired 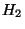 -solutions.
We notice that if the problem is considered in a bounded domain
-solutions.
We notice that if the problem is considered in a bounded domain
 with the boundary condition
with the boundary condition
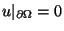 , it
is easy to derive exponential decay
, it
is easy to derive exponential decay
and the global existence of 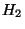 - solution is easily proved.
In fact, more general problem have been treated by many authors (Lasiecka and Ong [2], T. Mizumachi[4], Ono [7,8], Matsuyama and Ikehata [3], Nishihara and Yamada [6] etc.).
But the problem in the whole space
- solution is easily proved.
In fact, more general problem have been treated by many authors (Lasiecka and Ong [2], T. Mizumachi[4], Ono [7,8], Matsuyama and Ikehata [3], Nishihara and Yamada [6] etc.).
But the problem in the whole space 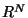 is more delicate because of the lack of Poincaré inequality.
When
is more delicate because of the lack of Poincaré inequality.
When
 , there are proved deep results on global existence and scattering by Yamazaki [10], where Fourier integral method is employed.
, there are proved deep results on global existence and scattering by Yamazaki [10], where Fourier integral method is employed.



Next: Bibliography
Up: Existence of global solutions
Previous: Existence of global solutions
Nobuki Takayama
2003-01-30