


Next: About this document ...
Up: Notes on Space-Time Decay
Previous: Introduction and results
- 1
- Borchers, W. and Miyakawa, T.,
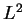 -decay for Navier-Stokes flows
in unbounded domains, with application to exterior stationary flows.
Arch. Rational Mech. Anal. 118 (1992), 273-295.
-decay for Navier-Stokes flows
in unbounded domains, with application to exterior stationary flows.
Arch. Rational Mech. Anal. 118 (1992), 273-295.
- 2
- Brandolese, L., On the localization of symmetric and asymmetric solutions
of the Navier-Stokes equations in
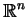 . C. R. Acad. Sci. Paris,
Sér. I Math. 332, No.2 (2001), 125-130.
. C. R. Acad. Sci. Paris,
Sér. I Math. 332, No.2 (2001), 125-130.
- 3
- Fujigaki, Y. and Miyakawa, T., Asymptotic profiles of
nonstationary incompressible Navier-Stokes flows in the whole space.
SIAM J. Math. Anal. 33 (2001), 523-544.
- 4
- Miyakawa, T., On space-time decay properties of nonstationary
incompressible Navier-Stokes flows in
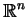 .
Funkcial. Ekvac. 43 (2000), 541-557.
.
Funkcial. Ekvac. 43 (2000), 541-557.
- 5
- Miyakawa, T., Hardy spaces of solenoidal vector fields, with applications
to the Navier-Stokes equations. Kyushu J. Math. 50 (1996), 1-64.
- 6
- Miyakawa, T., On Morrey spaces of measures: basic properties
and potential estimates. Hiroshima Math. J. 20 (1990), 213-222.
- 7
- Miyakawa, T., On upper and lower bounds of rates of decay
for nonstationary Navier-Stokes flows in the whole space.
Preprint, Kobe University, 2001.
- 8
- Miyakawa, T. and Schonbek, M.E., On optimal decay rates
for weak solutions to the Navier-Stokes equations in
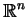 .
Mathematica Bohemica 126 (2001), 443-455.
.
Mathematica Bohemica 126 (2001), 443-455.
- 9
- Takahashi, S., A weighted equation approach to decay rate
estimates for the Navier-Stokes equations. Nonlinear Analysis
37 (1999), 751-789.
Nobuki Takayama
2002-09-18