


Next: Bibliography
Up: Small Data Global Existence
Previous: Small Data Global Existence
Let
 be an exterior domain with compact smooth boundary
be an exterior domain with compact smooth boundary
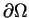 . Without loss of generality we may assume
. Without loss of generality we may assume
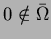 . In this paper we are concerned with the initial-boundary value problem for the linear dissipative wave equation:
. In this paper we are concerned with the initial-boundary value problem for the linear dissipative wave equation:
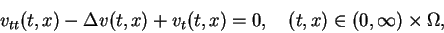 |
(1.1) |
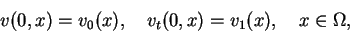 |
(1.2) |
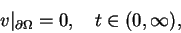 |
(1.3) |
and the semilinear dissipative wave equation:
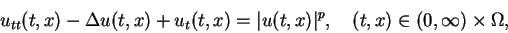 |
(1.4) |
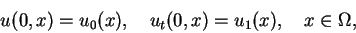 |
(1.5) |
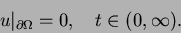 |
(1.6) |
Throughout this paper,
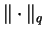 and
and
 mean the usual
mean the usual 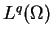 -norm and
-norm and
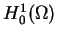 -norm, respectively, and in particular, we set
-norm, respectively, and in particular, we set
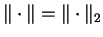 for simplicity. Furthermore, we adopt
for simplicity. Furthermore, we adopt
as the usual 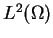 -inner product.
The total energy
-inner product.
The total energy 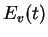 to the equation (1.1) and (1.4) is defined by
to the equation (1.1) and (1.4) is defined by
The first purpose of this job is to derive certain decay estimates for the total energy 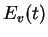 and the
and the 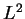 -norm of a solution
-norm of a solution 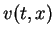 to the linear problem (1.1)-(1.3) faster than the usual one through the (modified) time integral method developed in Ikehata-Matsuyama [3]. In that occasion, we do assume some further restrictions on the initial data as
to the linear problem (1.1)-(1.3) faster than the usual one through the (modified) time integral method developed in Ikehata-Matsuyama [3]. In that occasion, we do assume some further restrictions on the initial data as
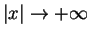 . On the contrary, Ikehata-Matsuyama [3] and Saeki-Ikehata [11] adopted another weight condition on the initial data. For the exterior mixed problem, these restrictions on the initial data seem to be new (for conditions on the initial data with the compact support, see Dan-Shibata [1]). For these restrictions as
. On the contrary, Ikehata-Matsuyama [3] and Saeki-Ikehata [11] adopted another weight condition on the initial data. For the exterior mixed problem, these restrictions on the initial data seem to be new (for conditions on the initial data with the compact support, see Dan-Shibata [1]). For these restrictions as
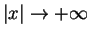 on the initial data to the "Cauchy problem" of the equation (1.1), there are lots of related results and we refer the reader to Kawashima-Nakao-Ono [6], Matsumura [8] and the references thererein.
on the initial data to the "Cauchy problem" of the equation (1.1), there are lots of related results and we refer the reader to Kawashima-Nakao-Ono [6], Matsumura [8] and the references thererein.
The second purpose of this paper is to determine the exponent  of the semilinear exterior problem (1.4)-(1.6) for which the small data global existence property holds. Very recently, in Ikehata-Miyaoka-Nakatake [4] and Todorova-Yordanov [12] they have derived such a critical (Fujita type) exponent
of the semilinear exterior problem (1.4)-(1.6) for which the small data global existence property holds. Very recently, in Ikehata-Miyaoka-Nakatake [4] and Todorova-Yordanov [12] they have derived such a critical (Fujita type) exponent 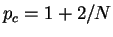 to the Cauchy problem of (1.4) in the framework of
to the Cauchy problem of (1.4) in the framework of
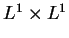 assumption on the initial data and of the initial data with compact support, respectively (for another type of critical exponents like
assumption on the initial data and of the initial data with compact support, respectively (for another type of critical exponents like
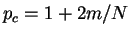 for the Cauchy problem of (1.4) with
for the Cauchy problem of (1.4) with
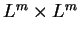 assumption on the initial data, see also Ikehata-Ohta [5]). These works are fully based on the decay estimates for the linear equations due to Matsumura [8] and Kawashima-Nakao-Ono [6]. Thus, it seems to be difficult to apply those decay estimates for the linear equations due to [6] and [8] to the present exterior mixed problem (1.4)-(1.6). On the other hand, in the framework of the compactly supported initial data Ikehata [2] has already constructed a small global solution to the exterior problem (1.4)-(1.6) with the power
assumption on the initial data, see also Ikehata-Ohta [5]). These works are fully based on the decay estimates for the linear equations due to Matsumura [8] and Kawashima-Nakao-Ono [6]. Thus, it seems to be difficult to apply those decay estimates for the linear equations due to [6] and [8] to the present exterior mixed problem (1.4)-(1.6). On the other hand, in the framework of the compactly supported initial data Ikehata [2] has already constructed a small global solution to the exterior problem (1.4)-(1.6) with the power
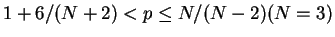 or
or
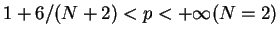 . His result is based on the decay estimates for the linear equations which are developed in [3] and [11]. By using decay estimates for the linear equations developed in the former part instead of those developed in [3] and [11], we can exclude the compactness of the support on the initial data as in [2] to the problem (1.4)-(1.6) with further relaxed exponent, and we can also treat the higher dimensional case
. His result is based on the decay estimates for the linear equations which are developed in [3] and [11]. By using decay estimates for the linear equations developed in the former part instead of those developed in [3] and [11], we can exclude the compactness of the support on the initial data as in [2] to the problem (1.4)-(1.6) with further relaxed exponent, and we can also treat the higher dimensional case 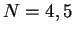 (for another exponent
(for another exponent 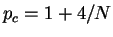 , see Nakao-Ono [10]).
, see Nakao-Ono [10]).
In the following, we set
Then our first result reads as follows.
Theorem 1.1
Let
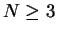
. For each
![$[v_{0},v_{1}] \in (H_{0}^{1}(\Omega)\cap L^{2N/(N+2)}(\Omega))\times (L^{2}(\Omega)\cap L^{2N/(N+2)}(\Omega))$](img33.png)
, the weak solution
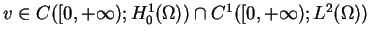
to the linear problem (1.1)-(1.3) satisfies the decay estimates:
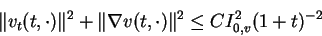 |
(1.7) |
with some generous constant
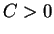
.
Next we shall make some assumptions before treating the semilinear problem (1.4)-(1.6).
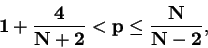 |
(1.8) |
Now based on these decay estimates for the linear equations as in Theorem 1.1 our second result to the semilinear problem reads as follows.
Theorem 1.2
Let
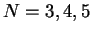
. Under the assumption
(1.8), there exists a real number
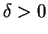
such that if the initial data
![$[u_{0},u_{1}] \in (H_{0}^{1}(\Omega)\cap L^{2N/(N+2)}(\Omega))\times (L^{2}(\Omega)\cap L^{2N/(N+2)}(\Omega))$](img41.png)
further satisfies
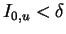
, the problem (1.4)-(1.6) has a unique global solution
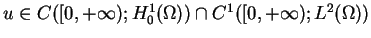
satisfying
with some generous constant
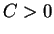
.
Remark 1.1
In the case when
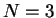
, Theorem 1.2 completely contains the result in Ikehata [
2]. Furthermore, (1.8) is more relaxed condition than that in [
2]. For
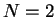
, this is completely open. Note that in the case when
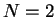
, formally we get
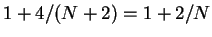
. On the other hand, the results in Theorems 1.1 and 1.2 seem sharp if we take
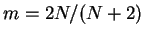
in Ikehata-Ohta [
5, Theorem 1.2]. Finally, for the nonexistence of global solution to the equation (1.4) in

with power

less than the critical exponent we refer to Li-Zhou [
7], Todorova-Yordanov [
12] and Ikehata-Ohta [
5].



Next: Bibliography
Up: Small Data Global Existence
Previous: Small Data Global Existence
Nobuki Takayama
2002-09-18
![]() and
and
![]() mean the usual
mean the usual ![]() -norm and
-norm and
![]() -norm, respectively, and in particular, we set
-norm, respectively, and in particular, we set
![]() for simplicity. Furthermore, we adopt
for simplicity. Furthermore, we adopt
![]() and the
and the ![]() -norm of a solution
-norm of a solution ![]() to the linear problem (1.1)-(1.3) faster than the usual one through the (modified) time integral method developed in Ikehata-Matsuyama [3]. In that occasion, we do assume some further restrictions on the initial data as
to the linear problem (1.1)-(1.3) faster than the usual one through the (modified) time integral method developed in Ikehata-Matsuyama [3]. In that occasion, we do assume some further restrictions on the initial data as
![]() . On the contrary, Ikehata-Matsuyama [3] and Saeki-Ikehata [11] adopted another weight condition on the initial data. For the exterior mixed problem, these restrictions on the initial data seem to be new (for conditions on the initial data with the compact support, see Dan-Shibata [1]). For these restrictions as
. On the contrary, Ikehata-Matsuyama [3] and Saeki-Ikehata [11] adopted another weight condition on the initial data. For the exterior mixed problem, these restrictions on the initial data seem to be new (for conditions on the initial data with the compact support, see Dan-Shibata [1]). For these restrictions as
![]() on the initial data to the "Cauchy problem" of the equation (1.1), there are lots of related results and we refer the reader to Kawashima-Nakao-Ono [6], Matsumura [8] and the references thererein.
on the initial data to the "Cauchy problem" of the equation (1.1), there are lots of related results and we refer the reader to Kawashima-Nakao-Ono [6], Matsumura [8] and the references thererein.
![]() of the semilinear exterior problem (1.4)-(1.6) for which the small data global existence property holds. Very recently, in Ikehata-Miyaoka-Nakatake [4] and Todorova-Yordanov [12] they have derived such a critical (Fujita type) exponent
of the semilinear exterior problem (1.4)-(1.6) for which the small data global existence property holds. Very recently, in Ikehata-Miyaoka-Nakatake [4] and Todorova-Yordanov [12] they have derived such a critical (Fujita type) exponent ![]() to the Cauchy problem of (1.4) in the framework of
to the Cauchy problem of (1.4) in the framework of
![]() assumption on the initial data and of the initial data with compact support, respectively (for another type of critical exponents like
assumption on the initial data and of the initial data with compact support, respectively (for another type of critical exponents like
![]() for the Cauchy problem of (1.4) with
for the Cauchy problem of (1.4) with
![]() assumption on the initial data, see also Ikehata-Ohta [5]). These works are fully based on the decay estimates for the linear equations due to Matsumura [8] and Kawashima-Nakao-Ono [6]. Thus, it seems to be difficult to apply those decay estimates for the linear equations due to [6] and [8] to the present exterior mixed problem (1.4)-(1.6). On the other hand, in the framework of the compactly supported initial data Ikehata [2] has already constructed a small global solution to the exterior problem (1.4)-(1.6) with the power
assumption on the initial data, see also Ikehata-Ohta [5]). These works are fully based on the decay estimates for the linear equations due to Matsumura [8] and Kawashima-Nakao-Ono [6]. Thus, it seems to be difficult to apply those decay estimates for the linear equations due to [6] and [8] to the present exterior mixed problem (1.4)-(1.6). On the other hand, in the framework of the compactly supported initial data Ikehata [2] has already constructed a small global solution to the exterior problem (1.4)-(1.6) with the power
![]() or
or
![]() . His result is based on the decay estimates for the linear equations which are developed in [3] and [11]. By using decay estimates for the linear equations developed in the former part instead of those developed in [3] and [11], we can exclude the compactness of the support on the initial data as in [2] to the problem (1.4)-(1.6) with further relaxed exponent, and we can also treat the higher dimensional case
. His result is based on the decay estimates for the linear equations which are developed in [3] and [11]. By using decay estimates for the linear equations developed in the former part instead of those developed in [3] and [11], we can exclude the compactness of the support on the initial data as in [2] to the problem (1.4)-(1.6) with further relaxed exponent, and we can also treat the higher dimensional case ![]() (for another exponent
(for another exponent ![]() , see Nakao-Ono [10]).
, see Nakao-Ono [10]).