Bibliography

1

Hukuhara, M., I. Meromorfeco de la solvo de (F) 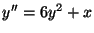$y''=6y^2 + x$, II. Diferenciala sistemo de Schlesinger, III. Ekvivalenteco de la diferenciala sistemo de Schlesinger kaj tiu de Garnier, IV. La ekvacio (VI) de Painlevé-Gambier, unpublished lecture note.

2

Iwasaki, K., Kimura, H., Shimomura, S. and Yoshida, M., From Gauss to Painlevé, Vieweg, 1991.

3

Kac, V.G., Infinite dimensional Lie algebras, 3rd edition, Cambridge Univ. Press, 1990.

4

Matano, T., Matumiya, A. and Takano, K., On some Hamiltonian structures of Painlevé systems II, J. Math. Soc. Japan, 51(1999), 843-766.

5

Matumiya, A., On some Hamiltonian structures of Painlevé systems III, Kumamoto J. Math., 10(1997), 45-73.

6

Noumi, M., Painlevé equations, Asakura Shoten, Tokyo, 2000 (in Japanese).

7

Noumi, M. and Yamada, Y., Affine Weyl groups, discrete dynamical systems and Painlevé equations, Commun. Math. Phys., 199(1998), 281-295.

8

Noumi, M. and Yamada, Y., Symmetries in the fourth Painlevé equation and Okamoto polynomials, Nagoya Math. J., 153(1999), 53-86.

9

Noumi, M. and Yamada, Y., Affine Weyl group symmetries in Painlevé type equations, in Toward the exact WKB analysis of differential equations, linear or non-linear (Eds. C.J. Howl, T. Kawai, Y. Takei), 245-259, Kyoto Univ. Press, Kyoto, 2000.

10

Okamoto, K., Sur les feuilletages associés aux équations du second ordre à points critiques fixes de P. Painlevé, Japan. J. Math., 5(1979), 1-79.

11

Okamoto, K., Studies on the Painlevé equations, I, Ann. Mat. Pura Appl., 146(1987), 337-381; II, Jap. J. Math., 13(1987), 47-76; III, Math. Ann., 275(1986), 221-256; IV, Funkcial. Ekvac., 30 (1987), 305-332.

12

Painalvé, P., Mémoire sur les équations différentielles dont l'integrale generale est uniforme, Bull. Soc. Math. France, 28(1900), 206-261.

13

Painlevé, P., Sur les équations différentielles du second ordre à points critiques fixes, C. R. Acad. Sci. Paris, 143(1906), 1111-1117.

14

Shioda, T. and Takano, K., On some Hamiltonian structures of Painlevé systems I, Funkcial. Ekvac., 40(1997), 271-291.

15

Takano, K., Defining manifolds for Painlevé equations, in Toward the exact WKB analysis of differential equations, linear and nonlinear (Eds. C.J. Howls, T. Kawai and Y. Takei), 261-269, Kyoto Univ. Press, Kyoto, 2000.

16

Watanabe, H., Defining variety and birational canonical transformations of the fifth Painlevé equation, Analysis(Munich), 18(1998), 351-357.

17

Watanabe, H., Defining variety and birational canonical transformations of the fourth Painlevé equation, Funkcial. Ekvac., 42(1999), 1-7.

18

Okamoto, K. and Takano,K., The proof of the Painlevé property by Masuo Hukuhara, Funkcial. Ekvac., 44(2001), 201-217.