Introduction

$\quad\$The purpose of this paper is to show that we can take coordinate systems determined by the Bäcklund transformations as coordinate systems of the manifolds of Painlevé systems constructed by K. Okamoto ([10]) (except the first one) and that the manifolds with parameters equivalent under the corresponding affine Weyl groups are mutually isomorphic.

The $J$-th Painlevé system ( $J=II,III,IV,V,VI$) which is equivalent to the $J$-th Painlevé equation is the following Hamiltonian system

$$\delta q=\{H_J(q,p,t,\alpha),q\}, \quad \delta p=\{H_J(q,p,t,\alpha),p\}, \leqno(H_{J,\alpha})$$

where $\delta=d/dt$ for $J=II,IV$, $\delta=td/dt$ for $J=III,V$, $\delta=t(t-1)d/dt$ for $J=VI$, $\{\cdot, \cdot\}$ is the Poisson bracket defined by

$$\{f,g\}={{\partial f}\over{\partial p}}{{\partial g}\over{\pa... ...{\partial f}\over{\partial q}}{{\partial g}\over{\partial p}},$$

and the Hamiltonian $H_J(q,p,t,\alpha)$, $\alpha=(\alpha_0,\alpha_1,...)$ being parameters with a relation, is given by

$$\begin{eqnarray*} H_{II}(q,p,t,\alpha)&=&{1\over 2}p^2 - (q^2+{t\over 2})p - \a... ... &&(\alpha_0 + \alpha_1 + 2\alpha_2 + \alpha_3 + \alpha_4 = 1). \end{eqnarray*}$$

We notice that the forms of the Hamiltonians for $J=III,IV,V$ given here are slightly different from those in [2],[14],[4]. The Hamiltonian for $J=III$ or $IV$ or $V$ is obtained from that for $J=III'$ or $IV$ or $V$ in [2] respectively by certain change of variables (see Section 3).

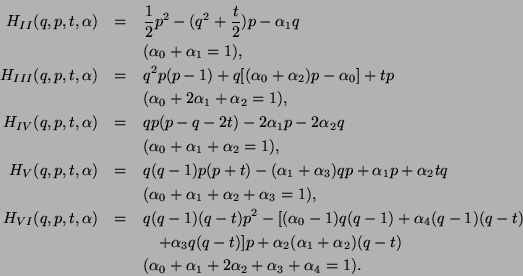
Each Painlevé system determines a complex one dimensional nonsingular foliation of ${\bf C}^2\times B_J(\ni (q,p,t))$ where

$$B_{II}=B_{IV}={\bf C}, \quad B_{III}=B_V={\bf C}-\{0\}, \quad B_{VI}={\bf C}-\{0,1\}.$$

The system is holomorphically extended to one on a manifold $E_{J,\alpha}$ which is a fiber space over $B_J$ having the ${\bf C}^2\times B_J$ as a fiber subspace and the extended system defines a uniform foliation ${\cal F}_{J,\alpha}$ of $E_{J,\alpha}$ although the foliation of the ${\bf C}^2\times B_J$ is not uniform ([14],[4],[10]). Here the uniformity of the foliation ${\cal F}_{J,\alpha}$ means that, for any point $P_0\in E_{J,\alpha}$, every curve in $B_J$ starting from $\pi_J(P_0)$ is lifted on the leaf passing through $P_0$, where $\pi_J$ is the projection from $E_{J,\alpha}$ to $B_J$. We notice that the uniformity of the foliation is equivalent to the so-called Painlevé property for the Painlevé system, that is, if $(q(t),p(t))$ is a local solution of $(H_{J,\alpha})$ determined by an arbitrary initial condition $q(t_0)=q_0\in{\bf C},\ p(t_0)=p_0\in{\bf C}$ with $t_0\in B_J$, then both $q(t)$ and $p(t)$ can be meromorphically continued along any curve in $B_J$ with a starting point $t_0$. The fibers of $E_{J,\alpha}$ are called the spaces of initial conditions([10]). Each $E_{J,\alpha}$ is described by the original chart ${\bf C}^2\times B_J$ and a finite number of copies ${\bf C}^2_i\times B_J$ of ${\bf C}^2\times B_J$ where coordinate transformations are certain birational symplectic ones ([14],[4]).

On the other hand, each Painlevé system admits a Bäcklund transformation group of certain birational symplectic transformations each of which preserves the form of the Hamiltonian and changes the parameters $\alpha_i$ as an element of an affine Weyl group ([6], [7], [8], [9]). This fact was first recognized by K. Okamoto ([11]), but our presentation in the following is different from his.

Let $K={\bf C}(q,p,t,\alpha)$ ( $\alpha=(\alpha_0,\alpha_1,...)$ ) be a differential field of rational functions of $q,p,t,\alpha$ with a derivation $\delta$ defined by

$$\delta f={{\partial f}\over{\partial q}}\cdot\{H_J(q,p,t,\a... ...ial p}}\cdot\{H_J(q,p,t,\alpha),p\} +\delta' f, \quad f\in K,$$

where $\delta'$ is $\partial/\partial t$ for $J=II,IV$, $t\partial/\partial t$ for $J=III,V$, and $t(t-1)\partial/\partial t$ for $J=VI$. (Notice that $\delta \alpha_i =0$.) Then, there is a Bäcklund transformation group $W$ which is a lift of an affine Weyl group acting on the $\alpha$-space such that

(i) each $w\in W$ is an isomorphism from the field $K$ to itself,

(ii) $\delta w = w\delta$, for $w\in W$,

(iii) $w\{f,g\}=\{w(f),w(g)\}$ for $w\in W,\ f,g\in K$.

The group $W$ is generated by a finite number of reflections $s_i$.

For $w\in W$, consider a birational symplectic change of variables from $(q,p,t)$ to $(q_w,p_w,t_w)$ defined by

$$q_w=w(q), \quad p_w=w(p), \quad t_w=w(t).$$

Then the Hamiltonian system ($H_{J,\alpha}$) with $\alpha_0+...=1$ is transformed to ( $H_{J,w(\alpha)}$):

$$\delta q_w=\{H_J(q_w,p_w,t_w,w(\alpha)),q_w\},\ \ \delta p_w=\{H_J(q_w,p_w,t_w,w(\alpha)),p_w\},$$

where $w(\alpha)=(w(\alpha_0),w(\alpha_1),...)$ with $w(\alpha_0)+...=1$. (We notice that $t_w=t$ for every $w\in W$ in the case of $J\not= III$ and $t_w=\pm t$ in the case of $J=III$ and $\delta=\delta_w$ where $\delta_w$ is the derivation with respect to $t_w$.) Hence $w$ extends the domain of definition ${\bf C}^2\times B_J$ of the system ($H_{J,\alpha}$) to ${\bf C}^2\times B_J\sqcup {\bf C}^2_w\times B_{J,w}/\sim$, where $\sim$ is an identification of the points $(q,p,t)\in {\bf C}^2\times B_J$ and $(q_w,p_w,t_w)\in {\bf C}^2_w\times B_{J,w}(\simeq {\bf C}^2\times B_J)$ by the above relation. The system ( $H_{J,w(\alpha)}$) is considered to be the restriction of the extended Hamiltonian system on the chart ${\bf C}^2_w\times B_{J,w}$.

We extend the domain of definition ${\bf C}^2\times B_J$ of ($H_{J,\alpha}$) by all $w\in W$. Let $E^W_{J,\alpha}$ be a manifold obtained by gluing the copies ${\bf C}^2_w\times B_{J,w}, w\in W$ of ${\bf C}^2\times B_J$ via the relations

$$q_{w'}=w'w^{-1}(q_w), \quad p_{w'}=w'w^{-1}(p_w), \quad t_{w'}=w'w^{-1}(t_w)$$

for any $w,w'\in W$ :

$$E^W_{J,\alpha}:=\left(\bigsqcup_{w\in W}{\bf C}^2_w\times B_{J,w}\right) \big/\sim.$$

The identification $\sim$ is well defined since $W$ is a group. We often consider each ${\bf C}^2_w\times B_{J,w}$ a subset of $E^W_{J,\alpha}$.

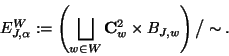
The manifold $E^W_{J,\alpha}$ is a fiber space over $B_J$ and the extension of the Painlevé system ($H_{J,\alpha}$) on $E^W_{J,\alpha}$ defines a complex one dimensional nonsingular foliation of $E^W_{J,\alpha}$ each leaf of which is transversal to fibers.

The main result of this paper is stated as:

Theorem 1. The identity mapping $\phi$ from ${\bf C}^2\times B_J\subset E^W_{J,\alpha}$ to the original chart ${\bf C}^2\times B_J$ of $E_{J,\alpha}$ can be extended to an isomorphism

$$\varphi: \quad E^W_{J,\alpha} \longrightarrow E_{J,\alpha}.$$

In general, for any $w\in W$, the mapping $\phi_w$ from the chart ${\bf C}^2_w\times B_{J,w}\ni (q_w,p_w,t_w)$ of $E^W_{J,\alpha}$ to the original chart ${\bf C}^2\times B_J\ni (q,p,t)$ of $E_{J,w(\alpha)}$ defined by $(q,p,t)=(q_w,p_w,t_w)$ can be extended to an isomorphism

$$\varphi_w: \quad E^W_{J,\alpha} \longrightarrow E_{J,w(\alpha)}.$$

Here an isomorphism means a biholomorphic mapping which preserves fibers and leaves of the foliations.

In the proof of the theorem, the uniformity of the foliation ${\cal F}_{J,\alpha}$ of $E_{J,\alpha}$ plays an essential role. One can find a proof of the uniformity in [15],[18],[1], for example. By means of the theorem, we can say that the manifold $E_{J,\alpha}$ is covered by the coordinate systems ${\bf C}^2_w\times B_{J,w}, w\in W$. The coordinate systems are convenient in that the Hamiltonians on them are easily obtained by the changes of parameters. The following important fact is also an immediate consequence of the theorem.

Corollary. The manifolds $E_{J,\alpha}$ and $E_{J,\alpha'}$ are isomorphic if there exists $w\in W$ such that $\alpha'=w(\alpha)$.

In a private communication, we were informed that H. Umemura and J. Matsuzawa had also obtained the corollary.

We notice that the manifold $E^W_{J,\alpha}$ is covered by a finite number of coordinate systems although it is defined by infinitely many ones. The fact is verified by the above corollary, the following theorem in which $s_i$ are the generators of $W$, and the property that, for any $\alpha$, there is a $w\in W$ such that none of $w(\alpha_i)$ (and $w(\alpha_1+\alpha_2)$ for $J=VI$) vanish. The theorem is also used in the proof of Theorem 1.

Theorem 2. (The case of $J=II,III,IV,V$) If none of $\alpha_i$ vanish, then

$$\left({\bf C}^2\times B_J\bigsqcup\big( \bigsqcup_i{\bf C}^... ...es B_{J,s_i}\big) \right) \big/ \sim \ \ \simeq E_{J,\alpha}.$$

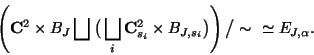
(The case of $J=VI$) If none of $\alpha_i$ and $\alpha_1+\alpha_2$ vanish, then

$$\left({\bf C}^2\times B_{VI}\bigsqcup \big(\bigsqcup_{i=0,... ...1s_2} \times B_{VI}\right)\big/\sim \ \ \simeq E_{VI,\alpha}.$$

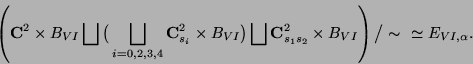
In Section 2, we give lists of certain generators of Bäcklund transformation groups of Painlevé systems and show some propositions which will be used in the proof of Theorem 1. In Section 3, we review the descriptions of the manifolds $E_{J,\alpha}$ ([14],[4]) and give lists of Hamiltonians on all charts and then we show a proposition. The succeeding sections are devoted to proving Theorems 1 and 2. We first prove Theorem 2 in Section 4 and then prove Theorem 1 in Sections 5 and 6. In the case of $J=VI$, there appear divisors in $E^W_{J,\alpha}$ and a divisor in $E_{J,\alpha}$ at infinity of the original chart which are invariant with respect to the foliations, and hence we have to observe them precisely.

In the end of this section, we note a work by H. Watanabe in which he has given some relations between Bäcklund transformations and suitable descriptions of the manifolds ([16], [17]).