


Next: Bibliography
Up: Forced Vibrations of Abstract
Previous: Forced Vibrations of Abstract
In this paper, we investigate the existence of periodic solutions for
certain abstract wave equations. We are motivated by the papers of
K. Ben-Naoum and J. Mawhin [1], and P.J. McKenna [8], where
existence results of periodic solutions are proved for one-dimensional wave
equations when the ratio between the space length and the period
was irrational. Related equations are also studied by M. Yamaguchi in
[10]. We proceeded in this direction in the paper [4]. We
studied the equation
 |
(1) |
where 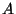 is a self-adjoint, unbounded linear operator with
eigenvalues
is a self-adjoint, unbounded linear operator with
eigenvalues
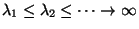 ,
,
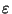 is a small parameter and
is a small parameter and 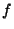 is
is  -periodic in
-periodic in
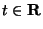 . By a
. By a  -periodic solution of (1) we mean a
weak solution specified below. The following results are proved in
[4] under additional assumptions on
-periodic solution of (1) we mean a
weak solution specified below. The following results are proved in
[4] under additional assumptions on  .
.
Theorem 1
[
4]

Assume there exists a constant

such that
where
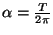
. Then
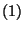
has a weak

-periodic
solution for any
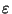
small.
Theorem 2
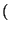
[
4]

Assume
Then the Lebesque measure of the set of all positive
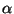
not satisfying
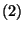
is zero.
We also studied the case when
 . Finally we
considered the example
. Finally we
considered the example
where
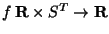 is
is 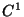 -smooth and
globally Lipschitz in
-smooth and
globally Lipschitz in 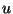 ,
, 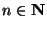 . Here
. Here
![$S^T= {\bf R} /[0,T]$](img28.png) is the
circle. The following result is proved in [4].
is the
circle. The following result is proved in [4].
Theorem 3
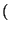
[
4]

The equation
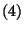
has a weak

-periodic solution, provided that it holds
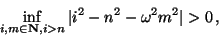 |
(5) |
where

, and there is a
such
that
The purpose of this paper is two-fold. We firstly release the
parameter 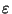 in (1), so we consider the equation
in (1), so we consider the equation
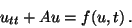 |
(6) |
We have used in [4] the Banach fixed point theorem. To get our
results in this paper, we apply the Leray-Schauder fixed point
theorem. For this reason, we need more precision condition than
(2), see (2.2) below. We also study the resonant case when
 . We derive a Landesman-Lazer type result [7].
Finally, we present a forced beam equation as an example.
. We derive a Landesman-Lazer type result [7].
Finally, we present a forced beam equation as an example.
We secondly investigate more correctly and thoroughly the condition
(5) than in [4]. By using some results of the number theory
[2,3,6], we derive several conditions for  when (5)
is either satisfied or not.
when (5)
is either satisfied or not.



Next: Bibliography
Up: Forced Vibrations of Abstract
Previous: Forced Vibrations of Abstract
Nobuki Takayama
2002-09-18
![]() . Finally we
considered the example
. Finally we
considered the example
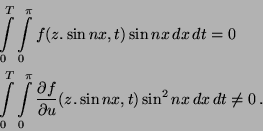
![]() in (1), so we consider the equation
in (1), so we consider the equation
![]() when (5)
is either satisfied or not.
when (5)
is either satisfied or not.