


Next: Bibliography
Up: Convergence of Formal Solutions
Previous: Convergence of Formal Solutions
In [3], H. Chen and H. Tahara studied the following
equation:
|
(1.1) |
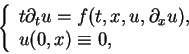 |
where
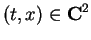 , and
, and 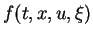 is a
holomorphic function
in a neighbourhood of the origin of
is a
holomorphic function
in a neighbourhood of the origin of
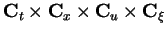 satisfying
satisfying
|
(1.2) |
 |
By the condition (1.2), 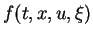 is
written as follows:
is
written as follows:
where 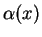 ,
, 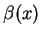 and
and 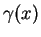 are
holomorphic functions, and
are
holomorphic functions, and
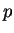 ,
, 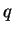 ,
,
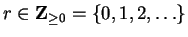 .
.
If
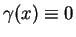 , equation is called of nonlinear
Fuchsian type
(or of Briot-Bouquet type).
In this case, many mathematicians studied the various
theories. For example,
convergence of formal solutions ([4, Chapters 3,5] ),
the Maillet type theorem
([4, Chapter 6] , [7]),
asymptotic expansions ([6]), singular solutions
([4, Chapters 4,5] ).
, equation is called of nonlinear
Fuchsian type
(or of Briot-Bouquet type).
In this case, many mathematicians studied the various
theories. For example,
convergence of formal solutions ([4, Chapters 3,5] ),
the Maillet type theorem
([4, Chapter 6] , [7]),
asymptotic expansions ([6]), singular solutions
([4, Chapters 4,5] ).
If
 and
and
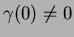 ,
we can see that the equation is solvable in
,
we can see that the equation is solvable in
 .
Therefore, we have a unique holomorphic solution with
arbitrary holomorphic initial data
.
Therefore, we have a unique holomorphic solution with
arbitrary holomorphic initial data
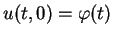 satisfying
satisfying
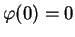 by Cauchy-Kowalevski's theorem, where
by Cauchy-Kowalevski's theorem, where
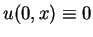 is automatically satisfied.
is automatically satisfied.
In the other case, that is,
 and
and
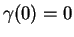 ,
the equation is called of totally characteristic type.
If
,
the equation is called of totally characteristic type.
If
 ,
Chen-Tahara obtained the conditions for the formal
solution to converge ([3]). This result was generalized
to several space
variables by Chen-Luo ([1]) in the case where
,
Chen-Tahara obtained the conditions for the formal
solution to converge ([3]). This result was generalized
to several space
variables by Chen-Luo ([1]) in the case where
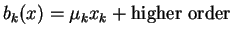 (see (1.4) below), but
(see (1.4) below), but
 variable is still restricted to be one dimensiomal.
variable is still restricted to be one dimensiomal.
If
 ,
Chen-Luo-Tahara proved the
Maillet type theorem, that is, they gave the
formal Gevrey class in which the formal solution
belongs ([2]).
,
Chen-Luo-Tahara proved the
Maillet type theorem, that is, they gave the
formal Gevrey class in which the formal solution
belongs ([2]).
In [3], Chen-Tahara obtained the following result:
Theorem (Chen-Tahara)
Assume (1.2) and that
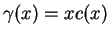 with
with 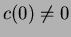 . Then, if
. Then, if
|
(1.3) |
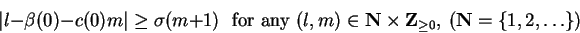 |
holds for some  , then the equation
(1.1) has a unique
holomorphic solution.
, then the equation
(1.1) has a unique
holomorphic solution.
In this paper, we consider a generalization of this
Chen-Tahara's
theorem to the case of several time-space variables.
Let
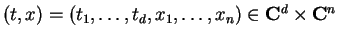 be
be
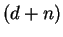 -dimensional complex variables
(
-dimensional complex variables
(
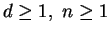 ).
The following
equation seems to be a natural extension of
(1.1)
to several time-space variables:
).
The following
equation seems to be a natural extension of
(1.1)
to several time-space variables:
|
(1.4) |
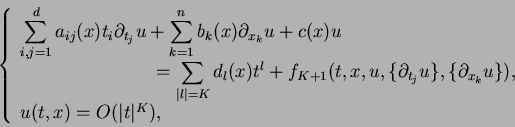 |
where
 ,
,  is a fixed positive
integer satisfying
is a fixed positive
integer satisfying
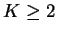 and
and
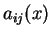 ,
, 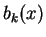 ,
,  and
and 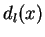 are
holomorphic in a
neighbourhood of the origin, and
are
holomorphic in a
neighbourhood of the origin, and
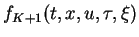
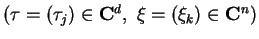 is also holomorphic in a neighbourhood
of the origin with the following Taylor expansion:
is also holomorphic in a neighbourhood
of the origin with the following Taylor expansion:
where 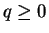 ,
,
 ,
,
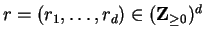 ,
,
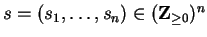 ,
,
and
Here we remark that the assumption 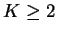 implies
implies
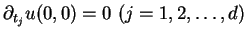 which
assures that
which
assures that
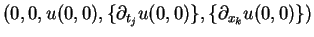 belongs to the domain of definition of
belongs to the domain of definition of
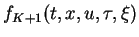 .
.
Now our first theorem is stated as follows:
Theorem 1
Let
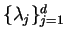
be the eigenvalues of the matrix

.
We assume that
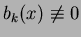
and
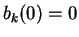
for
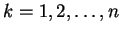
, and let
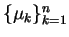
be the eigenvalues of Jacobi matrix of
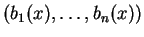
at
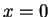
.
Then the formal power series solution of (
1.4)
exists uniquely and converges if the
following conditions are satisfied:
There exists a positive constant 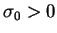 , such that
, such that
|
(1.5) |
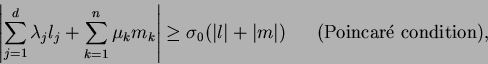 |
and
|
(1.6) |
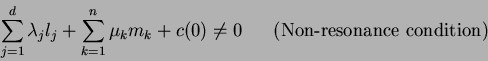 |
hold for all
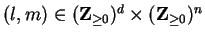
with
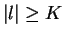
and
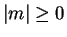
.
Remark 1
It is easy to show the following proposition.
The conditions (1.5) and (1.6)
imply that
|
(1.7) |
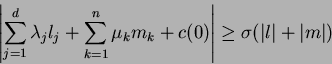 |
holds by some positive constant

for all
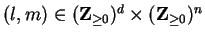
with
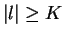
and
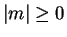
.
In the proof of Theorem
1, this condition
will be used
instead of (
1.5) and (
1.6).
Remark 2
The condition (
1.7)
seems to be stronger than the condition that
|
(1.8) |
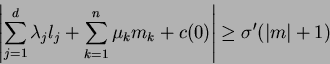 |
holds by some positive constant

for all
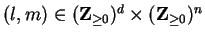
with
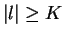
and
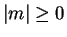
,
which is a direct generalization of Chen-Tahara's
condition (
1.3).
However it is actually proved that
(
1.7) and (
1.8) are equivalent.
The proof can be seen in [
1].
Next, we consider the following general equation:
|
(1.9) |
 |
Assumption 1
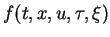
(
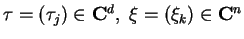
)
is holomorphic in a neighbourhood of the origin, and
is an entire function
in
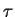
variables for any fixed

,
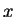
,
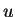
and
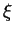
. Moreover we assume that
|
(1.10) |
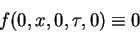 |
for
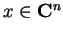
near the origin and
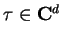
,
which is a generalization of the definition of singular
equations defined in
[
5].
For the equation (1.9), we do not know whether
or not the equation has a
formal solution in general. Therefore, we assume the
following:
Assumption 2
The equation (
1.9) has a formal solution
of the form
|
(1.11) |
![\begin{displaymath}
u(t,x)=\sum_{j=1}^d\varphi_j(x)t_j+\sum_{\vert l\vert\geq2,
\vert m\vert\geq0}u_{lm}t^lx^m\in{\bf C}[[t,x]].
\end{displaymath}](img78.png) |
By the existence of a formal solution,
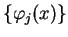 satisfy the following system formally:
satisfy the following system formally:
|
(1.12) |
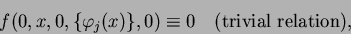 |
and
The formal solution of this system is not convergent
in general. Therefore, we assume
Assumption 3
The coefficients
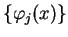
are all
holomorphic in a
neighbourhood of the origin of
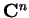
.
Remark 3
In the case
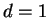
(
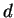
is the dimension of

variables),
a sufficient condition for the formal solution of
(
1.13) to converge has been already obtained
by Miyake-Shirai ([
5]).
In the case
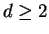
, we give a sufficient condition for
the formal solution of system (
1.13) to be
convergent, which will be given by Theorem 3
in Section 6,
but for a while we consider the problem under
Assumption
3 for simplicity of
our arguments.
Now we put
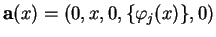 for simplicity, and define
for simplicity, and define
|
(1.14) |
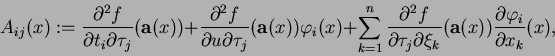 |
for
 . Moreover we define
. Moreover we define
|
(1.15) |
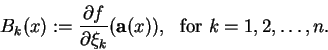 |
Remark 4
The functions
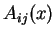
and
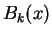
correspond to
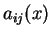
and
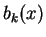
in Theorem 1,
respectively (see (
1.17) below).
Here we assume that the equation is of totally
characteristic type, that is,
Now our second theorem which is our main result
is stated as follows:
Theorem 2
Suppose Assumptions 1, 2, 3 and 4.
Let
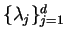
be the eigenvalues of
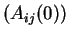
, and let
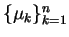
be the eigenvalues of Jacobi
matrix of the vector
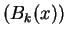
at
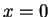
.
Then the formal solution (
1.11) is convergent
if the following condition is satisfied:
There exists a positive constant 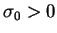 , such
that,
, such
that,
|
(1.16) |
 |
holds for all
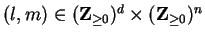
with
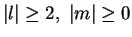
.
Remark 5
Under the assumptions of Theorem 2, if the following
non-resonance condition
holds for all
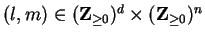
with
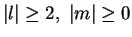
as an additional condition, then the formal power
series solution exists uniquely,
after a determination of
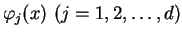
.
Remark 6
By the Poincaré condition, there exists a
positive integer

such that
the non-resonance condition
holds for all
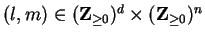
with
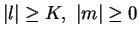
.
We put
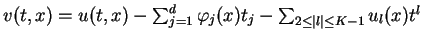 as a new unknown function.
By Assumptions 1, 2, 3 and 4, we can see that
the coefficients
as a new unknown function.
By Assumptions 1, 2, 3 and 4, we can see that
the coefficients
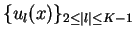 are
determined as holomorphic functions which will be
proved in Appendix B. Moreover,
are
determined as holomorphic functions which will be
proved in Appendix B. Moreover, 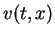 satisfies the
equation of the following form:
satisfies the
equation of the following form:
|
(1.17) |
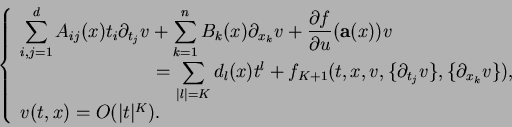 |
This is an equation considered in Theorem 1.
Therefore, it is sufficient to prove Theorem 1
in order to prove Theorem 2.



Next: Bibliography
Up: Convergence of Formal Solutions
Previous: Convergence of Formal Solutions
Nobuki Takayama
2002-09-18
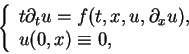
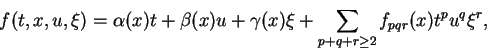
![]() , equation is called of nonlinear
Fuchsian type
(or of Briot-Bouquet type).
In this case, many mathematicians studied the various
theories. For example,
convergence of formal solutions ([4, Chapters 3,5] ),
the Maillet type theorem
([4, Chapter 6] , [7]),
asymptotic expansions ([6]), singular solutions
([4, Chapters 4,5] ).
, equation is called of nonlinear
Fuchsian type
(or of Briot-Bouquet type).
In this case, many mathematicians studied the various
theories. For example,
convergence of formal solutions ([4, Chapters 3,5] ),
the Maillet type theorem
([4, Chapter 6] , [7]),
asymptotic expansions ([6]), singular solutions
([4, Chapters 4,5] ).
![]() and
and
![]() ,
we can see that the equation is solvable in
,
we can see that the equation is solvable in
![]() .
Therefore, we have a unique holomorphic solution with
arbitrary holomorphic initial data
.
Therefore, we have a unique holomorphic solution with
arbitrary holomorphic initial data
![]() satisfying
satisfying
![]() by Cauchy-Kowalevski's theorem, where
by Cauchy-Kowalevski's theorem, where
![]() is automatically satisfied.
is automatically satisfied.
![]() and
and
![]() ,
the equation is called of totally characteristic type.
If
,
the equation is called of totally characteristic type.
If
![]() ,
Chen-Tahara obtained the conditions for the formal
solution to converge ([3]). This result was generalized
to several space
variables by Chen-Luo ([1]) in the case where
,
Chen-Tahara obtained the conditions for the formal
solution to converge ([3]). This result was generalized
to several space
variables by Chen-Luo ([1]) in the case where
![]() (see (1.4) below), but
(see (1.4) below), but
![]() variable is still restricted to be one dimensiomal.
variable is still restricted to be one dimensiomal.
![]() ,
Chen-Luo-Tahara proved the
Maillet type theorem, that is, they gave the
formal Gevrey class in which the formal solution
belongs ([2]).
,
Chen-Luo-Tahara proved the
Maillet type theorem, that is, they gave the
formal Gevrey class in which the formal solution
belongs ([2]).
![]() with
with ![]() . Then, if
. Then, if
![]() be
be
![]() -dimensional complex variables
(
-dimensional complex variables
(
![]() ).
The following
equation seems to be a natural extension of
(1.1)
to several time-space variables:
).
The following
equation seems to be a natural extension of
(1.1)
to several time-space variables:
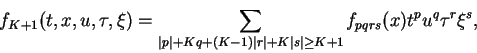
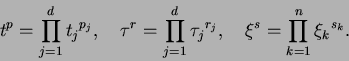
![]() , such that
, such that
![]() satisfy the following system formally:
satisfy the following system formally:
![]() for simplicity, and define
for simplicity, and define
![]() , such
that,
, such
that,
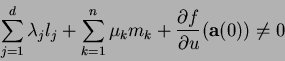
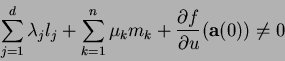
![]() as a new unknown function.
By Assumptions 1, 2, 3 and 4, we can see that
the coefficients
as a new unknown function.
By Assumptions 1, 2, 3 and 4, we can see that
the coefficients
![]() are
determined as holomorphic functions which will be
proved in Appendix B. Moreover,
are
determined as holomorphic functions which will be
proved in Appendix B. Moreover, ![]() satisfies the
equation of the following form:
satisfies the
equation of the following form: