


Next: About this document ...
Up: Molecules of the Hardy
Previous: Introduction
- 1
- Amrouche, C., Girault, Y., Schonbek, M.E. and Schonbek, T.,
Pointwise decay of solutions and of higher derivatives to Navier-Stokes equations, Preprint, UC Santa Cruz (1999).
- 2
- Brandolese, L., personal communication.
- 3
- Brandolese, L., Ecole Normale Supérieure de Cachan, PhD Thesis, work in progress.
- 4
- Carpio, A., Large-time behavior in incompressible Navier-Stokes equations , SIAM J. Math. Anal. 27: 449-475 (1996).
- 5
- Coifman, R.R. and Weiss, G.,Extension of the Hardy spaces and
their use in analysis, Bull. Amer. Math. Soc. 83: 569-645 (1977).
- 6
- Furioli, G., Lemarié-Rieusset P.G. and Terraneo, E.,
Unicité dans
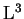 et d'autres espaces limites pour Navier-Stokes, to appear in
Revista Mat. Iberoam.
et d'autres espaces limites pour Navier-Stokes, to appear in
Revista Mat. Iberoam.
- 7
- He, C. and Xin, Z., On the decay properties of solutions to the nonstationary Navier-Stokes equations in
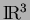 , Preprint, The Chinese University of Hong Kong (1999).
, Preprint, The Chinese University of Hong Kong (1999).
- 8
- Lemarié-Rieusset P.G.,Ondelettes et poids de Muckenhoupt, Studia
Math. 108 (2): 127-147 (1994).
- 9
- Lemarié-Rieusset P.G.,Weak infinite-energy solutions for the
Navier-Stokes equations in
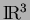 , Université
d'Évry-Val d'Essonne, preprint n.92.
, Université
d'Évry-Val d'Essonne, preprint n.92.
- 10
- Muckenhoupt, B., Weighted norm inequalities for the Hardy
maximal function, Trans. Amer. Math. Soc. 165: 207-226 (1972).
- 11
- May R., Sur l'unicité et la régularité d'une classe de solutions des équations ``mild'' de Navier-Stokes tridimensionnelles, Université d'Évry-Val
d'Essonne, PhD Thesis, work in progress.
- 12
- Miyakawa, T., Hardy spaces of solenoidal vector fields, with applications to the Navier-Stokes equations, Kyushu J. Math. 50: 1-64 (1996).
- 13
- Miyakawa, T., Application of Hardy space techniques to the time-decay problem for incompressible Navier-Stokes flows in
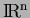 ,
Funkcial. Ekvac. 41: 383-434 (1998).
,
Funkcial. Ekvac. 41: 383-434 (1998).
- 14
- Planchon, F., Solutions globales et comportement asymptotique pour
les équations de Navier-Stokes, PhD Thesis, École Polytechnique (1996).
- 15
- Schonbek, M.E. and Schonbek, T., On the boundedness and decay of moments of solutions of the Navier-Stokes equations, Preprint
CEREMADE, Université de Paris IX, Dauphine (1996).
- 16
- Stein, E.M., Harmonic Analysis. Real-variable methods orthogonality and
oscillatory integrals, Princeton University Press (1993).
- 17
- Takahashi, S., A weighted equation approach to decay rate estimates
for the Navier-Stokes equations, Nonlinear Analysis, 37: 751-789 (1999).
Nuna Adreso
Giulia FURIOLI
Département de Matématiques
Université d'Évry-Val-d'Essonne
Bd. F. Mitterrand
F-91025 EVRY CEDEX
e-mail: giulia@matapp.unimib.it, furioli@lami.univ-evry.fr
and
Elide TERRANEO
Dipartimento di Matematica ``Federigo Enriques''
Università degli studi di Milano
via Saldini, 50
I-20133, MILANO
e-mail: terraneo@balinor.mat.unimi.it,
terraneo@lami.univ-evry.fr
Nobuki Takayama
2002-04-24