Introduction

In this paper we analyze the action of the Navier-Stokes equations on a subspace of $C\left([0,T[,{({\rm L}^3(\rm I\kern-.17em R^3))}^3\right)$ which is specially adapted to study the location and oscillation of the diffusion term $\Delta\vec{u}$. Let us recall the Navier-Stokes system describing the motion of an incompressible, homogeneous, viscous fluid filling out the whole space ${\rm I\kern-.17em R}^3$, without the action of external forces:

$$\left \{ \begin{array}{l} \partial_t\vec{u}= \Delta\vec{u} -... ...{\nabla}p\\ \vec{\nabla}\cdot\vec{u}=0\\ \end{array}\right .$$

where $\vec{u}(t,x):{\rm I\kern-.17em R}^+ \times {\rm I\kern-.17em R}^3\longrightarrow {\rm I\kern-.17em R}^3$ is the velocity vector field and $p(t,x):{\rm I\kern-.17em R}^+ \times {\rm I\kern-.17em R}^3\longrightarrow {\rm I\kern-.17em R}$ is the pressure.

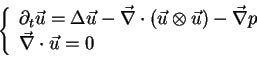
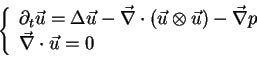
Dealing with the Cauchy problem with initial data $\vec{u}(0,x)=\vec{u}_0(x)$, it is possible to rewrite the system in the following integral expression:

$$\vec{u}(t)= {\rm e}^{t\Delta}\vec{u}_0 - \int_0^t {\rm e}^... ...17em P}\vec{\nabla}\cdot(\vec{u}\otimes\vec{u})(s)ds\leqno (1)$$

where ${\rm e}^{t\Delta}$ is the heat semigroup defined by the convolution with the Gauss kernel:

$${\rm e}^{t\Delta}f(x) = \left ( {1\over (4\pi t)^{3\over 2}}... ...-{\left \vert \cdot \right \vert^2 \over 4t}}\ast f\right )(x)$$

and ${\rm I\kern-.17em P}$ is the projection operator on the divergence-free vector fields, defined by the matrix:

$$\left [ \matrix{ {\rm Id}+R_1R_1 & R_1R_2 & R_1R_3\cr R_2R_1... ...2 & R_2R_3 \cr R_3R_1 & R_3R_2 & {\rm Id}+R_3R_3 \cr} \right ]$$

where $\widehat{R_jf }(\xi)= i{\xi_j\over \left \vert \xi \right \vert}\hat f(\xi)$ are the Riesz transforms for $j=1,2,3$.

In fact the integral and the differential systems are equivalent in this framework, as it is shown in [6] under slight assumptions verified by a large class of spaces.

Given a Banach space $X$, the problem of the existence and the uniqueness of a function $\vec{u}(t) \in C([0,T[,{X}^3)$ solution of (1) in ${\cal S}'$ (a so-called mild solution) is normally approached by a fixed point argument. It is now well known ([6], [11], [9]) that for a given $\vec{u}_0\in ({\rm L}^3(\rm I\kern-.17em R^3))^3$ the only solution in $C\left([0,T[,{({\rm L}^3(\rm I\kern-.17em R^3))}^3\right)$ belongs to every $({{\rm L}^p}({\rm I\kern-.17em R}^3))^3$ space with $p>3$ for all its existence time. We are now interested in investigating the following problem: if the data $\vec{u}_0$ have some extra properties, does the solution keep verifying them at least on a small interval of time?

In [6] it was already established that if $\Delta \vec{u}_0\in ({\cal H}^1)^3$, the Hardy space, then the solution $\vec{u}(t)$ satisfies $\Delta \vec{u}(t)\in ({\cal H}^1)^3$ for $0<t<T'\leq T$. We will consider here a particular case of the previous one where the Laplacian of the data is a ``molecule'' for the Hardy space, and so well-localized in the space variables; we will prove then that the solution verifies the same property, namely its diffusion term keeps on being well-localized at the beginning of the motion.

In the following the reference space will always be ${\rm I\kern-.17em R}^3$.

3=2 3 by 1 3 More precisely, let $\delta\in\ ]{3\over 2}, {9\over 2}[$, $\delta\neq {5\over 2}, {7\over 2}$ and let us introduce the following functional space:

$$X_\delta =\left \{ u\in{\cal S}'\ :\ \begin{array}{l} u\qu... ...} < \delta < { 9\over 2},\ i,j= 1,2,3\\ \end{array}\right \}.$$

The space $X_\delta$ normed by $\left \Vert u \right \Vert _{X_\delta}= \left \Vert \Delta u \right \Vert _{{\rm L}^2((1+\left \vert x \right \vert^{2\delta})dx)}$ is a Banach space.

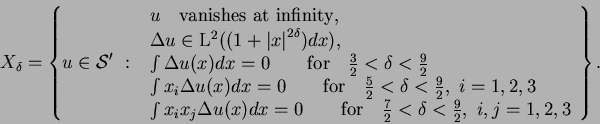
The theorem we are going to prove is the following one.

3=2 3 by 1 3

Theorem .

Let $\vec{u}_0 \in X_\delta^3$ and $\vec{\nabla}\cdot\vec{u}_0=0.$ Then the mild solution of the Navier-Stokes equations $\vec{u}(t) \in C([0,T[,{({{\rm L}^3})}^3)$ is also in $C\left([0,T'],{X_\delta}^3\right)$ for $0<T'\leq T$.

We would like to stress that the solution we obtain decays pointwise in space like ${\displaystyle {1\over 1+\vert x\vert^{\delta-{1\over 2}}}}$ for every $t\in [0,T']$ (see also proposition 2). In the particular case ${3\over 2}<\delta<{7\over 2}$, this decay property may also be recovered by the results of Miyakawa in [12], who establishes a pointwise space-time asymptotic behavior with respect to space-time variables $x$ and $t$ for a particular class of data.

For other results close to these topics see also [1], [3], [4], [7], [13], [15], [17].