Bibliography

1

Burkill, J. and Burkill, H., A Second Course in Mathematical Analysis, Cambridge Univ. Press, p. 53 (1970).

2

CARVALHO, L.A.V. and COOKE, K.L. Collapsible Backward Continuation and Numerical Approximations in a Functional Differential Equation, J.Differential Equations, V. 143 (1998), no. 1, 96-109.

3

FELDSTEIN, A. and GRAFTON, C. Experimental mathematics: an application to retarded ordinary differential equations with infinite time lag, Proc. of the ACM National Conference, pp. 67-71 (1968).

4

FELDSTEIN, A. and ISERLES, A. Embedding of Delay Equations into an Infinite-Dimensional ODE System, Journal of Differential Equations, V.117, No.1, pp.127-150 (1995).

5

FOX, L., MAYERS, D.F., OCKENDON, J.R. and TAYLOR, A.B. On a Functional Differential Equation, J. Inst. Math. Appl., V.8, pp. 271-307 (1971).

6

HALE, J.K. Theory of Functional Differential Equations, Springer-Verlag-Applied Math. Sciences, vol.3 (1977).

7

HÖNIG, C.S. Aplicações da Topologia à Análise (in Portuguese), Projeto Euclides, IMPA, Rio de Janeiro.

8

INCE, E.L. Ordinary Differential Equations, Dover Publications, New York (ND).

9

ISERLES, A. On the generalized pantograph functional-differential equation, Euro. Jnl. of Applied Mathematics, Cambridge University Press, V. 4, pp.1-38, (1993).

10

KATO, T. and McLEOD, J.B. The Functional Differential Equation 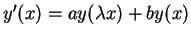$y'(x)=ay(\lambda x)+ by(x)$, Bull. Amer. Math. Soc. V.77 pp. 891-937 (1971).

11

LEIGHTON, W. Ordinary Differential Equations, Wadsworth Publishing Co., Belmont, Ca. (1970).

12

LIMA, E.L. Variedades Diferenciáveis (in Portuguese), IMPA, Rio de Janeiro (1973).

13

LIU, Y.-K. The Linear q-Difference Equation 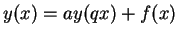$y(x)=ay(qx)+f(x)$, Appl. Math. Lett., V. 8, No.1, pp.15-18 (1995).

14

MAKAY, G. and TERJÉKI, J. On the asymptotic behavior of the pantograph equations(Preprint) Bolyai Institute, Szeged, Hungary (1996).

15

MORRIS, G.L., FELDSTEIN, A. and BOWEN, E.M.The Phragmén-Lindelöf Principle and a Class of Functional Differential Equations, in Ordinary Differential Equations, edited by Leonard Weiss, Academic Press, New York and London, pp.513-540 (1972).

Nuna Adreso

L.A.V. Carvalho

Departamento de Matemática, Universidade Estadual de Maringá
Maringá,

PR, CEP 87020-900, Brazil

K.L.Cooke

Department of Mathematics, Pomona College, Claremont, CA 91711, USA

L.A.C. Ladeira

Departamento de Matemática, ICMSC-USP
São Carlos, SP, CEP 13560-970, Brazil

E-mail: ladeira@icmc.sc.usp.br