


Next: Bibliography
Up: Collapsible Backward Continuation and
Previous: Collapsible Backward Continuation and
We are concerned here with the oscillatory character of certain
solutions of scalar differential equations of the form
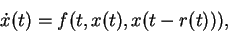 |
(1) |
where 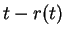 is a given strictly increasing map defined for
is a given strictly increasing map defined for
 for some
for some
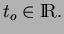 We also assume that
We also assume that 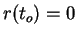 and
and
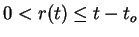 for
for 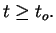 Eq. (1) is a particular
form of a ``retarded differential equation", the delay in time
being provided by the argument
Eq. (1) is a particular
form of a ``retarded differential equation", the delay in time
being provided by the argument 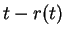 and it is a special kind
of a functional differential equation of the type
and it is a special kind
of a functional differential equation of the type
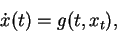 |
(2) |
where 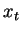 is the ``tail" map (as it is given, for instance, in
[6]),
is the ``tail" map (as it is given, for instance, in
[6]),
![$x_t(\theta)=x(t+\theta),\,\, \theta \in [-r(t),0].$](img10.png) A particular instance of the more general situation to be
investigated in this paper, was studied in [2], namely,
the ``scaled differential equation"
A particular instance of the more general situation to be
investigated in this paper, was studied in [2], namely,
the ``scaled differential equation"
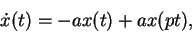 |
(3) |
where 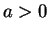 and
and 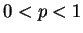 are given real numbers. Here, we have
are given real numbers. Here, we have
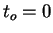 and
and 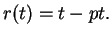 The nomenclature for Eq. (3) is due to
the change of scale in time of the argument
The nomenclature for Eq. (3) is due to
the change of scale in time of the argument 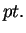 Variations of
this equation have been used in some mathematical models for
pantograph equipment ([3,4,5,9,10,13,14,15]). Eq. (1) has an interesting feature: two different
kinds of initial value problem (IVP) can be attached to it,
namely, the punctual IVP ``
Variations of
this equation have been used in some mathematical models for
pantograph equipment ([3,4,5,9,10,13,14,15]). Eq. (1) has an interesting feature: two different
kinds of initial value problem (IVP) can be attached to it,
namely, the punctual IVP ``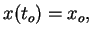 " or the functional IVP
``
" or the functional IVP
``
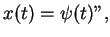 where
where  is arbitrarily chosen in
is arbitrarily chosen in
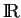 or
or
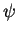 is arbitrarily chosen in
is arbitrarily chosen in
![${\cal C}_\tau=:{\cal C}([\tau',\tau],{\rm I\kern -.2em R}),$](img22.png) and
and 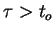 is an arbitrary real constant, with
is an arbitrary real constant, with
 Here, as usual,
Here, as usual,
![${\cal C}([a,b],{\rm I\kern -.2em R})$](img25.png) stands for
the space of the continuous maps from
stands for
the space of the continuous maps from ![$[a,b]$](img26.png) into
into
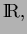 equipped
with the supremum norm
equipped
with the supremum norm
![$\vert\vert\phi\vert\vert=\sup\{\vert\phi(t)\vert:t\in[a,b]\}.$](img28.png) One
often refers to either
One
often refers to either  or
or 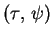 as an
``initial condition". This duality of IVPs directly leads to the
phenomenon of collapse of backward continuation ([2]),
responsible for a wild kind of oscillatory behavior of solutions
of Eq. (1), as we shall see. In order to make notations simpler,
we extend the above nomenclature of
as an
``initial condition". This duality of IVPs directly leads to the
phenomenon of collapse of backward continuation ([2]),
responsible for a wild kind of oscillatory behavior of solutions
of Eq. (1), as we shall see. In order to make notations simpler,
we extend the above nomenclature of 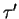 by putting
by putting
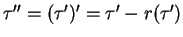 and so on.
and so on.
By a ``solution" of the punctual IVP we mean a differentiable map 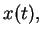 defined in an interval
defined in an interval ![$[t_o,b]$](img34.png) which, of course, satisfies Eq. (1) for
which, of course, satisfies Eq. (1) for ![$t\in [t_o,b]$](img35.png) and
and
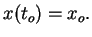 The derivative at
The derivative at 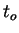 means, of course, the right
hand derivative while the derivative at
means, of course, the right
hand derivative while the derivative at  is the left hand one.
As usual, the notations
is the left hand one.
As usual, the notations  and
and 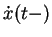 denote the
right-hand and the left-hand derivative of
denote the
right-hand and the left-hand derivative of 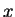 at
at 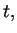 respectively. Similarly, a ``solution" of the functional IVP is a
continuous map
respectively. Similarly, a ``solution" of the functional IVP is a
continuous map
![$x:[\tau',b]\to {\rm I\kern -.2em R},$](img43.png) such that
such that 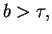
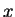 is differentiable in
is differentiable in ![$[\tau,b]$](img45.png) and, of course, satisfies
and, of course, satisfies
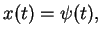
![$t\in [\tau',\tau],$](img47.png)
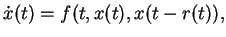
![$t\in[\tau,b]$](img49.png) with the derivative at
with the derivative at  being the right-hand one, etc.. To emphasize the dependence on
being the right-hand one, etc.. To emphasize the dependence on
 and
and 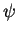 of this solution we shall denote it by
``
of this solution we shall denote it by
``
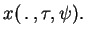 " The solution of the punctual IVP will be
denoted simply by ``
" The solution of the punctual IVP will be
denoted simply by ``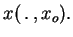 " We assume from now the
following conditions:
" We assume from now the
following conditions:
Hypothesis (H): (i)- 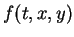 is
continuous in
is
continuous in 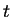 and
and  with respect to
with respect to 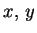 for
for
 (this condition implies that
(this condition implies that
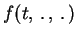 is
locally Lipschitz, i.e., for each compact rectangle
is
locally Lipschitz, i.e., for each compact rectangle
![$Q=[a,b]\times
[c,d]$](img58.png) and
and
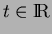 there is a constant
there is a constant  such that
such that
where 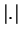 denotes the modulus or absolute value map);
(ii)-
denotes the modulus or absolute value map);
(ii)-
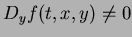 for all
for all
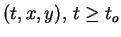 ((ii) implies that
((ii) implies that 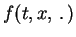 is strictly monotone);
(iii)-
is strictly monotone);
(iii)- 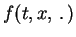 is surjective; (iv)-
is surjective; (iv)-
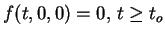 and (v)-
and (v)- 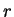 is
is 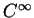 . Assumption (iv)
implies that
. Assumption (iv)
implies that 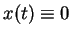 is a solution of Eq. (1), which is
called ``the trivial (or null) solution" and it is the unique
solution for both the punctual IVP ``
is a solution of Eq. (1), which is
called ``the trivial (or null) solution" and it is the unique
solution for both the punctual IVP ``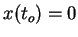 " and the
functional IVP ``
" and the
functional IVP ``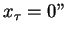 as it will become clear in the
sequel. This equilibrium is denoted by
as it will become clear in the
sequel. This equilibrium is denoted by 
Note that (ii), (iii) and (iv), together, imply that the
sets
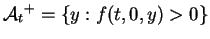 and
and
 are nonempty, disjoint and
are nonempty, disjoint and
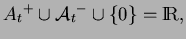
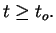 To fix the ideas, we may think, without loss of
generality, that:
To fix the ideas, we may think, without loss of
generality, that:
Hypothesis (G):
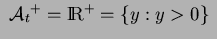 and
and
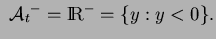
Note that since 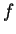 is continuous, it follows that
is continuous, it follows that
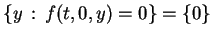 for each
for each 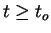 .
.
If we compare the above conditions with the simpler ones in
[2], where the authors made use of the stronger semigroup
property which holds for linear delay equations, we see that the
present conditions are not yet sufficient to guarantee backward
continuation of a large set of initial conditions, as it is
in the linear case. In this paper we use a special property called
piling property to be defined, as well as applications of
implicit function theorems, to extend the results to a much more
general class of problems.



Next: Bibliography
Up: Collapsible Backward Continuation and
Previous: Collapsible Backward Continuation and
Nobuki Takayama
2002-04-24
![]() defined in an interval
defined in an interval ![]() which, of course, satisfies Eq. (1) for
which, of course, satisfies Eq. (1) for ![]() and
and
![]() The derivative at
The derivative at ![]() means, of course, the right
hand derivative while the derivative at
means, of course, the right
hand derivative while the derivative at ![]() is the left hand one.
As usual, the notations
is the left hand one.
As usual, the notations ![]() and
and ![]() denote the
right-hand and the left-hand derivative of
denote the
right-hand and the left-hand derivative of ![]() at
at ![]() respectively. Similarly, a ``solution" of the functional IVP is a
continuous map
respectively. Similarly, a ``solution" of the functional IVP is a
continuous map
![]() such that
such that ![]()
![]() is differentiable in
is differentiable in ![]() and, of course, satisfies
and, of course, satisfies
![]()
![]()
![]()
![]() with the derivative at
with the derivative at ![]() being the right-hand one, etc.. To emphasize the dependence on
being the right-hand one, etc.. To emphasize the dependence on
![]() and
and ![]() of this solution we shall denote it by
``
of this solution we shall denote it by
``
![]() " The solution of the punctual IVP will be
denoted simply by ``
" The solution of the punctual IVP will be
denoted simply by ``![]() " We assume from now the
following conditions:
" We assume from now the
following conditions:
![]() is
continuous in
is
continuous in ![]() and
and ![]() with respect to
with respect to ![]() for
for
![]() (this condition implies that
(this condition implies that
![]() is
locally Lipschitz, i.e., for each compact rectangle
is
locally Lipschitz, i.e., for each compact rectangle
![]() and
and
![]() there is a constant
there is a constant ![]() such that
such that
![]() and
and
![]() are nonempty, disjoint and
are nonempty, disjoint and
![]()
![]() To fix the ideas, we may think, without loss of
generality, that:
To fix the ideas, we may think, without loss of
generality, that:
![]() and
and
![]()
![]() is continuous, it follows that
is continuous, it follows that
![]() for each
for each ![]() .
.