Bibliography

1

D.G.Aronson and Bénilan, Régularité des solutions de l'équation des mileu poreux dans 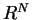$R^{N}$, C. R. Acad. Sci. Paris, Sér. A, 288 (1979), 103-105.

2

P.Bénilan, A strong regularity 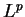$L^{p}$ for solution of the porous media equation, Research Notes in Mathematics Pitman London, 89, 39-58.

3

L.A.Caffarelli and A.Friedman, Regularity of the free boundary of a gas flow in n-dimensional porous medium, Indiana Univ. Math. J., 29 (1980), 361-369.

4

K.Hayasida, On the regularity properties for solutions of the Cauchy problem for the porous media equaion, Proc. Amer. Math. Soc., 107 (1989), 107-112.

4

K.Hayasida, Barenblatt solution and spherically symmetric solution of the porous media equation, Applicable Analysis, 69 (1998), 387-407.

5

A.S.Kalashnikov, Some problem of the qualitative theory of non-linear degenerate second-order parabolic equation, Russian Math. Surveys, 42 (1987), 169-222.

6

O.A.Ladyzhenskaja, V.A.Solonnikov and N.N.Ural'ceva, Linear and quasilinear equations of parabolic type, Transl. Math. Monogr. Amer. Math. Soc. Providence, R.I, 23 (1968).

7

O.A.Oleinik, A.A.Kalashnikov and Chzou Yui-Lin, The Cauchy problem and boundary problems for equations of the type of unsteady filtrations, Izv. Akad. Nauk SSSR, Ser. Math., 22 (1958), 667-704.

8

E.S.Sabinina, On the Cauchy problem for the equation of nonstationary gas filtration in several space variables, Soviet Math., 2 (1961), 166-199.

nuna adreso:
K. Hayasida
Department of Computational Science
Faculty of Science
Kanazawa University
Kanazawa 920-1192
Japan
present address:
Fukui University of Technology
Fukui-City 910-8505
Japan

M.Kobayashi
NEC Communication Systems, LTD
Abiko 270-1198
Japan