


Next: Bibliography
Up: On Regularity for Weak
Previous: On Regularity for Weak
We consider the Cauchy problem for the porous media equation
where 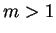 and
and 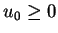 . By a solution of (1.1) we mean a function
. By a solution of (1.1) we mean a function 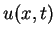 such that
such that
and
for any continuously differentiable function 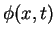 with compact support in
with compact support in
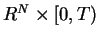 . The problem(1.1) has been studied by many authors. For a detailed account of (1.1) we refer to the survey of Kalashnikov [6]. The existence and the uniqueness of solutions of (1.1) are due to [8] and [9] under some assumption on
. The problem(1.1) has been studied by many authors. For a detailed account of (1.1) we refer to the survey of Kalashnikov [6]. The existence and the uniqueness of solutions of (1.1) are due to [8] and [9] under some assumption on 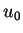 .
.
We are concerned to the regularity property for 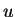 . The local Hölder continuity of
. The local Hölder continuity of 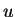 was shown by Caffarelli and Friedman [3]. Aronson and Bénilan [1] proved that
was shown by Caffarelli and Friedman [3]. Aronson and Bénilan [1] proved that
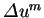 belongs to
belongs to
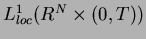 . The method of their proof is to obtain the inequarity
. The method of their proof is to obtain the inequarity
which is in the distribution sence. Soon after Bénilan [2] proved that
if
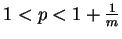 . Here
. Here  needs to be less than 2 in virtue of
needs to be less than 2 in virtue of 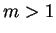 . When
. When 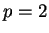 , there is the following result by one of the authors [4]:
, there is the following result by one of the authors [4]:
if
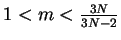 . When
. When 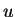 is spherically symmetric under some assumption on
is spherically symmetric under some assumption on 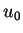 , this result was improved in [5] as follows:
, this result was improved in [5] as follows:
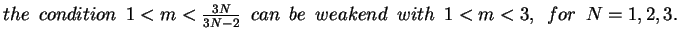
We consider the well-known Barenblatt solution:
where 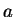 ,
, 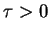 and
and
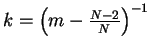 . We rewrite
. We rewrite  simply with
simply with
![$(t+{\tau})^{-k}\left(\left[g\right]_+\right)^{\frac{1}{m-1}}$](img28.png) . Then obviously
. Then obviously
where  and
and 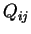 are smooth functions. Hence we see that
are smooth functions. Hence we see that
Let 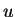 be the spherically symmetric solution of (1.1). Then from the above we conjecture that for any given
be the spherically symmetric solution of (1.1). Then from the above we conjecture that for any given 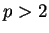
if 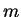 is close to 1. In this paper our first aim is to verify this conjecture (see Theorem 1 ). Secondly we give precisely the admissive value of
is close to 1. In this paper our first aim is to verify this conjecture (see Theorem 1 ). Secondly we give precisely the admissive value of 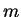 in Theorem 1, when
in Theorem 1, when 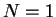 (see Theorem 2). The tool is to prepare some
(see Theorem 2). The tool is to prepare some 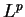 - estimates with a weight by the integreation by parts.
- estimates with a weight by the integreation by parts.



Next: Bibliography
Up: On Regularity for Weak
Previous: On Regularity for Weak
Nobuki Takayama
2002-04-24
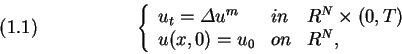
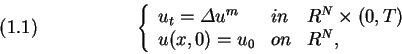
![]() . The local Hölder continuity of
. The local Hölder continuity of ![]() was shown by Caffarelli and Friedman [3]. Aronson and Bénilan [1] proved that
was shown by Caffarelli and Friedman [3]. Aronson and Bénilan [1] proved that
![]() belongs to
belongs to
![]() . The method of their proof is to obtain the inequarity
. The method of their proof is to obtain the inequarity
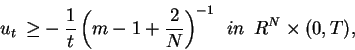
![]()
![\begin{displaymath}w(x,t)=(t+{\tau})^{-k}\left(\left[a^2-\frac{k(m-1)}{2Nm}\frac...
...^2}{(t+{\tau})^{\frac{2k}{N}}}\right]_+\right)^{\frac{1}{m-1}},\end{displaymath}](img23.png)
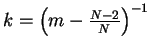 . We rewrite
. We rewrite ![$(t+{\tau})^{-k}\left(\left[g\right]_+\right)^{\frac{1}{m-1}}$](img28.png) . Then obviously
. Then obviously
![]() be the spherically symmetric solution of (1.1). Then from the above we conjecture that for any given
be the spherically symmetric solution of (1.1). Then from the above we conjecture that for any given ![]()