


Next: Bibliography
Up: Structure of positive radial
Previous: Structure of positive radial
The structure of positive radial solutions for nonlinear
elliptic
equations
have attracted much attention for these years. In particular, many
interesting and
beautiful results have been obtained concerning the structure of positive
radial solutions on entire space 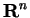 (see, e.g., the survey paper by Ni
[8]). However, it is not straightforward to extend these results
to boundary value problems on bounded domains.
(see, e.g., the survey paper by Ni
[8]). However, it is not straightforward to extend these results
to boundary value problems on bounded domains.
In this paper, we consider the structure of solutions of the semilinear
elliptic equation
|
(1.1) |
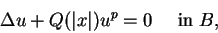 |
where 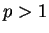 ,
,
 is a given nonnegative function, and
is a given nonnegative function, and
Our main concern is the
existence and uniqueness of positive radial solutions of (1.1)
under the Dirichlet boundary condition
|
(1.2) |
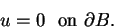 |
Before studying the boundary value problem, we describe the result of
[11] concerning the structure of positive radial solutions of
(1.1) in the entire space 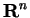 . Since we are concerned with
positive radial solutions, we consider the initial value problem
. Since we are concerned with
positive radial solutions, we consider the initial value problem
|
(1.3) |
 |
Here we assume that 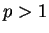 ,
, 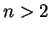 , and
, and 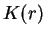 satisfies
satisfies
We note that 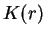 may be unbounded at
may be unbounded at 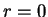 .
Under the first and second conditions, it
is shown in [7,9]
that the initial value problem (1.3) is uniquely solvable if and
only if
.
Under the first and second conditions, it
is shown in [7,9]
that the initial value problem (1.3) is uniquely solvable if and
only if
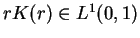 . We denote the unique
solution by
. We denote the unique
solution by 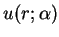 .
It is known [11] that the solution of (1.3) is classified as
.
It is known [11] that the solution of (1.3) is classified as
- a crossing solution:
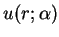 has a zero in
has a zero in
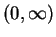 ,
,
- a slowly decaying solution:
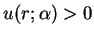 on
on 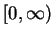 and
and
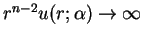 as
as
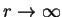 ,
,
- a rapidly decaying solution:
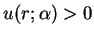 on
on 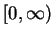 and
and
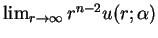 exists and is positive.
exists and is positive.
Finally, it is known [1,6] that if
 ,
then any solution of (1.3) (whether or not it satisfies the initial
condition) cannot be positive near
,
then any solution of (1.3) (whether or not it satisfies the initial
condition) cannot be positive near 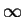 so that
so that 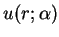 is a
crossing solution for any
is a
crossing solution for any
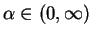 .
.
It is shown in [11] that the Pohozaev identities
|
(1.4) |
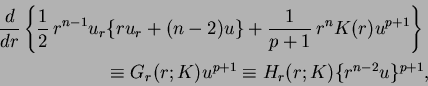 |
play a crucial role for the structure of solution of (1.3), where
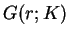 and
and 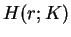 are functions on
are functions on 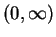 defined by
defined by
respectively.
We define
Here we put  if
if 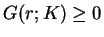 on
on 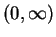 , and
, and
 if
if 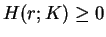 on
on 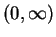 .
.
The following result was obtained in [11].
Theorem A Suppose that (K) holds.
Then the structure of solutions for (1.3) is as
follows:
- (i)
- If
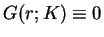 on
on 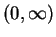 , then the structure is
of Type R:
, then the structure is
of Type R: 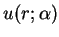 is a rapidly decaying solution for
every
is a rapidly decaying solution for
every 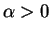 .
.
- (ii)
- Suppose that
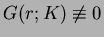 on
on 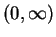 .
.
- (a)
- If
 , then the structure is of
Type C:
, then the structure is of
Type C: 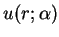 is a crossing solution for every
is a crossing solution for every 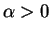 .
.
- (b)
- If
 , then the structure
is of Type S:
, then the structure
is of Type S:
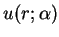 is a slowly decaying solution for every
is a slowly decaying solution for every 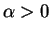 .
.
- (c)
- If
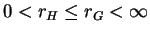 , then the structure is of
Type M: There exists
, then the structure is of
Type M: There exists
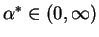 such that
such that
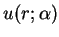 is a
is a
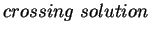 for
for
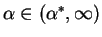 ,
,
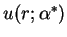 is a rapidly decaying solution, and
is a rapidly decaying solution, and
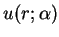 is a slowly decaying solution for
is a slowly decaying solution for
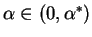 .
.
- (iii)
- Let
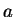 and
and 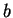 be any given numbers with
be any given numbers with
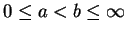 . Then there exists
. Then there exists 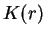 satisfying (K),
satisfying (K),
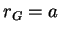 and
and 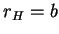 such that the structure is of none of
Types R, C, S, and M.
such that the structure is of none of
Types R, C, S, and M.
Thus, the structure of solutions for (1.3) can be determined
completely in the case  , but cannot be determined from
only
, but cannot be determined from
only 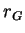 and
and 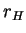 in the case
in the case 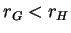 .
We note that
.
We note that
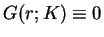 on
on 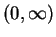 if and only if
if and only if
|
(1.7) |
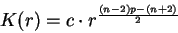 |
for some constant  . In this case, the identity
. In this case, the identity
 holds
on
holds
on 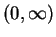 and the solution of (1.3) is explicitly
written as
and the solution of (1.3) is explicitly
written as
|
(1.8) |
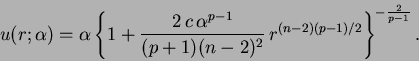 |
The proof of Theorem A in [11] is based on the effective use of the
Pohozaev identities (1.4). Theorem A is a quite
powerful tool to derive
precise information on the structure of solutions, but it was pointed
out by Kwong and Zhang [5] that the method is not
applicable directly to boundary value problems on bounded domains, mainly
because the above Pohozaev identities are not related with the boundary
conditions. Nonetheless, we will show by modifying the method that
similar results can be obtained for the boundary value problems
(see [4] about general results).
Let us return to our original problem (1.1). In order to study
positive radial solutions for the Dirichlet problem (1.1)
with (1.2), we consider the initial value problems
|
(1.9) |
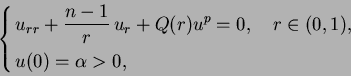 |
and
|
(1.10) |
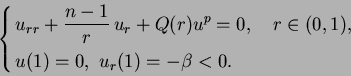 |
For  , we will assume
, we will assume
We note that  may be unbounded at
may be unbounded at 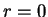 or
or 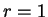 .
As is noted above, under these conditions, (1.9) has a unique solution
.
As is noted above, under these conditions, (1.9) has a unique solution
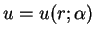 on
on 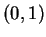 . The last condition in (Q) is a necessary and
sufficient condition on the existence of a unique solution for (1.10)
(see
Lemma 2.7 below). We denote the unique solution by
. The last condition in (Q) is a necessary and
sufficient condition on the existence of a unique solution for (1.10)
(see
Lemma 2.7 below). We denote the unique solution by
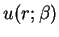 .
.
By Lemma 2.3 given in the next section, the solution of
(1.9) is
classified as
- a crossing solution:
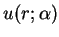 has a zero in
has a zero in 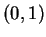 ,
,
- a singular solution:
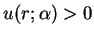 on
on 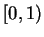 and
and
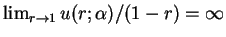 ,
,
- a regular solution:
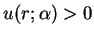 on
on 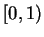 and
and
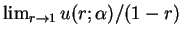 exists and is positive.
exists and is positive.
We will see that if the last condition in (Q) does not hold, then
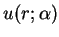 is a crossing solution for any
is a crossing solution for any
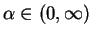 .
We note that depending on
.
We note that depending on  , the singular solution satisfies
, the singular solution satisfies 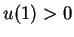 or
or
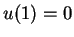 . In the latter case, the singular solution is not differentiable
at
. In the latter case, the singular solution is not differentiable
at
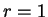 . Thus, if
. Thus, if 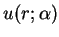 is a regular solution, then
is a regular solution, then
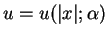 is a solution of
the Dirichlet problem (1.1) with (1.2) in the class
is a solution of
the Dirichlet problem (1.1) with (1.2) in the class
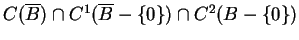 .
.
Similarly, the solution of (1.10) is classified as
- a crossing solution:
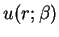 has a zero in
has a zero in 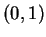 ,
,
- a singular solution:
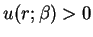 on
on 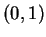 and
and
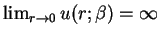 ,
,
- a regular solution:
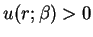 on
on 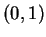 and
and
 exists and is positive.
exists and is positive.
We will see that if the third condition in (Q) does not hold, then
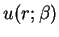 is a crossing solution for any
is a crossing solution for any
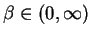 .
Also, if
.
Also, if 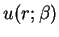 is a regular solution, then
is a regular solution, then
 is a solution of
the Dirichlet problem (1.1) with (1.2) in the class
is a solution of
the Dirichlet problem (1.1) with (1.2) in the class
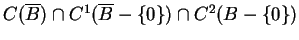 .
.
To derive an analog of Theorem A, we need to modify the Pohozaev
identities and the functions
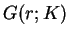 and
and 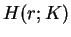 by taking the boundary condition (1.2) into
account. We will see that the following identities are suitable
for our purpose:
by taking the boundary condition (1.2) into
account. We will see that the following identities are suitable
for our purpose:
|
(1.11) |
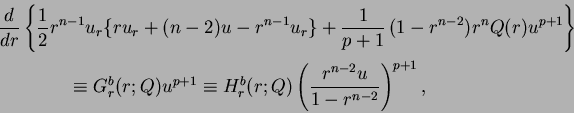 |
where 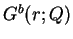 and
and  are functions on
are functions on 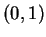 defined by
defined by
We also define
Here we put 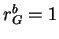 if
if
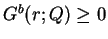 on
on 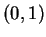 , and
, and
 if
if
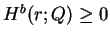 on
on 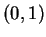 . Thus we have
. Thus we have
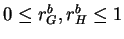 by definition.
by definition.
Now we state our main results
on
(1.9) and (1.10).
Theorem 1.1
Suppose that (Q) holds. Then the structure of solutions
for (
1.9) is as follows:
- (i)
- If
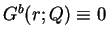 on
on 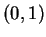 , then the structure is
of Type R:
, then the structure is
of Type R: 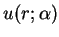 is a regular solution for
every
is a regular solution for
every 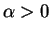 .
.
- (ii)
- Suppose that
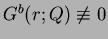 on
on 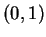 .
.
- (a)
- If
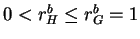 , then the structure is of
Type C:
, then the structure is of
Type C: 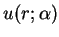 is a crossing solution for every
is a crossing solution for every 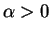 .
.
- (b)
- If
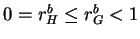 , then the structure is of
Type S:
, then the structure is of
Type S:
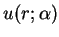 is a singular solution for every
is a singular solution for every 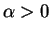 .
.
- (c)
- If
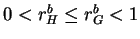 , then the structure is of
Type M: There exists
, then the structure is of
Type M: There exists
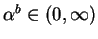 such that
such that
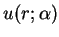 is a
is a
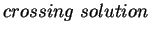 for
for
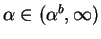 ,
,
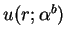 is a regular solution, and
is a regular solution, and
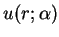 is a singular solution for
is a singular solution for
 .
.
- (iii)
- Let
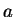 and
and 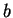 be any given numbers with
be any given numbers with
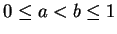 . Then there exists
. Then there exists  satisfying (Q),
satisfying (Q),
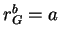 and
and 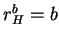 such that the structure is of none of
Types R, C, S, and M.
such that the structure is of none of
Types R, C, S, and M.
Theorem 1.2
Suppose that (Q) holds. Then the structure of solutions
for (
1.10) is as follows:
- (i)
- If
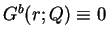 on
on 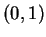 , then the structure is
of Type R:
, then the structure is
of Type R: 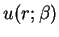 is a regular solution for
every
is a regular solution for
every 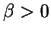 .
.
- (ii)
- Suppose that
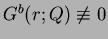 on
on 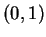 .
.
- (a)
- If
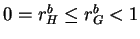 , then the structure is of
Type C:
, then the structure is of
Type C: 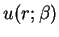 is a crossing solution for every
is a crossing solution for every 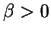 .
.
- (b)
- If
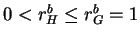 , then the structure is of
Type S:
, then the structure is of
Type S:
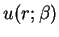 is a singular solution for every
is a singular solution for every 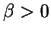 .
.
- (c)
- If
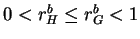 , then the structure is of
Type M: There exists
, then the structure is of
Type M: There exists
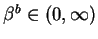 such that
such that
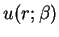 is a
is a
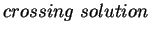 for
for
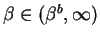 ,
,
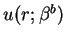 is a regular solution, and
is a regular solution, and
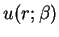 is a singular solution for
is a singular solution for
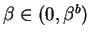 .
.
- (iii)
- Let
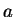 and
and 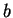 be any given numbers with
be any given numbers with
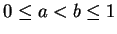 . Then there exists
. Then there exists  satisfying (Q),
satisfying (Q),
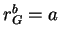 and
and 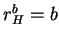 such that the structure is of none of
Types R, C, S, and M.
such that the structure is of none of
Types R, C, S, and M.
We note that
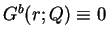 if and only if
if and only if
|
(1.14) |
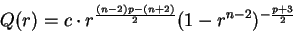 |
for some  . In this case, we have
. In this case, we have
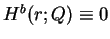 on
on
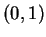 and the solutions of (1.9) and (1.10)
are explicitly written as
and the solutions of (1.9) and (1.10)
are explicitly written as
|
(1.15) |
 |
and
|
(1.16) |
 |
respectively.
There are two ways to prove the above theorems. One is to follow the
proof in [11] for (1.3) by using the modified Pohozaev
identities (1.11). The other is to transform (1.9) and
(1.10) into the form of (1.3) by suitable
changes of variables, and apply Theorem A to the transformed systems.
Then we may inversely transform the results for (1.3) to those
for (1.9) and (1.10). In this paper, we adopt the
latter method.
This paper is organized as follows.
In section 2, we give suitable changes of variables to transform
(1.9) and (1.10) into the form
of (1.3). Then the proofs of Theorems 1.1 and 1.2
are obtained easily from Theorem A.
In section 3, as applications of Theorems 1.1 and 1.2, we give
a few corollaries concerning the structure of solutions for the problems
(1.9) and (1.10) with
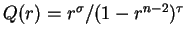 . We will also give an application to some exterior
Dirichlet problem.
Section 4 is devoted to proofs of the corollaries.
. We will also give an application to some exterior
Dirichlet problem.
Section 4 is devoted to proofs of the corollaries.



Next: Bibliography
Up: Structure of positive radial
Previous: Structure of positive radial
Nobuki Takayama
2002-04-24
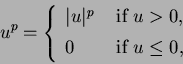
![]() . Since we are concerned with
positive radial solutions, we consider the initial value problem
. Since we are concerned with
positive radial solutions, we consider the initial value problem
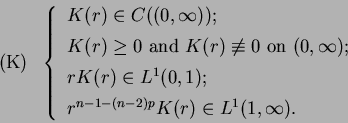

![]() , but cannot be determined from
only
, but cannot be determined from
only ![]() and
and ![]() in the case
in the case ![]() .
We note that
.
We note that
![]() on
on ![]() if and only if
if and only if

![]() and
and ![]() by taking the boundary condition (1.2) into
account. We will see that the following identities are suitable
for our purpose:
by taking the boundary condition (1.2) into
account. We will see that the following identities are suitable
for our purpose:
![]() if and only if
if and only if
![]() . We will also give an application to some exterior
Dirichlet problem.
Section 4 is devoted to proofs of the corollaries.
. We will also give an application to some exterior
Dirichlet problem.
Section 4 is devoted to proofs of the corollaries.